【深度学习】：《100天一起学习PyTorch》第六天：多层感知机（含代码）

【深度学习】：《100天一起学习PyTorch》第六天：多层感知机（含代码）

• ✨本文收录于【深度学习】：《100天一起学习PyTorch》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 个人主页：JoJo的数据分析历险记
• 个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 如果文章对你有帮助，欢迎✌关注、点赞、✌收藏、订阅专栏

参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。

• 视频：动手学深度学习
• 教材：动手学深度学习

写在前面

上一章中介绍了如何使用softmax回归来进行多分类问题，对于一些基本线性模型基本介绍完毕，下面正式进入深度神经网络的学习。先介绍一个比较基础的模型，多层感知机，它是神经网络的最基础模型。首先我们来看看感知机✍

1.感知机

感知机是一个非常简单的处理二分类的模型,首先我们来看看一个简单的例子
对于给定输入$x$，权重$w$,和偏移$b$,感知机输出结果为：
$$f(x)=\{\begin{array}{l}1,wx+b>0\\ -1,wx+b<0\end{array}$$
从这个可以看出如果$y_i(w{x}_i+b)>0$，则分类正确，否则分类错误。因此感知机训练过程为：
$$\begin{gathered} if{y}_i(w{x}_i+b)\le 0 \\ w:=w+y_i{x}_i \\ b:=b+y_i \end{gathered}$$
其中等价于一个梯度下降，其中损失函数为：
$$L=max[0,-y(wx+b)]$$
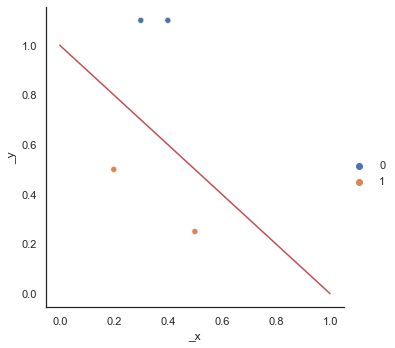
因此感知机的基本思想是找到一个超平面来将两个类别分隔开来，如下图所示

# 导入相关库
import torch
from torch import nn
import matplotlib.pyplot as plt
import seaborn as sns
from torchvision import datasets,transforms
from torch.utils import data
%matplotlib inline

# 创建x,y
x = torch.tensor([[0.5,0.25],[0.2,0.5],[0.3,1.1],[0.4,1.1]])
y = torch.tensor([1,1,0,0])
sns.set(style="white")
sns.relplot(x[:,0],x[:,1],hue=y)
plt.plot([0,1],[1,0],'r')

​

​

上面给出的平面将0,1两类完全分隔开来。但是感知机有一个问题是，解决不了异或问题（XOR），下面我们来介绍一下异或问题

2.异或问题

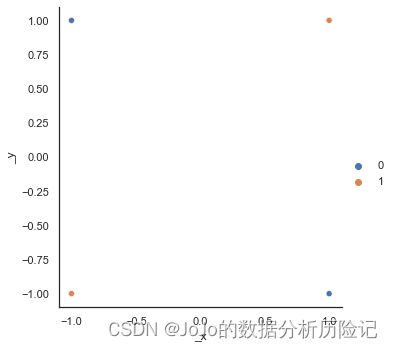
异或问题，当两个相同时，返回正类，不同时，返回负类，具体如下所示

# 创建x,y
x = torch.tensor([[1,1],[-1,1],[-1,-1],[1,-1]])
y = torch.tensor([1,0,1,0])
sns.set(style="white")
sns.relplot(x[:,0],x[:,1],hue=y)

​

可以看出，在这种情况下，无论如何我们没办法找到一个超平面将其分开，这是一组线性不可分的数据，在这种情况下，感知机解决不了异或问题，因此，神经网络的研究暂缓发展。多年之后，提出了多层感知机，自此开起了神经网络的新发展

3多层感知机

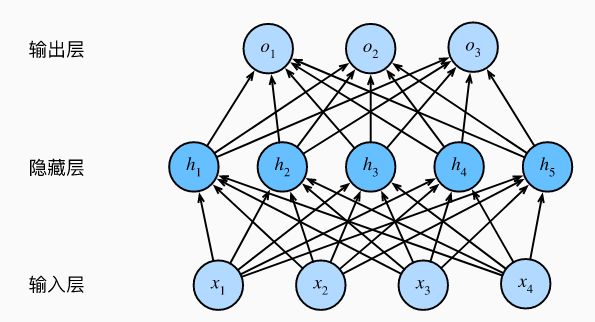
多层感知机通过在网络中加入一个或多个隐藏层来克服线性模型的限制，是一个简单的神经网络，也是深度学习的重要基础，具体如下图所示

这是一个具有一个隐藏层的多层感知机，其中输入有4个特征，输出有三个特征，隐藏层有五个隐藏单元，每一层的权重和偏差维度如下：
$$\begin{gathered} W_{5\times 4}^{[1]},b_{5\times 1}^{[1]} \\ {W}_{3\times 5}^{[2]},b_{3\times 1}^{[2]} \\ ... \\ {W}_{n_{l+1}\times n_l}^{[l]},b_{n_{l+1}}^{[l]} \end{gathered}$$
其中，$n_l$表示第n层神经元的数量。具体计算过程如下：
$$\begin{gathered} Z^{[1]}=W^{[1]}X+b^{[1]} \\ {A}^{[1]}=\sigma (Z^{[1]}) \\ {Z}^{[2]}=W^{[2]}{A}^{[2]}+b^{[2]} \\ {A}^{[2]}=\sigma (Z^{[1]}) \end{gathered}$$
其中$\sigma ()$表示激活函数
每一层的输出是下一个层的输入，直到生成最后的输出

4. 激活函数

如果只是做线性计算的话，那可以转换成一个没有隐藏层的神经网络，因此需要引入激活函数，注意：激活函数必须是非线性的。将激活函数的输出来作为下一层的输入。常用的激活函数可以分为以下几类：

• sigmoid：

$$y=\frac{1}{1+e^{-z}}$$

• tanh

$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}$$

• Relu

$$y=max(0,x)$$

4.1 sigmoid函数

在logistic回归中，我们就运用了sigmoid函数，它能够将输入转换到0-1之间，呈现出S曲线。在处理二分类问题时，可以考虑使用sigmoid函数用于输出层。 具体图形如下

# sigmoid 函数
x = torch.arange(-8.0, 8.0, 0.01, requires_grad=True)
y = torch.sigmoid(x)
plt.ylabel("y = sigmoid(X)")#y标签
plt.grid(True)#显示网格
plt.plot(x.detach(), y.detach())

​

​

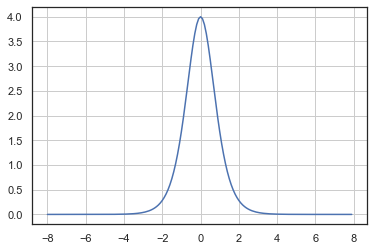
可以看出，当接近0时，变化最大，说明此时导数值最大，对sigmoid函数求导，可得它的导数图如下：

y.backward(torch.ones_like(x),retain_graph=True)
plt.plot(x.detach(), x.grad)

​

​

4.2 Relu激活函数

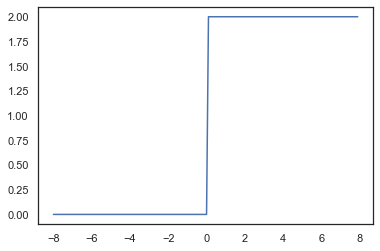
最受欢迎的激活函数是修正线性单元（Rectified linear unit，ReLU）， 因为它实现简单，同时在各种预测任务中表现良好。 ReLU提供了一种非常简单的非线性变换。 给定元素(x)，ReLU函数被定义为该元素与(0)的最大值。因此往往在隐藏层中，我们使用Relu激活函数。其图形如下

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
plt.ylabel("y = Relu(X)")#y标签
plt.grid(True)#显示网格
plt.plot(x.detach(), y.detach())

​

​

可以看出，当输入值为负数，其导数为0，输入值为正时，其导数为1，虽然在0处不可导，但是这种情况一般不会出现，因为输入往往不会为0，下面我们绘制Relu函数的导数

y.backward(torch.ones_like(x),retain_graph=True)
plt.plot(x.detach(), x.grad)

​

​

使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。 这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题，当然还有一些Relu函数的变形

4.3 tanh函数

tanh函数与sigmoid函数类似，将输入压缩到(-1,1)之间。其图形如下

# tanh(x)
y = torch.tanh(x)
plt.ylabel('y=tanh(x)')
plt.grid(True)
plt.plot(x.detach(), y.detach())

​

​

可以看出图形结果和sigmoid函数形状基本一致，唯一有区别的是tanh是关于原点对称的，下面对其进行求导，得到以下结果

# 清除以前的梯度
y.backward(torch.ones_like(x),retain_graph=True)
plt.plot(x.detach(), x.grad)
plt.grid(True)

​

​
求导的结果也和sigmoid函数结果类似。

5.模型训练

• 数据集导入

trans = transforms.ToTensor()
train = datasets.MNIST(root='./data',download=True,train=True,transform=trans)
test = datasets.MNIST(root='./data',download=True,train=False,transform=trans)
# 分批次加载数据集
batch_size = 64
df_train = data.DataLoader(train, batch_size, shuffle=True,
                          )
df_test = data.DataLoader(test, batch_size, shuffle=True,
                           )
X, y = next(iter(df_train))

• 参数初始化

num_in,num_out, num_hid = 784,10,64
W1 = nn.Parameter(
    torch.randn(num_in,num_hid,requires_grad=True))
b1 = nn.Parameter(
    torch.zeros(num_hid,requires_grad = True))
W2 = nn.Parameter(torch.randn(num_hid,num_out,requires_grad=True))
b2 = nn.Parameter(
    torch.zeros(num_out))
params = [W1,b1,W2,b2]

• 定义使用的激活函数

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

• 计算模型

def net(X):
    X = X.reshape((-1, num_in))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

• 损失函数

loss = nn.CrossEntropyLoss(reduction='none')

# SGD优化器
optimizer = torch.optim.SGD(params=params, lr=1)

• 模型训练

for epoch in range(1000):
    optimizer.zero_grad()
    hypothesis = net(X)
    cost = loss(hypothesis, y)
    cost.mean().backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(epoch, cost.mean().item())

0 79.99055480957031
100 0.4515937864780426
200 0.30940207839012146
300 0.25154954195022583
400 0.2046610414981842
500 0.18980586528778076
600 0.1860966980457306
700 0.1445973813533783
800 0.13446013629436493
900 0.09926929324865341

6.简洁代码实现

'''
定义模型
'''
net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 64),
                    nn.ReLU(),
                    nn.Linear(64, 10))
'''
初始化权重
'''
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
'''
损失函数
'''
loss = nn.CrossEntropyLoss()
'''
SGD优化器
'''
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
'''
模型训练
'''
for epoch in range(1000):
    trainer.zero_grad()
    hypothesis = net(X)
    cost = loss(hypothesis, y)
    cost.backward()
    trainer.step()

    if epoch % 100 == 0:
        print(epoch, cost.item())

0 2.2971670627593994
100 0.5922114849090576
200 0.07867014408111572
300 0.028783854097127914
400 0.016159456223249435
500 0.010870776139199734
600 0.008055186830461025
700 0.006334712728857994
800 0.0051856981590390205
900 0.004369326401501894

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！