【动手学深度学习v2】循环神经网络-1.序列模型
文章目录
-
- 1.序列模型
-
- 1.1 统计工具
- 1.2 自回归模型
- 1.3 总结
- 1.4 代码实现-马尔可夫模型回归实现
- 1.5 问题
1.序列模型
与CNN提取空间信息不同的是,序列模型处理的是时间信息。
1.1 统计工具
- 假设在时间t观察到价格 x t x_t xt,那么得到T个不独立的随机变量, p ( x 1 , . . . , x T ) ∼ p ( X ) p(x_1,...,x_T) \sim p(X) p(x1,...,xT)∼p(X)
- 联合概率可以用条件概率展开 p ( a , b ) = p ( a ) p ( b ∣ a ) = p ( b ) p ( a ∣ b ) p(a,b)=p(a)p(b|a)=p(b)p(a|b) p(a,b)=p(a)p(b∣a)=p(b)p(a∣b),由此公式推出 p ( X ) p(X) p(X)的概率,如下图所示:

上图第一个公式为由发生在前面的事件推T时刻的事件 - 为预测 x t x_t xt,我们对条件概率回归, f ( x 1 , . . . , x t − 1 ) f(x_1,...,x_{t-1}) f(x1,...,xt−1)是对见过的数据建模,也称自回归模型。
x t ∼ p ( x t ∣ x 1 , . . . , x t − 1 ) = p ( x t ∣ f ( x 1 , . . . , x t − 1 ) ) (1-1) x_t \sim p(x_t|x_1,...,x_{t-1})=p(x_t|f(x_1,...,x_{t-1})) \tag{1-1} xt∼p(xt∣x1,...,xt−1)=p(xt∣f(x1,...,xt−1))(1-1)
1.2 自回归模型
为有效估计 p ( x t ∣ x 1 , . . . , x t − 1 ) p(x_t|x_1,...,x_{t-1}) p(xt∣x1,...,xt−1),有以下两种方案:
方案A-马尔可夫模型
为了估计 x t x_t xt,有时候使用t时刻之前所有序列作为观测序列是不必要的,往往与t时刻的时间跨度太大的时刻已经影响不了t时刻的值 x t x_t xt,因此我们只需要满足某个长度为 τ \tau τ的时间跨度, 即使用观测序列 x t − 1 , . . . , x t − τ x_{t-1},...,x_{t-\tau} xt−1,...,xt−τ即可。只要这种是近似精确的,我们就说序列满足马尔可夫条件(Markov condition)。马尔可夫条件只需要考虑过去观察中的一个非常短的时间段。
方案B-潜变量模型
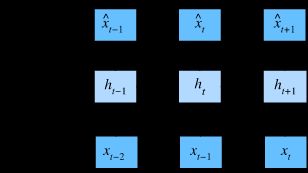
潜变量模型保留了一部分过去的观测总结 h t h_t ht, h t = f ( x 1 , . . . , x t − 1 ) h_t=f(x_1,...,x_{t-1}) ht=f(x1,...,xt−1),从而可以基于 x ^ = p ( x t ∣ h t ) \hat{x}=p(x_t|h_t) x^=p(xt∣ht)估计 x t x_t xt,这类模型也被称为隐变量自回归模型。

模型一: h ′ h^{'} h′与前一个时刻的观测总结(潜变量) h h h和前一个 x x x值相关。
模型二: x ′ x^{'} x′由 h ′ h^{'} h′和前一个时刻的 x x x值估计。
1.3 总结
- 时序模型中,当前数据跟之前观察到的数据相关
- 自回归模型使用自身过去数据来预测未来
- 马尔科夫模型假设当前只跟当前少数数据相关,每次都使用固定长度的过去信息来预测现在,从而简化模型
- 潜变量模型使用潜变量来概括历史信息,使得模型拆分成两块:一块是根据现在观测到的数据来更新潜变量;另一块是根据更新后的潜变量和过去的数据来更新将来要观测到的数据
- 对于时间是向前推进的因果模型,正向估计通常比反向估计更容易
- t时刻的观测值对t+i的估计中,i值越大,积累的误差也就越大
1.4 代码实现-马尔可夫模型回归实现
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
T = 1000 # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
# 使用正弦函数和一些可加性噪声来生成序列数据
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
# 使用马尔可夫模型,tau取4
tau = 4
# 由于没有足够的历史记录来描述前tau个数据样本,因此这里训练集只有T-tau个,每个训练样本取该时刻前tau个观测值
features = torch.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i: T - tau + i]
# 标签
labels = x[tau:].reshape((-1, 1))
batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
# 初始化网络权重的函数
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
# 一个简单的多层感知机
def get_net():
net = nn.Sequential(nn.Linear(4, 10),
nn.ReLU(),
nn.Linear(10, 1))
net.apply(init_weights)
return net
# 平方损失。注意:MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')
# 将马尔可夫模型转换为回归问题
# 训练
def train(net, train_iter, loss, epochs, lr):
trainer = tf.keras.optimizers.Adam()
for epoch in range(epochs):
for X, y in train_iter:
with tf.GradientTape() as g:
out = net(X)
l = loss(y, out)
params = net.trainable_variables
grads = g.gradient(l, params)
trainer.apply_gradients(zip(grads, params))
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)
epoch 1, loss: 0.602395
epoch 2, loss: 0.364904
epoch 3, loss: 0.248402
epoch 4, loss: 0.173626
epoch 5, loss: 0.120276
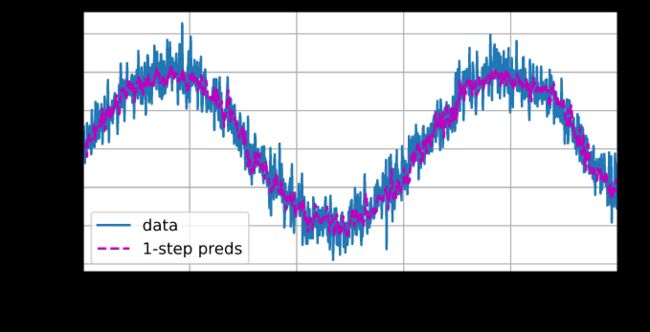
预测
当给出t=600后的每个的观测值x,预测效果不错,如果数据观察序列的时间步只到604,比如时间步为608的预测样本为前面4个时刻预测的值,而不是取变量x中的值,效果可能就会非常差。
onestep_preds = net(features)
d2l.plot([time, time[tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000],
figsize=(6, 3))
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
multistep_preds[i] = net(
multistep_preds[i - tau:i].reshape((1, -1)))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))

绿线的预测显然并不理想,是因为误差会随着时间呈线性增加而逐渐累积,导致预测结果偏移理想结果。
1.5 问题
1、这里的图和公式是不是不一致,公式的 x 只和 h 相关,而图里 x 和 h 以及 x(t-1) 相关
2、老师,潜变量是不是直接影响了 RNN 的创造,或者说 RNN 的隐单元也是一个潜变量单元
3、在常规范围内 τ 是不是越大越好,刚才例子 τ = 5 是不是比4好?
4、潜变量模型和隐马尔科夫模型有什么区别?
5、老师,若预测一个月,τ = 30;若预测 7 天,τ = 7,是否有这样的关系,还是有其它的约定规则?
6、图上看这里当前环境的影响只能从过去来吗?感觉还可以加一个当前环境因素
7、在预测未来方面,现在的 SOTA 模型能做到多好?
8、可不可以认为是 MLP 记住了过去数据的模式?然后去用这个模式去画出未来的趋势?
9、请问老师这里输入特征和输出关系是具体如何应对的?输入 feature.shape(T-tau,tau),但是每一列时间都错开一个时间。输出 label 是从 tau:T.这里每一列的 feature 和我们的 label 的对应关系都在改变
10、τ 能够随着 xt 的变化而变化吗?这样感觉更符合实际情况,比如 xt 与前 5 个变量相关,x(t+1) 与前 6 个变量相关
11、发动机或者电动车电池上面有很多参数传感器,在预测这些参数未来变化趋势时,采用马尔科夫模型进行单步预测还可以,但是长步预测结果极差。请问有其他的好办法吗?
12、模型能学习多个连续输入,比如 a 、 b 、 c ,以及他们之间的联系吗?
13、李沐老师好!时间序列函数,有一个很著名的例子,第谷观测的太阳系行星位置观测数据。这个数据集是否是整理公开过?用这个数据集进行时间序列模型预测是否有团队尝试过?
14、有个想法,对时序数据分类,可以看作一幅图,然后使用 CNN 去做图像分类吗?
下一篇:【动手学习深度学习】循环神经网络-2.文本预处理