蓝桥杯精选赛题算法系列——全球变暖——BFS

已收录此专栏。
我们先来举个例子来了解一下BFS的原理：
以老鼠走迷宫为例，迷宫内的路错综复杂，老鼠从入口进去后，怎么才能找到出口？
BFS：一群老鼠走迷宫。假设老鼠无限多，这群老鼠进去后，在每个路口，都派出部分老鼠探索所有没走过的路。走某条路的老鼠，如果碰壁无法前行，就停下；如果到达的路口已经有别的老鼠探索过了，也停下。很显然，在遇到出口前，所有的道路都会走到，而且不会重复。这个思路就是 BFS。
在具体编程时，一般用队列这种数据结构来实现 BFS ，即 “BFS = 队列”；而 DFS 一般用递归实现，即 “DFS = 递归”。
我们现在再进一步比较BFS和DFS来深度了解BFS：
前一讲学习了 DFS。
是不是觉得 DFS 是个死心眼啊。关于“一只老鼠走迷宫”的问题，DFS 的步骤是“一路走到底，直到碰壁；碰壁了回到上一步，换个路口继续一路走到底，直到碰壁…”。它完全不管当前这一步会不会走进一条死胡同，或者绕了远路。
比如下面的图，"@“是起点，”*“是终点，”#"是墙壁不能走，黑点是能走的下一步路口，只能上下左右走。

图1 一个迷宫图

那么要找从起点到终点的路，假设在每一步，都按先左再右的方法走，那么 DFS 结果就会是这样：

图1 DFS一条从"@“到”*"的路径

明明用两步能走到的路，却硬是走了13步。

不过会BFS的老鼠可没有这么笨拙偶。它就聪明多了，它在每个位置都“眼观八方”，把下一步可能走的路都试一遍，然后继续后面的路。那么它会怎么走呢？你看下图：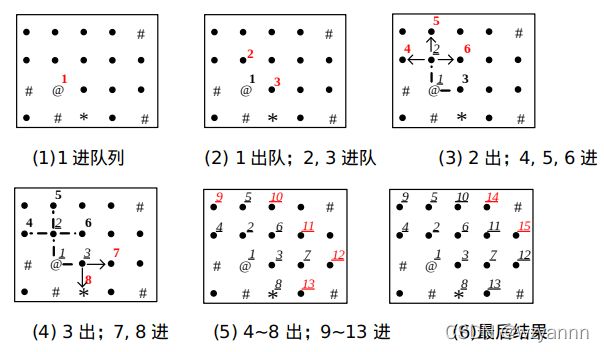
图3 BFS找从"@“到”*"的路径
所以这种聪明的老鼠的路线是：
1.从点 1 开始。
2.走到 1 的所有两个邻居 2、3。这时距离起点 1 一步远的两个点（2、3）都走到了。
3.继续走 2、3 的邻居。为了方便操作，让它按顺序来：先走 2 的所有邻居，（4、5、6） 就走到了。
4.然后再走 3 的邻居 7、8。这时距离起点 1 的两步远的点（4、5、6、7、8）都走到了。而且遇到了终点 8，只需两步！很聪明有没有！不过，这只老鼠为了显示自己的能干，决定继续把所有的点都走到。
5.走 4 的邻居 9、走 5 的邻居 10、走 6 的邻居 11，走 7 的邻居 12、13。这时距离起点 1 的三步远的点（9、10、11、12、13）都走到了。
6.再走，距离起点 11 的四步远的点（14、15）都走到了。
不仅仅如此，这只聪明的老鼠还发现，上面的步骤用队列来操作再简单不过了。我们帮它填个表详细说明如何用队列实现 BFS 的步骤吧。
接下来让我们来了解一下 BFS 的一些经典问题。

连通性问题

连通性判断是图论中的一个简单问题，就是找一张图中互相连通的部分，是基础的搜索，用 DFS 或 BFS 都行：
BFS判断连通性步骤：

1.从图上任意一个点 u 开始遍历，把它放进队列中。
2.弹出队首 u，标记 u 已经搜过，然后搜索 u 的邻居点，若邻居点符合连通条件，放到队列中。
3.继续弹出队首，标记搜过，然后搜索它的邻居，把符合连通条件的放进队列。继续以上步骤，直到队列为空。此时所有连通点都已经找到。

DFS判断连通性步骤是：

1.从图上任意一个点 u 开始遍历，标记 u 已经搜过。
2.递归 u 的所有符合连通条件的邻居点。
3.递归结束，找到所有连通点。

下面就让我们来道与连通性相关的蓝桥杯真题吧！

题目描述

你有一张某海域 NxN 像素的照片，".“表示海洋、”#"表示陆地，如下所示：

…

.##…

.##…

…##.

…####.

…###.

…

其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

…

…

…

…

…#…

…

…

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入描述

第一行包含一个整数 N (1≤N≤1000)。

以下 N 行 N 列代表一张海域照片。

照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

输出描述

输出一个整数表示答案。

样例输入

7
.......
.##....
.##....
....##.
..####.
...###.
.......

样例输出

1

解题思路：

显然这是一个连通性问题。步骤是：

1.遍历一个连通块（找到这个连通块中所有的’#‘，并标记已经搜过，不用再搜）；
2.再遍历下一个连通块…；
3.遍历完所有连通块，统计有多少个连通块。

def bfs(x,y):
    d = [(0,1),(0,-1),(1,0),(-1,0)]    
    q = [(x,y)]    #用list实现队列    
    vis[x][y]=1
    global flag    
    while q:            
        t=q.pop(0)          
        tx,ty = t[0],t[1]
        if mp[tx][ty+1]=='#' and mp[tx][ty-1]=='#' and \
           mp[tx+1][ty]=='#' and mp[tx-1][ty]=='#':
           flag = 1
        for i in range(4):
            nx = tx+d[i][0]
            ny = ty+d[i][1]
            if vis[nx][ny]==0 and mp[nx][ny]=="#":               
               q.append((nx,ny))                          
               vis[nx][ny]=1

n = int(input())
mp =[]
for i in range(n):
    mp.append(list(input()))
vis = []
for i in range(n):
    vis.append([0]*n)
ans = 0
for i in range(n):
    for j in range(n):
        if vis[i][j]==0 and mp[i][j]=="#":
            flag = 0
            bfs(i,j)
            if flag == 0:
                ans+=1
print(ans)

首先我们来解读一下，这个bfs的实现过程。
mp列表就是我们存储的陆地，海洋地图。vis列表是一个和mp列表同样规格的判断列表，用来帮助判断为“#”的陆地是否被判断过。减少程序的复杂度。
然后进入bfs函数，d列表是为之后用来搜索一个陆地“#”附近的‘#’，我们可以叫做它为方向列表。
而q列表是用来存储为判断过且搜索出来的”#”陆地的坐标。当q列表不包含任何参数的时候，我们就可以说，我们已经遍历一组陆地及其附近四周的陆地。

那么我们要思考一下，这个题的BFS的实现过程，是否和我们之前理解的BFS原理相同呢？
在这个题目中的实现过程主要是通过逐个遍历出来陆地，再对该陆地的上下左右四个方向进行遍历，依次不断向四周扩散，直至将所有陆地遍历完，该程序结束。
而我们之前所说的BFS的原理，不就是以队列的操作，向四周延伸至结束。
那么经过这个题我们要真正的学会BFS是怎么通过编程实现的，所以这块的编程思路我们需要多练习几遍：

def bfs(x,y):
    d = [(0,1),(0,-1),(1,0),(-1,0)]    
    q = [(x,y)]    #用list实现队列    
    vis[x][y]=1
    global flag    
    while q:            
        t=q.pop(0)          
        tx,ty = t[0],t[1]
        if mp[tx][ty+1]=='#' and mp[tx][ty-1]=='#' and \
           mp[tx+1][ty]=='#' and mp[tx-1][ty]=='#':
           flag = 1
        for i in range(4):
            nx = tx+d[i][0]
            ny = ty+d[i][1]
            if vis[nx][ny]==0 and mp[nx][ny]=="#":               
               q.append((nx,ny))                          
               vis[nx][ny]=1