【四】相机标定
- 【一】欧式空间、欧式变换
- 【二】[详细]针孔相机模型、相机镜头畸变模型、相机标定与OpenCV实现
- 【三】仿射变换、投影变换的矩阵形式和特点归纳
- 【四】相机标定
- 【五】边缘检测算子
- 【六】SVD分解
- 【七】GMS算法
- 【八】双边滤波
张氏标定法的原理
1.单应性矩阵H的计算
根据针孔相机模型,可以得到如下表达式:
s [ u v 1 ] = A [ R t ] [ X W Y W Z W 1 ] = A [ r 1 r 2 r 3 t ] [ X W Y W Z W 1 ] s\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=A\left[\begin{array}{ll} R & t \end{array}\right]\left[\begin{array}{c} X_{W} \\ Y_{W} \\ Z_{W} \\ 1 \end{array}\right]=A\left[\begin{array}{llll} r_{1} & r_{2} & r_{3} & t \end{array}\right]\left[\begin{array}{c} X_{W} \\ Y_{W} \\ Z_{W} \\ 1 \end{array}\right] s⎣⎡uv1⎦⎤=A[Rt]⎣⎢⎢⎡XWYWZW1⎦⎥⎥⎤=A[r1r2r3t]⎣⎢⎢⎡XWYWZW1⎦⎥⎥⎤
假设标定板所在的平面为世界坐标系所在的平面,即: Z w = 0 Z_{w}=0 Zw=0
则上式可以改写为:
s [ u v 1 ] = A [ R t ] [ X W Y W 0 1 ] = A [ r 1 r 2 t ] [ X W Y W 1 ] s\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=A\left[\begin{array}{ll} R & t \end{array}\right]\left[\begin{array}{c} X_{W} \\ Y_{W} \\ 0 \\ 1 \end{array}\right]=A\left[\begin{array}{lll} r_{1} & r_{2} & t \end{array}\right]\left[\begin{array}{c} X_{W} \\ Y_{W} \\ 1 \end{array}\right] s⎣⎡uv1⎦⎤=A[Rt]⎣⎢⎢⎡XWYW01⎦⎥⎥⎤=A[r1r2t]⎣⎡XWYW1⎦⎤
其中,矩阵H为:
H = A [ r 1 r 2 t ] = [ h 1 h 2 h 3 ] = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 1 ] H=A\left[\begin{array}{lll} r_{1} & r_{2} & t \end{array}\right]=\left[\begin{array}{lll} h_{1} & h_{2} & h_{3} \end{array}\right]=\left[\begin{array}{llc} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & 1 \end{array}\right] H=A[r1r2t]=[h1h2h3]=⎣⎡h11h21h31h12h22h32h13h231⎦⎤
则上式可以展开为:
{ s u = h 11 X + h 12 Y + h 13 s v = h 21 X + h 22 Y + h 23 s = h 31 X + h 32 Y + 1 \left\{\begin{array}{l} s u=h_{11} X+h_{12} Y+h_{13} \\ s v=h_{21} X+h_{22} Y+h_{23} \\ s=h_{31} X+h_{32} Y+1 \end{array}\right. ⎩⎨⎧su=h11X+h12Y+h13sv=h21X+h22Y+h23s=h31X+h32Y+1
将(3)中的s带入(1)(2)中得到:
{ ( h 31 X + h 32 Y + 1 ) u = h 11 X + h 12 Y + h 13 ( h 31 X + h 32 Y + 1 ) v = h 21 X + h 22 Y + h 23 \left\{\begin{array}{l} \left(h_{31} X+h_{32} Y+1\right) u=h_{11} X+h_{12} Y+h_{13} \\ \left(h_{31} X+h_{32} Y+1\right) v=h_{21} X+h_{22} Y+h_{23} \end{array}\right. {(h31X+h32Y+1)u=h11X+h12Y+h13(h31X+h32Y+1)v=h21X+h22Y+h23
令:
h ′ = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 ] h^{\prime}=\left[\begin{array}{llllllll} h_{11} & h_{12} & h_{13} & h_{21} & h_{22} & h_{23} & h_{31} & h_{32} \end{array}\right] h′=[h11h12h13h21h22h23h31h32]
则改写为矩阵形式为:
[ X Y 1 0 0 0 − u X − u Y − u 0 0 0 X Y 1 − v X − v Y − v ] h ′ = 0 \left[\begin{array}{lllllllll} X & Y & 1 & 0 & 0 & 0 & -u X & -u Y & -u \\ 0 & 0 & 0 & X & Y & 1 & -v X & -v Y & -v \end{array}\right] h^{\prime}=0 [X0Y0100X0Y01−uX−vX−uY−vY−u−v]h′=0
上式可以看作:
S h ′ = 0 S h^{\prime}=0 Sh′=0
那么矩阵 S T S S^{T}S STS最小特征值对应的特征向量就是该方程的最小二乘解,再将解归一化得到所需的 h ′ h^{\prime} h′,从而可以求得 H H H。但是由于线性解法所得到的解一般不是最优的解,所以可以选择上面两个等式中的一个,构建评价函数,利用LM算法计算出更高的精度解。
2.相机内外参求解
由于求得的H可能和真实的H相差一个比例因子,因此得到:
[ h 1 h 2 h 3 ] = λ A [ r 1 r 2 t ] \left[\begin{array}{lll} h_{1} & h_{2} & h_{3} \end{array}\right]=\lambda A\left[\begin{array}{lll} r_{1} & r_{2} & t \end{array}\right] [h1h2h3]=λA[r1r2t]
其中,内参A矩阵为:
A = [ a γ u 0 0 β v 0 0 0 1 ] A=\left[\begin{array}{ccc} a & \gamma & u_{0} \\ 0 & \beta & v_{0} \\ 0 & 0 & 1 \end{array}\right] A=⎣⎡a00γβ0u0v01⎦⎤
补充:三阶上三角、下三角矩阵求逆公式:
如果有可逆下三角矩阵:
A = [ m 0 0 a n 0 b c h ] A=\left[\begin{array}{lll} m & 0 & 0 \\ a & n & 0 \\ b & c & h \end{array}\right] A=⎣⎡mab0nc00h⎦⎤
则A的逆矩阵为:
A − 1 = [ 1 m 0 0 − a m n 1 n 0 a c − b n m n h − c n h 1 h ] A^{-1}=\left[\begin{array}{ccc} \frac{1}{m} & 0 & 0 \\ -\frac{a}{m n} &\frac{1}{n} & 0 \\ \frac{a c-b n}{m n h} & -\frac{c}{n h} & \frac{1}{h} \end{array}\right] A−1=⎣⎡m1−mnamnhac−bn0n1−nhc00h1⎦⎤
如果有可逆上三角矩阵:
B = [ m a b 0 n c 0 0 h ] B=\left[\begin{array}{lll} m & a & b \\ 0 & n & c \\ 0 & 0 & h \end{array}\right] B=⎣⎡m00an0bch⎦⎤
则B的逆矩阵为:
B − 1 = [ 1 m − a m n a c − b n m n h 0 n ˉ − c n h 0 0 1 h ] B^{-1}=\left[\begin{array}{ccc} \frac{1}{m} & -\frac{a}{m n} & \frac{a c-b n}{m n h} \\ 0 & \bar{n} & -\frac{c}{n h} \\ 0 & 0 & \frac{1}{h} \end{array}\right] B−1=⎣⎡m100−mnanˉ0mnhac−bn−nhch1⎦⎤
那么可以得到内参A矩阵的逆矩阵:
A − 1 = [ 1 a − γ a β γ v 0 − u 0 β a β 0 1 β − v 0 β 0 0 γ ] A^{-1}=\left[\begin{array}{ccc} \frac{1}{a} & -\frac{\gamma}{a \beta} & \frac{\gamma v_{0}-u_{0} \beta}{a \beta} \\ 0 & \frac{1}{\beta} & -\frac{v_{0}}{\beta} \\ 0 & 0 & \gamma \end{array}\right] A−1=⎣⎡a100−aβγβ10aβγv0−u0β−βv0γ⎦⎤
r 1 r_{1} r1和 r 2 r_{2} r2为单位正交向量,有 r 1 T r 1 = r 2 T r 2 = 1 r_{1}^{T} r_{1}=r_{2}^{T} r_{2}=1 r1Tr1=r2Tr2=1,所以上式可以得到两个约束条件:
{ h 1 T A − T A − 1 h 2 = 0 h 1 T A − T A − 1 h 1 = h 2 T A − T A − 1 h 2 \left\{\begin{array}{l} h_{1}^{T} A^{-T} A^{-1} h_{2}=0 \\ h_{1}^{T} A^{-T} A^{-1} h_{1}=h_{2}^{T} A^{-T} A^{-1} h_{2} \end{array}\right. {h1TA−TA−1h2=0h1TA−TA−1h1=h2TA−TA−1h2
令:
B = A − T A − 1 = [ B 11 B 12 B 13 B 21 B 22 B 23 B 31 B 32 B 33 ] = [ 1 a 2 − γ a 2 β v 0 γ − u 0 β a 2 β − γ a 2 β γ a 2 β 2 + 1 β 2 − γ ( v 0 γ − u 0 β ) a 2 β 2 − v 0 β 2 v 0 γ − u 0 β a 2 β − γ ( v 0 γ − u 0 β ) a 2 β 2 − v 0 β 2 − ( v 0 γ − u 0 β ) 2 a 2 β + v 0 2 β 2 + 1 ] \begin{array}{l} B=A^{-T} A^{-1}=\left[\begin{array}{lll} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{array}\right] =\\ \left[\begin{array}{ccc} \frac{1}{a^{2}} & -\frac{\gamma}{a^{2} \beta} & \frac{v_{0} \gamma-u_{0} \beta}{a^{2} \beta} \\ -\frac{\gamma}{a^{2} \beta} & \frac{\gamma}{a^{2} \beta^{2}}+\frac{1}{\beta^{2}} & -\frac{\gamma\left(v_{0} \gamma-u_{0} \beta\right)}{a^{2} \beta^{2}}-\frac{v_{0}}{\beta^{2}} \\ \frac{v_{0} \gamma-u_{0} \beta}{a^{2} \beta} & -\frac{\gamma\left(v_{0} \gamma-u_{0} \beta\right)}{a^{2} \beta^{2}}-\frac{v_{0}}{\beta^{2}} & -\frac{\left(v_{0} \gamma-u_{0} \beta\right)^{2}}{a^{2} \beta}+\frac{v_{0}^{2}}{\beta^{2}}+1 \end{array}\right] \end{array} B=A−TA−1=⎣⎡B11B21B31B12B22B32B13B23B33⎦⎤=⎣⎢⎡a21−a2βγa2βv0γ−u0β−a2βγa2β2γ+β21−a2β2γ(v0γ−u0β)−β2v0a2βv0γ−u0β−a2β2γ(v0γ−u0β)−β2v0−a2β(v0γ−u0β)2+β2v02+1⎦⎥⎤
从上可以看出B是一个对称矩阵,可以用6维向量定义:
b = [ B 11 B 12 B 22 B 13 B 23 B 33 ] ⊤ b=\left[\begin{array}{llllll} B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33} \end{array}\right]^{\top} b=[B11B12B22B13B23B33]⊤
假设H的第i列向量可以表示为
h i = [ h i 1 h i 2 h i 3 ] h_{i}=\left[\begin{array}{l} h_{i 1} \\ h_{i 2} \\ h_{i 3} \end{array}\right] hi=⎣⎡hi1hi2hi3⎦⎤
那么:
h i T B h i = V i j ⊤ b j h_{i}^{T} B h_{i}=V_{i j}^{\top} b_{j} hiTBhi=Vij⊤bj
其中:
V i j = [ h i 1 h j 1 h i 1 h j 2 + h i 2 h j 1 h i 2 h j 2 h i 3 h j 1 + h i 1 h j 3 h i 3 h j 2 + h i 2 h j 3 + h i 3 h j 3 ] ⊤ \begin{array}{l} V_{i j} =\left[\begin{array}{lllll} h_{i 1} h_{j 1} & h_{i 1} h_{j 2}+h_{i 2} h_{j 1} & h_{i 2} h_{j 2} & h_{i 3} h_{j 1}+h_{i 1} h_{j 3} & h_{i 3} h_{j 2}+h_{i 2} h_{j 3}+h_{i 3} h_{j 3} \end{array}\right]^{\top} \end{array} Vij=[hi1hj1hi1hj2+hi2hj1hi2hj2hi3hj1+hi1hj3hi3hj2+hi2hj3+hi3hj3]⊤
则可以得到:
[ V 12 T V 11 T − V 22 T ] b = 0 \left[\begin{array}{c} V_{12}^{T} \\ V_{11}^{T}-V_{22}^{T} \end{array}\right] b=0 [V12TV11T−V22T]b=0
其中,一个H构成两个约束,因此至少需要三个方程才可以求解出b,从而得到5个内参数:
{ v 0 = ( B 12 B 13 − B 11 B 23 ) / ( B 11 B 22 − B 12 2 ) λ = B 33 − [ B 13 2 + v 0 ( B 12 B 13 − B 11 B 23 ) ] / B 11 f u = λ / B 11 f v = λ B 11 / ( B 11 B 22 − B 12 2 ) s = − B 12 f u 2 f v / λ u 0 = s v 0 / f v − B 13 f u 2 / λ \left\{\begin{array}{l} v_{0}=\left(B_{12} B_{13}-B_{11} B_{23}\right) /\left(B_{11} B_{22}-B_{12}^{2}\right) \\ \lambda=B_{33}-\left[B_{13}^{2}+v_{0}\left(B_{12} B_{13}-B_{11} B_{23}\right)\right] / B_{11} \\ f_{u}=\sqrt{\lambda / B_{11}} \\ f_{v}=\sqrt{\lambda B_{11} /\left(B_{11} B_{22}-B_{12}^{2}\right)} \\ s=-B_{12} f_{u}^{2} f_{v} / \lambda \\ u_{0}=s v_{0} / f_{v}-B_{13} f_{u}^{2} / \lambda \end{array}\right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧v0=(B12B13−B11B23)/(B11B22−B122)λ=B33−[B132+v0(B12B13−B11B23)]/B11fu=λ/B11fv=λB11/(B11B22−B122)s=−B12fu2fv/λu0=sv0/fv−B13fu2/λ
再根据单应性矩阵H和内参矩阵A,利用如下公式,计算每幅图像的外参:
{ r 1 = λ A − 1 h 1 , r 2 = λ A − 1 h 2 , r 3 = r 1 × r 2 t = λ A − 1 h 3 , λ = 1 ∥ A − 1 h 1 ∥ = 1 ∥ A − 1 h 2 ∥ \left\{\begin{array}{l} r_{1}=\lambda A^{-1} h_{1}, r_{2}=\lambda A^{-1} h_{2}, r_{3}=r_{1} \times r_{2} \\ t=\lambda A^{-1} h_{3}, \lambda=\frac{1}{\left\|A^{-1} h_{1}\right\|}=\frac{1}{\left\|A^{-1} h_{2}\right\|} \end{array}\right. {r1=λA−1h1,r2=λA−1h2,r3=r1×r2t=λA−1h3,λ=∥A−1h1∥1=∥A−1h2∥1
由于图像中存在一些噪声,所以矩阵R事实上并不满足正交性质,所以根据最小距离准则取最佳的R解。
标定方法:
| 标定方法 | 优点 | 缺点 | 常见方法 |
|---|---|---|---|
| 标定物标定法 | 可使用任意的相机模型、精度高 | 需要标定物、算法复杂 | Tsai两步法、张氏标定法 |
| 相机自标定法 | 灵活性强、可在线标定 | 精度低、鲁棒性差 | 分层逐步标定、基于Kruppa方程 |
| 主动视觉相机标定法 | 不需要标定物、算法简单、鲁棒性高 | 成本高、设备昂贵、对于运动参数无法预知的情况不适用 | 主动系统控制相机做特定运动 |
| 标定方法 | 相机模型 | 畸变模型 | skewness | 原理 | 优点 | 缺点 |
|---|---|---|---|---|---|---|
| Tsai | 针孔相机模型 | 二阶 | 0 | 给定至少7组特征点的像素坐标和世界坐标,基于径向对齐构建超定线性方程组 | 精度高 | 需要精确的3D测量、耗时、采集数据易受噪声影响、大多数情况不宜使用 |
| zhang | 针孔相机模型 | 二阶+四阶 | 变量 | 计算每个棋盘格的单应性矩阵,至少3个视角的单应性矩阵已知,相机参数可以通过对这些矩阵的线性等式求解得到 | 需要的设备简单(标定板),可以实现较高的精度、灵活、适应性强 | 对噪声敏感,但是可以通过包含更多格子的棋盘格提高精度 |
- 注意:《Requirements for Camera Calibration: Must Accuracy Come with a High Price?》
- 零偏移假设,即s=0,一般情况下是合理的。
- 二阶足以模拟径向畸变模型,四阶在低噪声情况下可取,六阶将降低标定的性能。
- 添加切向畸变,一般可以提高标定的精度。
- 在拍摄时,标定板的图像应尽量覆盖整个视野的1/2左右,并且标定图片一般以20张为宜,实验证明,图片太多会导致参数优化的结果变差
标定板
精度:圆形标定板 > 角点标定板
圆形标定板
- halcon中圆形标定板

- 自制圆形标定板
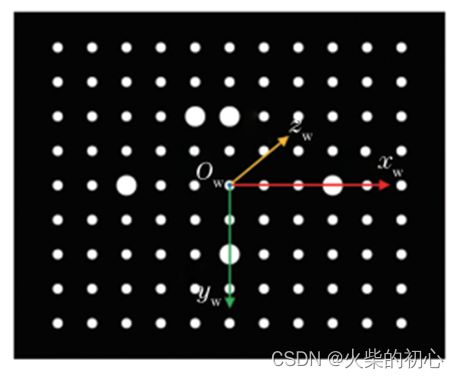
注意:在中间设置了不对称(既不是轴对称,也不是中心对称)的五个大圆,有两个目的: - 无论怎么摆设标定板,都不会改变圆的排序序号,即在相机标定时,在标定板上建立世界坐标系是唯一的,这在一定程度会提升相机标定的精度。
- 在标定时,由于相机视角原因,即使没有将标定板拍摄完全,也可以根据中间五个大圆,将图像上的圆正确排序。
角点标定板
可以满足VSLAM相机标定的需要

