使用基尼指数划分属性的决策树(CART)
本文是在之前基础上的修改,所以如果有问题可以看西瓜书中的决策树算法实现(ID3)这篇文章。
CART 决策树由[Breiman et al.] 在1984 年提出。其使用”基尼指数“用来划分属性。
基尼系数(英文:Gini index、Gini Coefficient)是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。
基尼系数最大为“1”,最小等于“0”。基尼系数越接近0表明收入分配越是趋向平等。国际惯例把0.2以下视为收入绝对平均,0.2-0.3视为收入比较平均;0.3-0.4视为收入相对合理;0.4-0.5视为收入差距较大,当基尼系数达到0.5以上时,则表示收入悬殊。
基尼指数最早由意大利统计与社会学家Corrado Gini在1912年提出。
【注】我看这个概念的时候完全忘记了自己在决策树,哈哈哈
根据这个概念不难看出,对于经济体来说,肯定是收入越平均越好,但是对于我们的系统来说,越平均系统的熵越高,系统越混乱。因此一个接近与1的系统,他的混乱都最低。
但是 ,并非如此。玛德,又一次理解错了,书中的概念是: 基尼指数越小越好,害,正好和理解的相反。然后我又找到了一篇文章。决策树:什么是基尼系数(“杂质 增益 指数 系数”辨析) 这个里面解释的很清楚,下面,我再去读一遍,国庆一个小假期忘得从差不多了…
基尼指数的原理就是,选择一个分类方式,原数据被分错的概率之和。借上文的图片一用:
 在上述分类器中,左侧共四个元素,全部正确分类 故
在上述分类器中,左侧共四个元素,全部正确分类 故
G l e f t = 4 4 ∗ ( 1 − 1 ) + 0 4 ∗ ( 1 − 0 ) = 0 G_{left}=\frac{4}{4}*(1-1)+\frac{0}{4}*(1-0)=0 Gleft=44∗(1−1)+40∗(1−0)=0
计算的公式是 (所占的比例*分错的概率)
下面计算右侧的概率:
G r i g h t = 5 6 ∗ ( 1 − 5 6 ) + 1 6 ∗ ( 1 − 1 6 ) = 10 36 = 0.278 G_{right}=\frac{5}{6}*(1-\frac{5}{6})+\frac{1}{6}*(1-\frac{1}{6})=\frac{10}{36}=0.278 Gright=65∗(1−65)+61∗(1−61)=3610=0.278
再计算下,未进行划分的时候,的基尼值
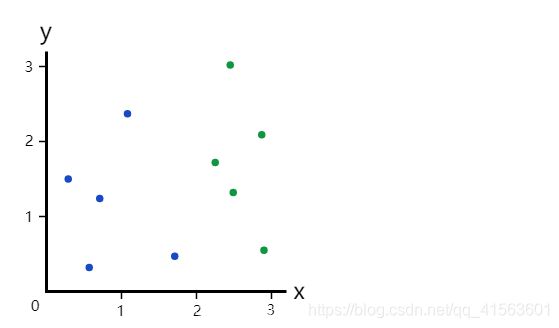 共10个点
共10个点
G = 5 10 ∗ ( 1 − 5 10 ) + 5 10 ∗ ( 1 − 5 10 ) = 1 2 = 0.5 G=\frac{5}{10}*(1-\frac{5}{10})+\frac{5}{10}*(1-\frac{5}{10})=\frac{1}{2}=0.5 G=105∗(1−105)+105∗(1−105)=21=0.5
也就是划分之后,基尼指数减小了,当两边都是完美划分的时候,基尼指数是0,这是我们想要的。现在知道怎么计算基尼指数了,也知道比较的标准了,下面开始改代码
首先还是使用第一版的代码进行修改:
原信息熵的计算代码为:
def Ent(D):
p=collect(D)
if (fabs(1.0 - p) < 0.000001) or (fabs(0.0 - p) < 0.000001):
return 0 #表示完全分割开了
return -p*np.log2(p)-(1-p)*np.log2(1-p)
下面修改为gini值的计算:
def Gini(D):
p=collect(D)+0.0000000000001 #同样的拿到当前数据集的正负标签比例
g=p*(1-p)+(1-p)*p
return g
原信息增益的函数为:
def Gain(D,a):
G=Ent(D)
index = static_attr.index(a)
lis=attr_dict[a]
temp_dict=split_data(D,a)
sum=0
for x in lis:
d=np.array(temp_dict[x])
sum+=(d.shape[0]/D.shape[0])*Ent(d)
return G-sum
现在修改为:
def Gini_index(D,a):
lis=attr_dict[a]
temp_dict=split_data(D,a)
sum=0
for x in lis:
d=np.array(temp_dict[x])
sum+=(d.shape[0]/D.shape[0])*Gini(d)
return sum
同时,原来选择最优属性,是根据信息增益最大的,原函数如下:
def select_opt_attr(D,d_attr):
li=[]
for x in d_attr:
li.append(Gain(D,x))
return d_attr[li.index(max(li))]
现在,应该是计算基尼指数最小的:做出如下修改:
def select_opt_attr(D,d_attr):
li=[]
for x in d_attr:
li.append(Gini_index(D,x))
return d_attr[li.index(min(li))]
至此,全部的修改都已完成。全部代码如下:注意数据集的位置
from math import fabs
import pandas as pd
import numpy as np
df=pd.read_csv("./ml2.0.csv")
# 属性集合
attr=df.columns.values.tolist()[1:]
data_org=np.array(df[attr[0:]])
static_attr=df.columns.values.tolist()[1:]#这里的属性 不改变,仅仅作为索引
attr_dict={}#用于记录每一个属性的取值
for x in attr:
temp=np.array(df[x])
attr_dict[x]=set(temp)
def label_is_same(D):
l=[D[i][-1] for i in range(len(D))]
return len(list(set(l)))==1
def all_attr_is_same(D,d_attr):
if D.shape[0]==0:return True #如果是空集
for x in d_attr:
index=static_attr.index(x)
for i in D[0:] :
if i[index]!=D[0][index]:
return False
return True
# 统计某个属性中,正样本和负样本的比例:
def collect(D):
if D.shape[0]==0:
return 0.0000000001
count= 0
for i in D:
count=count+1 if i[-1]=='是' else count
return count /(D.shape[0])
def Gini(D):
p=collect(D)+0.0000000000001 #同样的拿到当前数据集的正负标签比例
g=p*(1-p)+(1-p)*p
return g
def split_data(D,a):
index = static_attr.index(a)
lis=attr_dict[a]
temp_dict={}
for i in lis:
temp_dict[i]=[]
for i in D:
for at in lis:
if i[index]==at:
temp_dict[at].append(i)
break;
return temp_dict
def Gini_index(D,a):
lis=attr_dict[a]
temp_dict=split_data(D,a)
sum=0
for x in lis:
d=np.array(temp_dict[x])
sum+=(d.shape[0]/D.shape[0])*Gini(d)
return sum
def select_opt_attr(D,d_attr):
li=[]
for x in d_attr:
li.append(Gini_index(D,x))
return d_attr[li.index(min(li))]
node={}
def TreeGenerate(D,d_attr,node,father):#ID3算法
if D.shape[0]==0:
return
if label_is_same(D):
node['final']=D[-1][-1]
return
if len(d_attr)==0 or all_attr_is_same(D,d_attr):# 属性集为空 或者所有样本在说有属性上取值相同
node['final']='是' if collect(D)>0.5 else '否'
return
#选择最优的划分属性:
opt_attr=select_opt_attr(D,d_attr)
d_attr.remove(opt_attr)
#根据最优属性划分集合:
attr_dict=split_data(D,opt_attr)
node[opt_attr]={}
for i in attr_dict:
d1=np.array(attr_dict[i])
node[opt_attr][i]={}
TreeGenerate(d1,d_attr[:],node[opt_attr][i],i)
TreeGenerate(data_org,attr[:-1],node,"root")
print(node)
运行结果如下:
{'纹理': {
'模糊': {'final': '否'},
'清晰': {
'根蒂': {
'稍蜷': {
'色泽': {
'乌黑': {
'触感': {
'硬滑': {'final': '是'}, '软粘': {'final': '否'}}},
'青绿': {'final': '是'},
'浅白': {}}},
'硬挺': {'final': '否'},
'蜷缩': {'final': '是'}}},
'稍糊': {
'色泽': {
'乌黑': {
'敲声': {
'浊响': {'final': '是'},
'沉闷': {'final': '否'},
'清脆': {}}},
'青绿': {'final': '否'},
'浅白': {'final': '否'}}}}}
其实,还是有一点小问题的,感觉有部分是有冗余的,以后留给自己在修改吧,现在去看决策树的剪枝了。