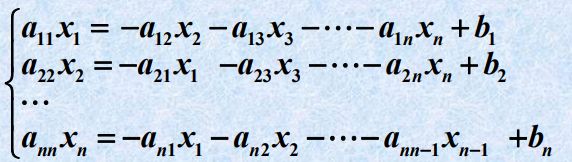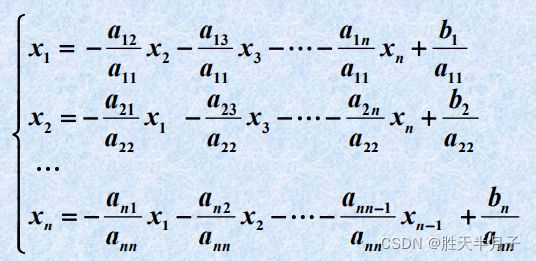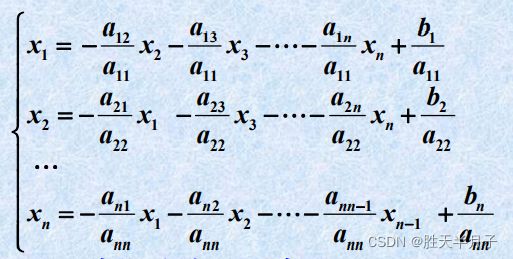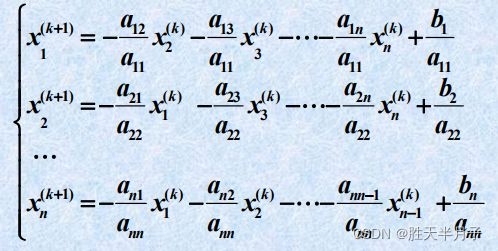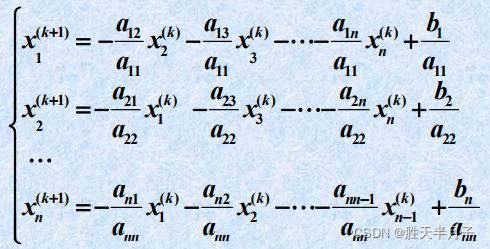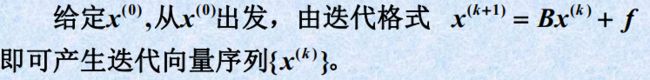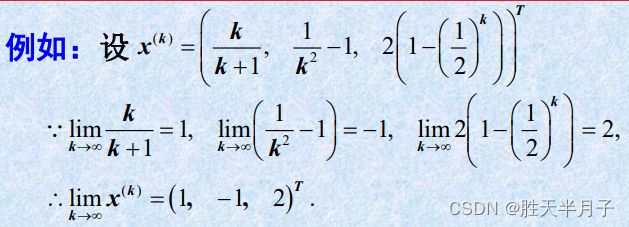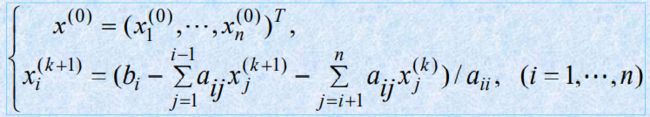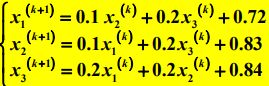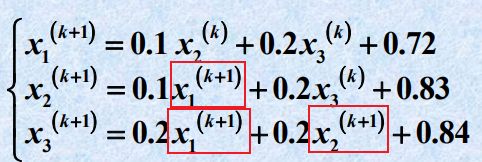- 龙芯架构适配:Qt 5.15.2 QWebEngine源码包推荐
曹勇宁
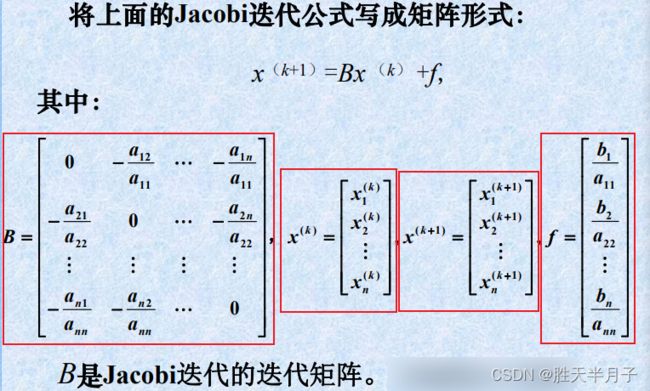
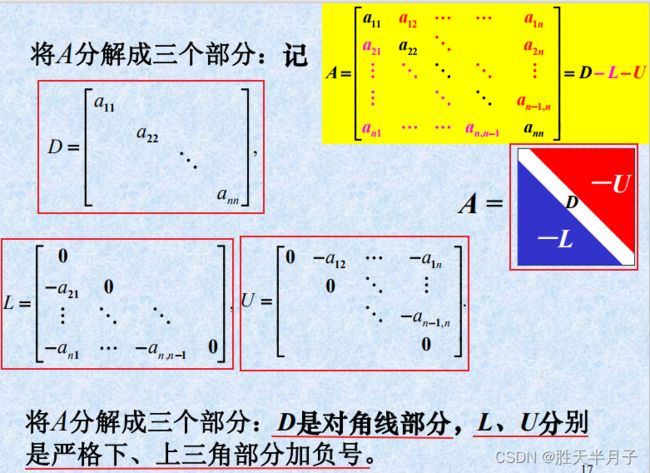
龙芯架构适配:Qt5.15.2QWebEngine源码包推荐【下载地址】Qt5.15.2QWebEngine适配龙芯LoongArch架构源码包本仓库提供了一个针对龙芯(LoongArch)架构的Qt5.15.2QWebEngine源码包,适用于UOS系统。由于标准的QWebEngine源码不支持LoongArch架构,因此需要进行适配才能在该架构的UOS系统上进行编译项目地址:https://g
- 使用 libevent 构建高性能网络应用
ScilogyHunter
常见软件库libevent事件驱动软件库
使用libevent构建高性能网络应用在现代网络编程中,高性能和可扩展性是开发者追求的核心目标。为了实现这一目标,许多开发者选择使用事件驱动库来管理I/O操作和事件处理。libevent是一个轻量级、高性能的事件通知库,广泛应用于网络服务器、代理、缓存等场景。本文将详细介绍libevent的核心概念、使用方法以及如何利用它构建高性能的网络应用。1.什么是libevent?libevent是一个用C
- 软件架构设计关键点:平衡高可用、性能、扩展性及成本的系统化实践
yinhezhanshen
程序人生系统架构
在数字化转型的浪潮中,软件系统已成为企业运营的核心支撑。从电商平台的秒杀活动到金融系统的实时交易,从物联网设备的百万级连接到政务服务的全天候响应,软件架构的设计质量直接决定了系统能否在复杂环境中稳定运行。本文将从高可用性、高性能、可扩展性、安全性、成本控制、规模承载和弹性伸缩七个维度,剖析现代软件架构设计的核心要点。一、高可用性:构建业务连续性的基石冗余设计:采用主从复制、多活数据中心架构(如
- 统一的视频动作模型
三谷秋水
计算机视觉机器学习人工智能计算机视觉深度学习机器学习人工智能
25年3月来自斯坦福大学的论文“UnifiedVideoActionModel”。统一的视频和动作模型对机器人技术具有重大意义,其中视频为动作预测提供丰富的场景信息,而动作为视频预测提供动态信息。然而,有效地结合视频生成和动作预测仍然具有挑战性,当前基于视频生成的方法在动作准确性和推理速度方面难以与直接策略学习的性能相匹配。为了弥补这一差距,引入统一的视频动作模型(UVA),它联合优化视频和动作预
- DeepSeek、Grok 与 ChatGPT 三巨头:技术架构与应用场景的全方位解析
云策量化
Deepseekchatgptdeepseekgrok
前言在当今人工智能领域,DeepSeek、Grok和ChatGPT作为语言模型的三巨头,各自凭借独特的技术架构和广泛的应用场景,在自然语言处理领域占据着重要地位。本文将对这三款模型的技术架构和应用场景进行全方位解析,以期为读者提供深入的了解和有价值的参考。一、技术架构(一)DeepSeekDeepSeek是由DeepSeek团队开发的一款大型语言模型,其技术架构基于深度学习中的Transforme
- Temu跨境新风口:2025年开店必知的账号安全指南
香菜9527
安全
近年来,Temu凭借其强大的供货链体系与超低价策略,成为跨境电商行业的新风口,吸引众多卖家入驻。随着平台竞争加剧,账号安全问题逐渐成为卖家面临的核心挑战。账号被封、资金冻结、违规操作等问题频发,轻则影响销量,重则导致店铺损失惨重。因此,了解并遵循安全运营规则,是每位卖家成功的关键。本文将为你详细解析Temu开店过程中必须掌握的账号安全知识,并提供实操建议,助你稳健运营。1.Temu账号安全为何重要
- 如何避免Bug跟踪系统混乱
管理前沿
运维人工智能大数据
流程规范化、工具集成化、沟通透明化。其中流程规范化通过明确每个环节的责任分工、标准化Bug报告和处理流程,有效减少混乱和重复劳动,确保Bug跟踪系统高效运转。企业通过数据分析发现,采用标准化流程后Bug处理效率可提升30%以上,这为软件质量控制提供了坚实保障。一、BUG跟踪系统的基本概念与重要性Bug跟踪系统是一种用于记录、管理和解决软件缺陷的工具和流程。它通过集中存储Bug报告、分类处理问题,并
- 侯捷 C++ 课程学习笔记:深入掌握 C++ 高阶特性 —— 实践与心得分享
清水白石008
C++学习笔记课程教程c++学习笔记
侯捷C++课程学习笔记:深入掌握C++高阶特性——实践与心得分享自从开始接触侯捷C++系列精品课程以来,我对C++语言有了全新的认识与深入理解。这套课程不仅系统地梳理了C++的基础知识,更从实际案例中展示了许多高阶特性和工程实战技巧。作为一名长期从事C++开发的专业人士,我深深感受到侯捷老师讲解中那种由浅入深、逻辑严密的魅力,也正是这种教学风格让我在短时间内掌握了不少难以琢磨的知识点。今天,我将结
- 探索AI模型的巅峰之战:ChatGPT、DeepSeek与Grok 3,谁才是最强?
温暖阳光阿斌
人工智能chatgpt
近年来,人工智能领域正处于一场高速迭代的革命中。大型语言模型(LLMs)如ChatGPT、DeepSeek和Grok3纷纷亮相,各展所长,为人们带来了前所未有的体验。在这场"谁是最强"的竞争中,每一方都展现出了令人惊叹的能力和独特的优势。然而,这些模型之间的差异和特点,究竟是什么?它们各自的优势在哪里?又有哪些隐藏的短板?本文将带您深入了解这三位AI巨头的亮点与争议,共同探讨它们在AI领域的位置,
- Python多进程Logging
ftpeak
Pythonpythonlinux开发语言logging
多个进程的logging向同一个.log文件写入是一套Python程序被多次启动时(多进程启动)无法回避的问题。一个进程的程序正在向.log文件写入的同时,另一个进行启动的程序也需要向同一个.log文件写入,会产生异常吗?答案是:会的!直接写入存在的问题如果多个进程直接使用Python的logging模块向同一个文件写入日志,可能会出现日志内容混乱、数据丢失等问题。这是因为多个进程同时访问和修改文
- OpenCV 4.2.0与扩展模块安装与应用指南
土城三富
本文还有配套的精品资源,点击获取简介:OpenCV4.2.0是一个先进的计算机视觉库,包含了图像处理、计算机视觉和机器学习算法。本压缩包包含OpenCV核心库和扩展模块(opencv_contrib),版本均为4.2.0。该版本引入了性能增强、API优化以及对深度学习框架和硬件加速技术的更新支持。扩展模块提供了额外的实验性算法和功能,有助于研究和开发新算法。指南详细介绍了如何安装和配置这些库,并提
- SQLAlchemy 的内存消耗
ftpeak
DBPython数据库pythonsql
为何要研究SQLAlchemy的内存消耗问题?因为SQLAlchemy在应用中,绝大多数问题体现在应用人员对SQLAlchemy的内存消耗问题不认知、不重视、不处理,最终造成整个系统的大问题,使SQLAlchemy的性能大打折扣,最终影响了SQLAlchemy的在您手中的可用性。通过以下解决问题的手法,可以有效控制SQLAlchemy的内存消耗,提高应用程序的性能和稳定性。1.连接池相关内存消耗原
- sql2019安装重启计算机失败,SQL SERVER 2019安装失败
小蛋子儿哦
Detailedresults:Feature:全文和语义提取搜索Status:失败Reasonforfailure:该功能的某个依赖项出错,导致该功能的安装过程失败。NextStep:使用以下信息解决错误,卸载此功能,然后再次运行安装过程。Componentname:SQLServer数据库引擎服务实例功能Componenterrorcode:0x80004005Errordescription
- Tenacity(Python的坚韧重试库)
ftpeak
Pythonpython开发语言网络爬虫
概述Tenacity是一个基于Apache2.0协议的通用重试库,用Python编写,旨在简化向任何代码添加重试逻辑的过程。它起源于已停止维护的retrying库的分叉版本。Tenacity不兼容retrying的API,但新增了大量功能并修复了长期存在的错误。文档:Tenacity—Tenacitydocumentation主页:https://github.com/jd/tenacity核心功
- matlab两矩阵相似性,两个矩阵同时相似对角化MATLAB程序.docx
weixin_39870664
matlab两矩阵相似性
两个矩阵同时相似对角化MATLAB程序摘要:使用Matlab语言设计出实现两个复矩阵同时相似对角化的计算机程序。关键词:同时相似对角化;Matlab;程序矩阵对角化是重要的数学方法,但因其计算过程繁琐,人们往往望之生畏,尤其是多个矩阵同时对角化问题,因此本文设计出判断及计算两个复矩阵能否同时相似对角化的Matlab程序,用此能够方便地解决两个复矩阵同时相似对角化问题。1.理论基础定义[1]:设A、
- C# 如何给kafka消息配置优先级按序消费
躺着发呆
C#大数据kafkac#分布式开发语言
顾名思义kafka消息主题是没有优先级的配置,没办法配置消费顺序的,所有我们需要想办法给kafka消息配置消费顺序,如何做呢?下面我给大家举个简单优先级事例,比如高中低三个顺序消费消息首先要定义三个消息主题,分别是高、中、低是哪个主题,英文分别是high、medium、low这个时候他们还是没有先后消费的本领,下面需要我们赋予他们这个顺序级别思路如下消费顺序,高》中》低,高和中都是可以插队来进行消
- java队列实现限流_如何使用队列实现微服务限流算法?
纽太普
java队列实现限流
队列在平时开发中可能是出现频率最高的数据结构之一了,但是大部分情况下,我们都是用别人已经实现好的,比如kafka,比如redis里的list,以至于让人怀疑为什么还要去学习队列呢?希望今天的内容可以给你一些启发。什么是队列为了整个文章的完整性,我们还是来介绍一下什么是队列。我们举个生活中常见的案例,假设你在周杰伦的奶茶店买奶茶,由于人很多,为了保持公平和秩序,你被要求排队,最先来的人排到最前面,这
- Pyhton安装PyQT6
三口一个桃
pythonpyqt
Windows系统使用CMD命令安装,对于系统中有多个版本python的,在安装pyqt6/pyqt5时需要针对每个python版本单独安装。安装准备过程:①Win+R打开CMD命令行窗口②输入命令:python--version查看当前python版本是否是自己需要安装pyqt6/5的的版本,若是则执行第③步,若不是则执行下述操作:打开电脑环境变量设置(自行百度)--点击系统变量中的Path项-
- 如何把master迁出的bug修改分支,合并、删除本地、删除远端
软考真题app
bug
要将fix/xxxxxx_20250319分支合并到master并删除本地及远程分支,请按以下步骤操作:1.切换到master分支并更新gitcheckoutmaster#切换到master分支gitpulloriginmaster#拉取远程master的最新代码2.合并分支到mastergitmergefix/xxxxxx_20250319#将fix/xxxxxx_20250319合并到当前分支
- Windows Docker Desktop 无法启动报错 Docker Desktop is shutting down 的可能解决办法
Bruce-li__
Dockerdocker容器运维
直接把整个AppData\Roaming\Docker目录删了,然后立刻就好了……这里还有一些其他的解决方案,Docker社区论坛也供参考:检查一下daemon.json配置文件是否有问题https://forums.docker.com/t/solved-docker-failed-to-start-docker-desktop-for-windows/106976
- YOLOV11|YOLO12改进系列指南
魔鬼面具
YOLO
基于Ultralytics的YOLO11|YOLO12改进目前自带的一些改进方案(持续更新)为了感谢各位对本项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程专栏改进汇总YOLO11系列二次创新系列ultralytics/cfg/models/11/yolo11-RevCol.yaml使用(ICLR2023)ReversibleColumnNetworks对yolo11主
- 记一次SQLServer2019安装和卸载问题的解决过程
JKRaks
数据库sqlserver
记一次SQLServer2019安装和卸载问题的解决过程Title.内容介绍0.起因1.卸载出现问题2.尝试直接安装尝试解决3.直接搞不了要不看看修复下头铁继续整注册表4.再次尝试安装累了,想重装了5.针对Couldnotopenkey找找找Answer.自己总结出来的解决步骤Title.内容介绍个人之前遇到的SQLServer因为卸载的时候出现的某些问题导致没有卸载完,然后在后来安装的时候的有些
- 使用ssh-keygen命令生成密钥对无密码远程登陆linux主机
哎哟喂我去
rhel6
我们在工作或试验中经常会需要登录多台linux主机进行操作,开启过多的ssh登陆界面,在不同的主机间切换时是非常让人的抓狂一件事情,只登陆一台linux主机然后通过此主机ssh登陆到其他主机这样是比较好的一种方式,但是在ssh登陆到其他主机时频繁的输入密码会让我们一直做重复的输入密码的工作,那有没有可以自动记住密码,或者不需要输入密码的工具呢?linux自带的ssh-kengen命令可以让我们轻松
- Android Compose 框架基本状态管理(mutableStateOf、State 接口)深入剖析(十四)
&有梦想的咸鱼&
android
AndroidCompose框架基本状态管理(mutableStateOf、State接口)深入剖析一、引言在Android开发的历史长河中,UI开发模式经历了从传统的XML布局到动态视图操作,再到如今声明式UI框架的转变。AndroidCompose作为Google推出的新一代声明式UI工具包,为开发者带来了全新的UI开发体验。其中,状态管理是Compose框架的核心概念之一,它决定了UI如何根
- PyQt6/PySide6 的 QSettings 类(配置管理)
燃灯工作室
Pysidepython开发语言
一、QSettings核心机制存储原理:基于键值对的持久化存储Windows:注册表路径HKEY_CURRENT_USER\Software\[组织名]\[应用名]macOS:~/Library/Preferences/[组织名].[应用名].plistLinux:~/.config/[组织名]/[应用名].conf基础代码框架:fromPySide6.QtCoreimportQSettings#
- Spring的JavaWeb三层架构
可问 可问春风
JAVASSM框架spring架构java
Spring三层架构的核心注解及协作在Spring的JavaWeb三层架构中,通过分层注解实现职责分离和组件管理,各层(表现层、业务层、数据访问层)的协作基于组件扫描和依赖注入(DI)机制。以下是各层的核心注解及其协作关系:1.分层架构与对应注解层级职责注解关联技术表现层处理用户请求,返回响应@Controller/@RestControllerSpringMVC,RESTfulAPI业务层实现业
- Linux find 命令完全指南
可问 可问春风
Linux从新手到入门linuxchrome运维
find是Linux系统最强大的文件搜索工具,支持嵌套遍历、条件筛选、执行动作。以下通过场景分类解析核心用法,涵盖高效搜索、文件管理及高级技巧:一、基础搜索模式1.按文件名搜索(精确/模糊匹配)find/path-name"*.log"#精确匹配.log后缀(区分大小写)find/home-iname"*.TXT"#模糊匹配.txt后缀(忽略大小写)find.-name"data_[0-9].cs
- 《代码拯救世界》
可问 可问春风
重生之我来csdn写小说网络计算机小说网络安全
《代码拯救世界》第一章:神秘的黑客组织“全球多个银行系统遭受黑客攻击,资金被大量转移,损失高达数十亿美元……”新闻播报员的声音在办公室里回荡,小陈的手心已经捏出了汗。作为一名网络安全工程师,他知道这次攻击的严重性远超普通黑客行为。“老李,你看这个。”小陈把一份报告递给同事,“攻击手法非常专业,利用了多个零日漏洞(未被公开的漏洞),而且目标明确,显然是早有预谋。”老李推了推眼镜,眉头紧锁:“这不像普
- Java面试宝典,kafka优先级队列
m0_57081324
程序员java经验分享面试
为什么要分库分表?首先回答一下为什么要分库分表,答案很简单:数据库出现性能瓶颈。用大白话来说就是数据库快扛不住了。数据库出现性能瓶颈,对外表现有几个方面:大量请求阻塞在高并发场景下,大量请求都需要操作数据库,导致连接数不够了,请求处于阻塞状态。SQL操作变慢如果数据库中存在一张上亿数据量的表,一条SQL没有命中索引会全表扫描,这个查询耗时会非常久。存储出现问题业务量剧增,单库数据量越来越大,给存储
- 一文说清预训练与微调:AI的双重训练法则
TGITCIC
AI-大模型的落地之道人工智能深度学习
什么是预训练?预训练是大型语言模型训练的第一步。它在资金和计算能力的支持下,通过深入分析大量的文本数据,使模型建立起语言的基本构架。在这一阶段,模型通过学习海量的书籍、文章和网页,识别出语言的语法、句法和词汇规律。这就如同一名学生接受通识教育,他并没有专注于某一门学科,而是获取了多方面的知识。自回归语言建模和掩码语言建模是预训练中常见的两种方法。前者在逐步构建文本的连贯性时,通过预测下一单词的方式
- jQuery 键盘事件keydown ,keypress ,keyup介绍
107x
jsjquerykeydownkeypresskeyup
本文章总结了下些关于jQuery 键盘事件keydown ,keypress ,keyup介绍,有需要了解的朋友可参考。
一、首先需要知道的是: 1、keydown() keydown事件会在键盘按下时触发. 2、keyup() 代码如下 复制代码
$('input').keyup(funciton(){
- AngularJS中的Promise
bijian1013
JavaScriptAngularJSPromise
一.Promise
Promise是一个接口,它用来处理的对象具有这样的特点:在未来某一时刻(主要是异步调用)会从服务端返回或者被填充属性。其核心是,promise是一个带有then()函数的对象。
为了展示它的优点,下面来看一个例子,其中需要获取用户当前的配置文件:
var cu
- c++ 用数组实现栈类
CrazyMizzz
数据结构C++
#include<iostream>
#include<cassert>
using namespace std;
template<class T, int SIZE = 50>
class Stack{
private:
T list[SIZE];//数组存放栈的元素
int top;//栈顶位置
public:
Stack(
- java和c语言的雷同
麦田的设计者
java递归scaner
软件启动时的初始化代码,加载用户信息2015年5月27号
从头学java二
1、语言的三种基本结构:顺序、选择、循环。废话不多说,需要指出一下几点:
a、return语句的功能除了作为函数返回值以外,还起到结束本函数的功能,return后的语句
不会再继续执行。
b、for循环相比于whi
- LINUX环境并发服务器的三种实现模型
被触发
linux
服务器设计技术有很多,按使用的协议来分有TCP服务器和UDP服务器。按处理方式来分有循环服务器和并发服务器。
1 循环服务器与并发服务器模型
在网络程序里面,一般来说都是许多客户对应一个服务器,为了处理客户的请求,对服务端的程序就提出了特殊的要求。
目前最常用的服务器模型有:
·循环服务器:服务器在同一时刻只能响应一个客户端的请求
·并发服务器:服
- Oracle数据库查询指令
肆无忌惮_
oracle数据库
20140920
单表查询
-- 查询************************************************************************************************************
-- 使用scott用户登录
-- 查看emp表
desc emp
- ext右下角浮动窗口
知了ing
JavaScriptext
第一种
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/
- 浅谈REDIS数据库的键值设计
矮蛋蛋
redis
http://www.cnblogs.com/aidandan/
原文地址:http://www.hoterran.info/redis_kv_design
丰富的数据结构使得redis的设计非常的有趣。不像关系型数据库那样,DEV和DBA需要深度沟通,review每行sql语句,也不像memcached那样,不需要DBA的参与。redis的DBA需要熟悉数据结构,并能了解使用场景。
- maven编译可执行jar包
alleni123
maven
http://stackoverflow.com/questions/574594/how-can-i-create-an-executable-jar-with-dependencies-using-maven
<build>
<plugins>
<plugin>
<artifactId>maven-asse
- 人力资源在现代企业中的作用
百合不是茶
HR 企业管理
//人力资源在在企业中的作用人力资源为什么会存在,人力资源究竟是干什么的 人力资源管理是对管理模式一次大的创新,人力资源兴起的原因有以下点: 工业时代的国际化竞争,现代市场的风险管控等等。所以人力资源 在现代经济竞争中的优势明显的存在,人力资源在集团类公司中存在着 明显的优势(鸿海集团),有一次笔者亲自去体验过红海集团的招聘,只 知道人力资源是管理企业招聘的 当时我被招聘上了,当时给我们培训 的人
- Linux自启动设置详解
bijian1013
linux
linux有自己一套完整的启动体系,抓住了linux启动的脉络,linux的启动过程将不再神秘。
阅读之前建议先看一下附图。
本文中假设inittab中设置的init tree为:
/etc/rc.d/rc0.d
/etc/rc.d/rc1.d
/etc/rc.d/rc2.d
/etc/rc.d/rc3.d
/etc/rc.d/rc4.d
/etc/rc.d/rc5.d
/etc
- Spring Aop Schema实现
bijian1013
javaspringAOP
本例使用的是Spring2.5
1.Aop配置文件spring-aop.xml
<?xml version="1.0" encoding="UTF-8"?>
<beans
xmlns="http://www.springframework.org/schema/beans"
xmln
- 【Gson七】Gson预定义类型适配器
bit1129
gson
Gson提供了丰富的预定义类型适配器,在对象和JSON串之间进行序列化和反序列化时,指定对象和字符串之间的转换方式,
DateTypeAdapter
public final class DateTypeAdapter extends TypeAdapter<Date> {
public static final TypeAdapterFacto
- 【Spark八十八】Spark Streaming累加器操作(updateStateByKey)
bit1129
update
在实时计算的实际应用中,有时除了需要关心一个时间间隔内的数据,有时还可能会对整个实时计算的所有时间间隔内产生的相关数据进行统计。
比如: 对Nginx的access.log实时监控请求404时,有时除了需要统计某个时间间隔内出现的次数,有时还需要统计一整天出现了多少次404,也就是说404监控横跨多个时间间隔。
Spark Streaming的解决方案是累加器,工作原理是,定义
- linux系统下通过shell脚本快速找到哪个进程在写文件
ronin47
一个文件正在被进程写 我想查看这个进程 文件一直在增大 找不到谁在写 使用lsof也没找到
这个问题挺有普遍性的,解决方法应该很多,这里我给大家提个比较直观的方法。
linux下每个文件都会在某个块设备上存放,当然也都有相应的inode, 那么透过vfs.write我们就可以知道谁在不停的写入特定的设备上的inode。
幸运的是systemtap的安装包里带了inodewatch.stp,位
- java-两种方法求第一个最长的可重复子串
bylijinnan
java算法
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
public class MaxPrefix {
public static void main(String[] args) {
String str="abbdabcdabcx";
- Netty源码学习-ServerBootstrap启动及事件处理过程
bylijinnan
javanetty
Netty是采用了Reactor模式的多线程版本,建议先看下面这篇文章了解一下Reactor模式:
http://bylijinnan.iteye.com/blog/1992325
Netty的启动及事件处理的流程,基本上是按照上面这篇文章来走的
文章里面提到的操作,每一步都能在Netty里面找到对应的代码
其中Reactor里面的Acceptor就对应Netty的ServerBo
- servelt filter listener 的生命周期
cngolon
filterlistenerservelt生命周期
1. servlet 当第一次请求一个servlet资源时,servlet容器创建这个servlet实例,并调用他的 init(ServletConfig config)做一些初始化的工作,然后调用它的service方法处理请求。当第二次请求这个servlet资源时,servlet容器就不在创建实例,而是直接调用它的service方法处理请求,也就是说
- jmpopups获取input元素值
ctrain
JavaScript
jmpopups 获取弹出层form表单
首先,我有一个div,里面包含了一个表单,默认是隐藏的,使用jmpopups时,会弹出这个隐藏的div,其实jmpopups是将我们的代码生成一份拷贝。
当我直接获取这个form表单中的文本框时,使用方法:$('#form input[name=test1]').val();这样是获取不到的。
我们必须到jmpopups生成的代码中去查找这个值,$(
- vi查找替换命令详解
daizj
linux正则表达式替换查找vim
一、查找
查找命令
/pattern<Enter> :向下查找pattern匹配字符串
?pattern<Enter>:向上查找pattern匹配字符串
使用了查找命令之后,使用如下两个键快速查找:
n:按照同一方向继续查找
N:按照反方向查找
字符串匹配
pattern是需要匹配的字符串,例如:
1: /abc<En
- 对网站中的js,css文件进行打包
dcj3sjt126com
PHP打包
一,为什么要用smarty进行打包
apache中也有给js,css这样的静态文件进行打包压缩的模块,但是本文所说的不是以这种方式进行的打包,而是和smarty结合的方式来把网站中的js,css文件进行打包。
为什么要进行打包呢,主要目的是为了合理的管理自己的代码 。现在有好多网站,你查看一下网站的源码的话,你会发现网站的头部有大量的JS文件和CSS文件,网站的尾部也有可能有大量的J
- php Yii: 出现undefined offset 或者 undefined index解决方案
dcj3sjt126com
undefined
在开发Yii 时,在程序中定义了如下方式:
if($this->menuoption[2] === 'test'),那么在运行程序时会报:undefined offset:2,这样的错误主要是由于php.ini 里的错误等级太高了,在windows下错误等级
- linux 文件格式(1) sed工具
eksliang
linuxlinux sed工具sed工具linux sed详解
转载请出自出处:
http://eksliang.iteye.com/blog/2106082
简介
sed 是一种在线编辑器,它一次处理一行内容。处理时,把当前处理的行存储在临时缓冲区中,称为“模式空间”(pattern space),接着用sed命令处理缓冲区中的内容,处理完成后,把缓冲区的内容送往屏幕。接着处理下一行,这样不断重复,直到文件末尾
- Android应用程序获取系统权限
gqdy365
android
引用
如何使Android应用程序获取系统权限
第一个方法简单点,不过需要在Android系统源码的环境下用make来编译:
1. 在应用程序的AndroidManifest.xml中的manifest节点
- HoverTree开发日志之验证码
hvt
.netC#asp.nethovertreewebform
HoverTree是一个ASP.NET的开源CMS,目前包含文章系统,图库和留言板功能。代码完全开放,文章内容页生成了静态的HTM页面,留言板提供留言审核功能,文章可以发布HTML源代码,图片上传同时生成高品质缩略图。推出之后得到许多网友的支持,再此表示感谢!留言板不断收到许多有益留言,但同时也有不少广告,因此决定在提交留言页面增加验证码功能。ASP.NET验证码在网上找,如果不是很多,就是特别多
- JSON API:用 JSON 构建 API 的标准指南中文版
justjavac
json
译文地址:https://github.com/justjavac/json-api-zh_CN
如果你和你的团队曾经争论过使用什么方式构建合理 JSON 响应格式, 那么 JSON API 就是你的 anti-bikeshedding 武器。
通过遵循共同的约定,可以提高开发效率,利用更普遍的工具,可以是你更加专注于开发重点:你的程序。
基于 JSON API 的客户端还能够充分利用缓存,
- 数据结构随记_2
lx.asymmetric
数据结构笔记
第三章 栈与队列
一.简答题
1. 在一个循环队列中,队首指针指向队首元素的 前一个 位置。
2.在具有n个单元的循环队列中,队满时共有 n-1 个元素。
3. 向栈中压入元素的操作是先 移动栈顶指针&n
- Linux下的监控工具dstat
网络接口
linux
1) 工具说明dstat是一个用来替换 vmstat,iostat netstat,nfsstat和ifstat这些命令的工具, 是一个全能系统信息统计工具. 与sysstat相比, dstat拥有一个彩色的界面, 在手动观察性能状况时, 数据比较显眼容易观察; 而且dstat支持即时刷新, 譬如输入dstat 3, 即每三秒收集一次, 但最新的数据都会每秒刷新显示. 和sysstat相同的是,
- C 语言初级入门--二维数组和指针
1140566087
二维数组c/c++指针
/*
二维数组的定义和二维数组元素的引用
二维数组的定义:
当数组中的每个元素带有两个下标时,称这样的数组为二维数组;
(逻辑上把数组看成一个具有行和列的表格或一个矩阵);
语法:
类型名 数组名[常量表达式1][常量表达式2]
二维数组的引用:
引用二维数组元素时必须带有两个下标,引用形式如下:
例如:
int a[3][4]; 引用:
- 10点睛Spring4.1-Application Event
wiselyman
application
10.1 Application Event
Spring使用Application Event给bean之间的消息通讯提供了手段
应按照如下部分实现bean之间的消息通讯
继承ApplicationEvent类实现自己的事件
实现继承ApplicationListener接口实现监听事件
使用ApplicationContext发布消息