Vision Transformer（ViT）PyTorch代码全解析（附图解）

Vision Transformer（ViT）PyTorch代码全解析

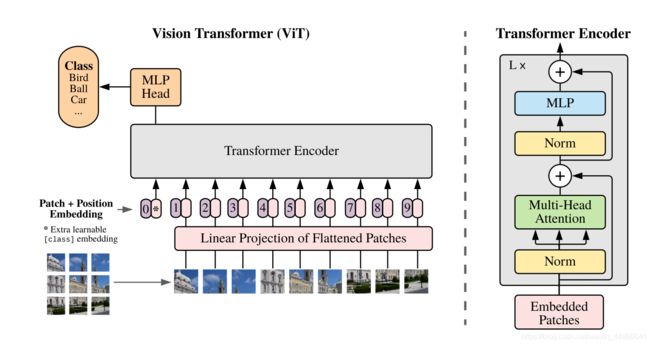
最近CV领域的Vision Transformer将在NLP领域的Transormer结果借鉴过来，屠杀了各大CV榜单。本文将根据最原始的Vision Transformer论文，及其PyTorch实现，将整个ViT的代码做一个全面的解析。

对原Transformer还不熟悉的读者可以看一下Attention is All You Need原文，中文讲解推荐李宏毅老师的视频 YouTube，BiliBili 个人觉得讲的很明白。

话不多说，直接开始。

下图是ViT的整体框架图，我们在解析代码时会参照此图：

以下是文中给出的符号公式，也是我们解析的重要参照：
$$\mathbf{z}=[{\mathbf{x}}_{class};{\mathbf{x}}_p^1\mathbf{E},{\mathbf{x}}_p^2\mathbf{E},\dots ;{\mathbf{x}}_p^N\mathbf{E}]+{\mathbf{E}}_{pos},\mathbf{E}\in {\mathbb{R}}^{(P^2\cdot C)\times D},{\mathbf{E}}_{pos}\in {\mathbb{R}}^{(N+1)\times D}(1)$$

$${\mathbf{z}}_{\mathbf{\ell }}^{\prime }=MSA(LN({\mathbf{z}}_{\ell -1}))+{\mathbf{z}}_{\ell -1}(2)$$

$${\mathbf{z}}_{\ell }=MLP(LN({{\mathbf{z}}^{\prime }}_{\ell }))+{{\mathbf{z}}^{\prime }}_{\ell }(3)$$

$$\mathbf{y}=LN({\mathbf{z}}_L^0)(4)$$

导入需要的包

import torch
from torch import nn, einsum
import torch.nn.functional as F

from einops import rearrange, repeat
from einops.layers.torch import Rearrange

都是搭建网络时常用的PyTorch包，其中在卷积神经网络的搭建中并不常用的einops和einsum，还不熟悉的读者可以参考博客：einops和einsum：直接操作张量的利器。

pair函数

def pair(t):
    return t if isinstance(t, tuple) else (t, t)

作用是：判断t是否是元组，如果是，直接返回t；如果不是，则将t复制为元组(t, t)再返回。
用来处理当给出的图像尺寸或块尺寸是int类型（如224）时，直接返回为同值元组（如(224, 224)）。

PreNorm

class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)

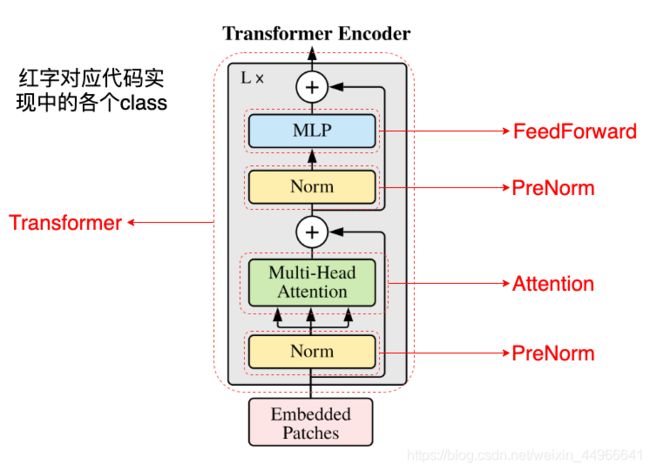
PreNorn对应框图中最下面的黄色的Norm层。其参数dim是维度，而fn则是预先要进行的处理函数，是以下的Attention、FeedForward之一，分别对应公式（2）（3）。
$${\mathbf{z}}_{\mathbf{\ell }}^{\prime }=MSA(LN({\mathbf{z}}_{\ell -1}))+{\mathbf{z}}_{\ell -1}(2)$$

$${\mathbf{z}}_{\ell }=MLP(LN({{\mathbf{z}}^{\prime }}_{\ell }))+{{\mathbf{z}}^{\prime }}_{\ell }(3)$$

FeedForward

class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout=0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim), 
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)

FeedForward层由全连接层，配合激活函数GELU和Dropout实现，对应框图中蓝色的MLP。参数dim和hidden_dim分别是输入输出的维度和中间层的维度，dropour则是dropout操作的概率参数p。

Attention

   
class Attention(nn.Module):              
    def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
        super().__init__()
        inner_dim = dim_head * heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim=-1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout),
        ) if project_out else nn.Identity()

    def forward(self, x):
        b, n, _, h = *x.shape, self.heads
        qkv = self.to_qkv(x).chunk(3, dim=-1)           # (b, n(65), dim*3) ---> 3 * (b, n, dim)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)          # q, k, v   (b, h, n, dim_head(64))

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale

        attn = self.attend(dots)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

Attention，Transformer中的核心部件，对应框图中的绿色的Multi-Head Attention。参数heads是多头自注意力的头的数目，dim_head是每个头的维度。

本层的对应公式就是经典的Tansformer的计算公式：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

Transformer

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout))
            ]))
    
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

定义好几个层之后，我们就可以构建整个Transformer Block了，即对应框图中的整个右半部分Transformer Encoder。有了前面的铺垫，整个Block的实现看起来非常简洁。

参数depth是每个Transformer Block重复的次数，其他参数与上面各个层的介绍相同。

笔者也在图中也做了标注与代码的各部分对应。

ViT

class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=3, dim_head=64, dropout=0., emb_dropout=0.):
        super().__init__()
        image_height, image_width = pair(image_size)
        patch_height, patch_width = pair(patch_size)

        assert  image_height % patch_height ==0 and image_width % patch_width == 0

        num_patches = (image_height // patch_height) * (image_width // patch_width)
        patch_dim = channels * patch_height * patch_width
        assert pool in {'cls', 'mean'}

        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width),
            nn.Linear(patch_dim, dim)
        )

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))					# nn.Parameter()定义可学习参数
        self.dropout = nn.Dropout(emb_dropout)

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )

    def forward(self, img):
        x = self.to_patch_embedding(img)        # b c (h p1) (w p2) -> b (h w) (p1 p2 c) -> b (h w) dim
        b, n, _ = x.shape           # b表示batchSize, n表示每个块的空间分辨率, _表示一个块内有多少个值

        cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)  # self.cls_token: (1, 1, dim) -> cls_tokens: (batchSize, 1, dim)  
        x = torch.cat((cls_tokens, x), dim=1)               # 将cls_token拼接到patch token中去       (b, 65, dim)
        x += self.pos_embedding[:, :(n+1)]                  # 加位置嵌入（直接加）      (b, 65, dim)
        x = self.dropout(x)

        x = self.transformer(x)                                                 # (b, 65, dim)

        x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]                   # (b, dim)

        x = self.to_latent(x)                                                   # Identity (b, dim)
        print(x.shape)

        return self.mlp_head(x)                                                 #  (b, num_classes)

笔者在forward()函数代码中的注释说明了各中间state的尺寸形状，可供参考比对。

在 x 送入transformer之前，都是对应公式（1）的预处理操作：
$$\mathbf{z}=[{\mathbf{x}}_{class};{\mathbf{x}}_p^1\mathbf{E},{\mathbf{x}}_p^2\mathbf{E},\dots ;{\mathbf{x}}_p^N\mathbf{E}]+{\mathbf{E}}_{pos},\mathbf{E}\in {\mathbb{R}}^{(P^2\cdot C)\times D},{\mathbf{E}}_{pos}\in {\mathbb{R}}^{(N+1)\times D}(1)$$
positional embedding和class token由nn.Parameter()定义，该函数会将送到其中的Tensor注册到Parameters列表，随模型一起训练更新，对nn.Parameter()不熟悉的同学可参考博客：PyTorch中的torch.nn.Parameter() 详解。

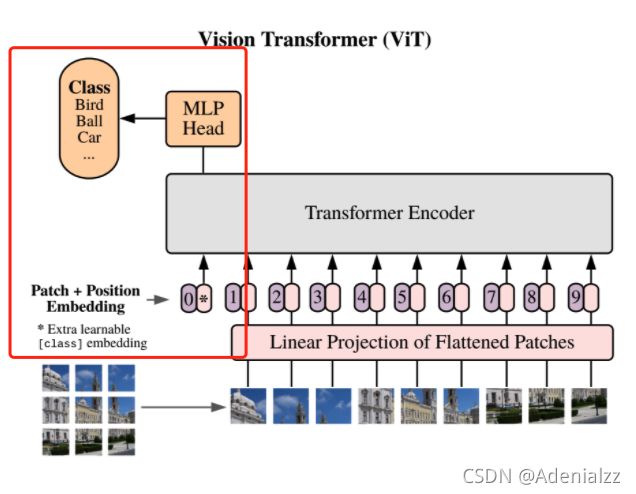
我们知道，transformer模型最后送到mlp中做预测的只有cls_token的输出结果（如上图红框所示），而其他的图像块的输出全都不要了，是由这一步实现：

x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]                   # (b, dim)

可以看到，如果指定池化方式为'mean'的话，则会对全部token做平均池化，然后全部进行送到mlp中，但是我们可以看到，默认的self.pool='cls'，也就是说默认不会进行平均池化，而是按照ViT的设计只使用cls_token，即x[:, 0]只取第一个token（cls_token）。

最后经过mlp_head，得到各类的预测值。

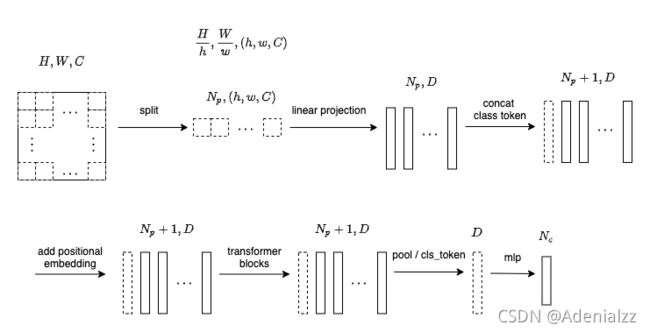
笔者也简单做了一张图展示整个过程中的信号流，可以结合代码中注释的维度的变化来看：

图中各符号含义：$H,W,C$ 分别是某一张输入图像的长、宽、通道数，$h,w$ 是图块的长、宽，如此这张图中块的个数就是 $\frac{H}{h}\times \frac{W}{w}$ ，用 $N_p$ 表示，$D$ 是维度数dim，$N_c$ 是类的个数。

至此，ViT模型的定义就全部完成了，在训练脚本中实例化一个ViT模型来进行训练即可，以下脚本可验证ViT模型正常运作。

model_vit = ViT(
        image_size = 256,
        patch_size = 32,
        num_classes = 1000,
        dim = 1024,
        depth = 6,
        heads = 16,
        mlp_dim = 2048,
        dropout = 0.1,
        emb_dropout = 0.1
    )

img = torch.randn(16, 3, 256, 256)

preds = model_vit(img) 

print(preds.shape)  # (16, 1000)

有疑惑或异议欢迎留言讨论。