统计学习方法(6)梯度提升决策树GBDT
统计学习方法(6)梯度提升决策树GBDT
梯度提升决策树 GBDT
- GBDT 是以
决策树为基学习器、采用Boosting策略的一种集成学习模型; - 与提升树的区别:残差的计算不同,
提升树使用的是真正的残差,梯度提升树用当前模型的负梯度来拟合残差。
1、提升树 Boosting Tree
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同:
- 用
平方误差损失函数的回归问题; - 用
指数损失函数的分类问题; - 用
一般损失函数的一般决策问题。
对于二类分类问题,提升树算法只需将AdaBoost算法中的基本分类器限制为二类分类树即可,可以说这时的提升树算法是AdaBoost算法的特殊情况,算法过程同AdaBoost算法一样。
下面主要介绍回归问题的提升树:
- 解决回归问题时,通过不断拟合残差得到新的树。
- 提升树模型可表示为决策树的加法模型:
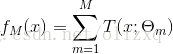
- 首先初始化提升树 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0,则第 m 步的模型为:
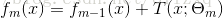
其中, T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)是第m步进行最优划分时产生的模型。 - 然后通过最小化损失函数决定下一个决策树的参数:
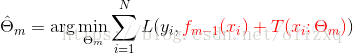
当采用平方误差损失函数时:
L ( y , f ( x ) ) = ( y − f ( x ) ) 2 L(y,f(x)) = (y-f(x))^2 L(y,f(x))=(y−f(x))2
其损失变为:
L ( y , f m − 1 ( x ) + T ( x ; Θ m ) ) = [ y − f m − 1 ( x ) − T ( x ; Θ m ) ] 2 = [ r − T ( x ; Θ m ] 2 \left. \begin{array}{l} \text{$\quad L(y,f_{m-1}(x)+T(x;\Theta_m))$}\\ \text{$=[y-f_{m-1}(x)-T(x;\Theta_m)]^2$}\\ \text{$=[r-T(x;\Theta_m]^2$} \end{array} \right. L(y,fm−1(x)+T(x;Θm))=[y−fm−1(x)−T(x;Θm)]2=[r−T(x;Θm]2
其中, r = y − f m − 1 ( x ) r = y-f_{m-1}(x) r=y−fm−1(x)是当前模型拟合数据的残差,所以,对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
提升树算法描述
在回归问题中,新的树是通过不断拟合残差(residual)得到的。
输入:训练集 T = ( x 1 , y 1 ) , . . , ( x N , y N ) , x i ∈ R n , y i ∈ R T={(x_1,y_1),..,(x_N,y_N)}, x_i ∈ R^n, y_i \in R T=(x1,y1),..,(xN,yN),xi∈Rn,yi∈R
输出:回归提升树 f M ( x ) f_M(x) fM(x)
(1)初始化 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0
(2)对 m = 1 , 2 , . . , M m=1,2,..,M m=1,2,..,M
(a)计算残差:
![]()
(b)拟合残差学习下一个回归树 T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)的参数:
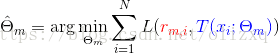
(c)更新 f m ( x ) f_m(x) fm(x):
![]()
(3)得到回归提升树:
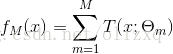
2、梯度提升(GB)算法
- 当损失函数为平方损失或指数损失时,每一步的优化是很直观的;但对于一般的损失函数而言,不太容易——梯度提升正是针对这一问题提出的算法;
- 梯度提升是梯度下降的近似方法,其关键是
利用损失函数的负梯度作为残差的近似值,来拟合下一个决策树。
2.1 GBDT 回归算法
2.2 GBDT 分类算法
以上是关于GBDT实现回归的算法过程,下面来看看GBDT分类算法,GBDT的分类算法从思想上和GBDT的回归算法没有区别,但是由于样本输出不是连续的值,而是离散的类别,导致我们无法直接从输出类别去拟合类别输出的误差。
为了解决这个问题,主要有两个方法:
- 一个是用指数损失函数,此时GBDT退化为Adaboost算法;
- 另一种方法是用类似于逻辑回归的对数似然损失函数的方法。
也就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。下面仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数,又有二元分类和多元分类的区别。
二元GBDT分类算法:
对于二元GBDT,如果用类似于逻辑回归的对数似然损失函数:
P ( y = 1 ∣ x ) = 1 1 + e − f ( x ) P(y=1|x) = {1 \over 1 + e^{- f(x)}} P(y=1∣x)=1+e−f(x)1 P ( y = − 1 ∣ x ) = e − f ( x ) 1 + e − f ( x ) P(y=-1|x) = {e^{- f(x)} \over 1 + e^{- f(x)}} P(y=−1∣x)=1+e−f(x)e−f(x)其中:当 y y y与 f ( x ) f(x) f(x)相同时概率较大,不同时概率较小。
写成一个表达式,得到:
P ( Y ∣ x ) = 1 1 + e − y f ( x ) P(Y|x) = {1 \over 1 + e^{- yf(x)}} P(Y∣x)=1+e−yf(x)1
则损失函数为:
L ( Y , f ( x ) ) = − l o g P ( Y ∣ x ) = l o g ( 1 + e x p ( − y f ( x ) ) ) L(Y,f(x)) = -log P(Y \mid x) = log(1+exp(-yf(x))) L(Y,f(x))=−logP(Y∣x)=log(1+exp(−yf(x)))
其中 y ∈ { − 1 , + 1 } y∈\{−1,+1\} y∈{−1,+1}。则此时的负梯度误差为:
r t i = − [ ∂ L ( y , f ( x i ) ) ) ∂ f ( x i ) ] f ( x ) = f t − 1 ( x ) = y i / ( 1 + e x p ( y i f ( x i ) ) ) r_{ti} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} = y_i/(1+exp(y_if(x_i))) rti=−[∂f(xi)∂L(y,f(xi)))]f(x)=ft−1(x)=yi/(1+exp(yif(xi)))
对于生成的决策树,我们各个叶子节点的最佳残差拟合值为:
c t j = a r g m i n ⎵ c ∑ x i ∈ R t j l o g ( 1 + e x p ( − y i ( f t − 1 ( x i ) + c ) ) ) c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} log(1+exp(-y_i(f_{t-1}(x_i) +c))) ctj=c argminxi∈Rtj∑log(1+exp(−yi(ft−1(xi)+c)))
由于上式比较难优化,我们一般使用近似值代替:
c t j = ∑ x i ∈ R t j r t i / ∑ x i ∈ R t j ∣ r t i ∣ ( 1 − ∣ r t i ∣ ) c_{tj} = \sum\limits_{x_i \in R_{tj}}r_{ti}\bigg / \sum\limits_{x_i \in R_{tj}}|r_{ti}|(1-|r_{ti}|) ctj=xi∈Rtj∑rti/xi∈Rtj∑∣rti∣(1−∣rti∣)
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,二元GBDT分类和GBDT回归算法过程相同。
多元GBDT分类算法:
多元GBDT要比二元GBDT复杂一些,对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K,则此时我们的对数似然损失函数为:
L ( y , f ( x ) ) = − ∑ k = 1 K y k l o g p k ( x ) L(y, f(x)) = - \sum\limits_{k=1}^{K}y_klog\;p_k(x) L(y,f(x))=−k=1∑Kyklogpk(x)
其中如果样本输出类别为k,则 y k = 1 y_k=1 yk=1。第k类的概率pk(x)的表达式为:
p k ( x ) = e x p ( f k ( x ) ) / ∑ l = 1 K e x p ( f l ( x ) ) p_k(x) = exp(f_k(x)) \bigg / \sum\limits_{l=1}^{K} exp(f_l(x)) pk(x)=exp(fk(x))/l=1∑Kexp(fl(x))
集合上两式,我们可以计算出第t轮的第i个样本对应类别l的负梯度误差为:
r t i l = − [ ∂ L ( y i , f ( x i ) ) ) ∂ f ( x i ) ] f k ( x ) = f l , t − 1 ( x ) = y i l − p l , t − 1 ( x i ) r_{til} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f_k(x) = f_{l, t-1}\;\; (x)} = y_{il} - p_{l, t-1}(x_i) rtil=−[∂f(xi)∂L(yi,f(xi)))]fk(x)=fl,t−1(x)=yil−pl,t−1(xi)
观察上式可以看出,其实这里的误差就是样本 i i i对应类别 l l l的真实概率和 t − 1 t−1 t−1轮预测概率的差值。
对于生成的决策树,我们各个叶子节点的最佳残差拟合值为
c t j l = a r g m i n ⎵ c j l ∑ i = 0 m ∑ k = 1 K L ( y k , f t − 1 , l ( x ) + ∑ j = 0 J c j l I ( x i ∈ R t j ) ) c_{tjl} = \underbrace{arg\; min}_{c_{jl}}\sum\limits_{i=0}^{m}\sum\limits_{k=1}^{K} L(y_k, f_{t-1, l}(x) + \sum\limits_{j=0}^{J}c_{jl} I(x_i \in R_{tj})) ctjl=cjl argmini=0∑mk=1∑KL(yk,ft−1,l(x)+j=0∑JcjlI(xi∈Rtj))
由于上式比较难优化,我们一般使用近似值代替:
c t j l = K − 1 K ∑ x i ∈ R t j l r t i l ∑ x i ∈ R t i l ∣ r t i l ∣ ( 1 − ∣ r t i l ∣ ) c_{tjl} = \frac{K-1}{K} \; \frac{\sum\limits_{x_i \in R_{tjl}}r_{til}}{\sum\limits_{x_i \in R_{til}}|r_{til}|(1-|r_{til}|)} ctjl=KK−1xi∈Rtil∑∣rtil∣(1−∣rtil∣)xi∈Rtjl∑rtil
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。
3、XGBoost 算法
- XGBoost 是改进的梯度提升(GB)算法;
- XGBoost 库是 XGBoost 算法的高效实现。
XGBoost 与 GB 的主要区别
- 首先,定义一棵树 f ( x ) f(x) f(x)为:

Here w is the vector of scores on leaves, q is a function assigning each data point to the corresponding leaf, and T is the number of leaves.
-
使用牛顿法代替梯度下降法寻找最优解
前者使用一阶+二阶导数作为残差,后者只使用了一阶导数
This formula can be decomposed as
1). the score on the new left leaf
2). the score on the new right leaf
3). The score on the original leaf
4). regularization on the additional leaf.
这同时也起到了“剪枝”的作用——如果分数小于γ,则不会增加分支;
XGBoost 的一些内部优化
- 在寻找最佳分割点时,传统的方法会枚举每个特征的所有可能切分点。XGBoost 实现了一种近似的算法,大致的思想是根据
百分位法列举几个可能成为分割点的候选者,然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。 - XGBoost 考虑了训练数据为稀疏值的情况,可以为缺失值或者指定的值指定分支的默认方向,这能大大提升算法的效率,paper 提到能提高 50 倍。
特征列排序后以块的形式存储在内存中,在迭代中可以重复使用;虽然 Boosting 算法迭代必须串行,但是在处理每个特征列时可以做到并行。- 按照特征
列方式存储能优化寻找最佳的分割点,但是当以行计算梯度数据时会导致内存的不连续访问,严重时会导致 cache miss,降低算法效率。Paper 中提到,可先将数据收集到线程内部的 buffer,然后再计算,提高算法的效率。 - XGBoost 还考虑了数据量比较大的情况,当内存不够时怎么有效的使用磁盘,主要是结合多线程、数据压缩、分片的方法,尽可能的提高算法的效率。
xgboost的优势:
1、正则化
标准GBM的实现没有像XGBoost这样的正则化步骤。正则化对减少过拟合也是有帮助的。
实际上,XGBoost以“正则化提升(regularized boosting)”技术而闻名。
2、并行处理
XGBoost可以实现并行处理,相比GBM有了速度的飞跃,LightGBM也是微软最新推出的一个速度提升的算法。 XGBoost也支持Hadoop实现。
3、高度的灵活性
XGBoost 允许用户定义自定义优化目标和评价标准 。
4、缺失值处理
XGBoost内置处理缺失值的规则。用户需要提供一个和其它样本不同的值,然后把它作为一个参数传进去,以此来作为缺失值的取值。XGBoost在不同节点遇到缺失值时采用不同的处理方法,并且会学习未来遇到缺失值时的处理方法。
5、剪枝
当分裂时遇到一个负损失时,GBM会停止分裂。因此GBM实际上是一个贪心算法。XGBoost会一直分裂到指定的最大深度(max_depth),然后回过头来剪枝。如果某个节点之后不再有正值,它会去除这个分裂。
这种做法的优点,当一个负损失(如-2)后面有个正损失(如+10)的时候,就显现出来了。GBM会在-2处停下来,因为它遇到了一个负值。但是XGBoost会继续分裂,然后发现这两个分裂综合起来会得到+8,因此会保留这两个分裂。
6、内置交叉验证
XGBoost允许在每一轮boosting迭代中使用交叉验证。因此,可以方便地获得最优boosting迭代次数。
而GBM使用网格搜索,只能检测有限个值。
7、在已有的模型基础上继续
XGBoost可以在上一轮的结果上继续训练。
sklearn中的GBM的实现也有这个功能,两种算法在这一点上是一致的。
参考:
《统计学习方法》李航
GBDT实例详解
推荐博客:
机器学习算法GBDT



