【吴恩达机器学习】第五周课程精简笔记——代价函数和反向传播
Cost Function and Backpropagation(代价函数和反向传播)
1. Cost Function
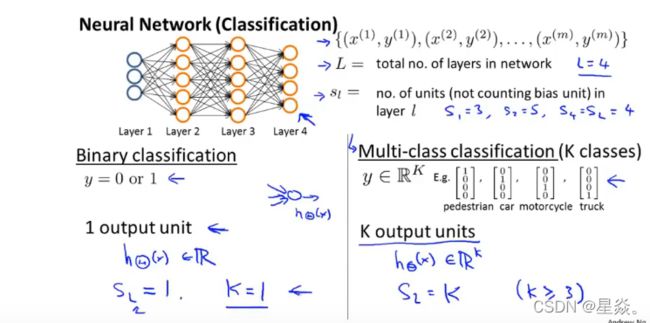
Let’s first define a few variables that we will need to use:
- L = total number of layers in the network
- sl = number of units (not counting bias unit) in layer l
- K = number of output units/classes
- h Θ ( x ) k h_{\Theta}(x)_k hΘ(x)k is being as a hypothesis that results in the kth output.
Recall that the cost function for regularized logistic regression was:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1} [y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m} \sum^n_{j=1} \theta^2_j J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2

For neural networks, it is going to be slightly more complicated:
J ( θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K [ y k ( i ) l o g ( h θ ( x ( i ) ) k ) + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1}\sum^K_{k=1} [y^{(i)}_klog(h_\theta(x^{(i)})_k)+(1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)] + \frac{\lambda}{2m} \sum^{L-1}_{l=1}\sum^{sl}_{i=1}\sum^{sl+1}_{j=1} (\Theta^{(l)}_{j,i})^2 J(θ)=−m1i=1∑mk=1∑K[yk(i)log(hθ(x(i))k)+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
We have added a few nested summations to account for our multiple output nodes. In the first part of the equation, before the square brackets, we have an additional nested summation that loops through the number of output nodes. K here means there are K units of output. That is the final layer of neural network.
In the regularization part, after the square brackets, we must account for multiple theta matrices. The number of columns in our current theta matrix is equal to the number of nodes in our current layer (including the bias unit). The number of rows in our current theta matrix is equal to the number of nodes in the next layer (excluding the bias unit). As before with logistic regression, we square every term.
Note:
- the double sum simply adds up the logistic regression costs calculated for each cell in the output layer.
- the triple sum simply adds up the squares of all the individual Θs in the entire network.
- the i in the triple sum does not refer to training example i.
让我们首先定义一些我们需要用到的变量:
- L = 网络中全部层数
- sL= 第L层的神经元个数(偏置单元不算在内)
- 输出单元/类别个数
- h Θ ( x ) k h_{\Theta}(x)_k hΘ(x)k 作为第k个输出的假设结果
回想一下正则化对数几率回归的代价函数:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1} [y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m} \sum^n_{j=1} \theta^2_j J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
对于神经网络,它会稍微复杂一些:
J ( θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K [ y k ( i ) l o g ( h θ ( x ( i ) ) k ) + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1}\sum^K_{k=1} [y^{(i)}_klog(h_\theta(x^{(i)})_k)+(1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)] + \frac{\lambda}{2m} \sum^{L-1}_{l=1}\sum^{sl}_{i=1}\sum^{sl+1}_{j=1} (\Theta^{(l)}_{j,i})^2 J(θ)=−m1i=1∑mk=1∑K[yk(i)log(hθ(x(i))k)+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
我们添加了一些嵌套的求和来说明我们的多个输出节点。在方程的第一部分,方括号之前,我们有一个额外的嵌套求和,它循环遍历输出节点的数量。这里的K意味着有K个输出单元,也就是神经网络的最后一层。
在正则化部分,方括号之后,我们必须考虑多个矩阵。当前矩阵中的列数等于当前层(包括偏置单元)中的节点数。当前矩阵的行数等于下一层的节点数(不包括偏置单元)。和以前使用逻辑回归时一样,我们将每一项平方。
注意:
- 双求和只是将输出层中每个单元计算出的对数几率回归的代价相加
- 三重求和只是将整个网络中各个 θ \theta θ取平方后相加。
- 三重求和中的i并不指训练样例i.
2. Backpropagation Algorithm
“Backpropagation” is neural-network terminology for minimizing our cost function, just like what we were doing with gradient descent in logistic and linear regression. Our goal is to compute:
m i n Θ J ( Θ ) min_{\Theta} J(\Theta) minΘJ(Θ)
That is, we want to minimize our cost function J using an optimal set of parameters in theta. In this section we’ll look at the equations we use to compute the partial derivative of J(Θ):
∂ J ( Θ ) ∂ Θ i , j ( l ) \frac{\partial J(\Theta)}{\partial \Theta^{(l)}_{i,j}} ∂Θi,j(l)∂J(Θ)
To do so, we use the following algorithm:

Backpropagation Algorithm
Given training set { ( x ( 1 ) , y ( 1 ) ) ⋯ ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}) \cdots (x^{(m)},y^{(m)}) \} {(x(1),y(1))⋯(x(m),y(m))}
- set Δ i , j ( l ) : = 0 \Delta^{(l)}_{i,j}:=0 Δi,j(l):=0 for all (l,i,j), (hence you end up having a matrix full of zeros)
For training example t = 1 to m:
-
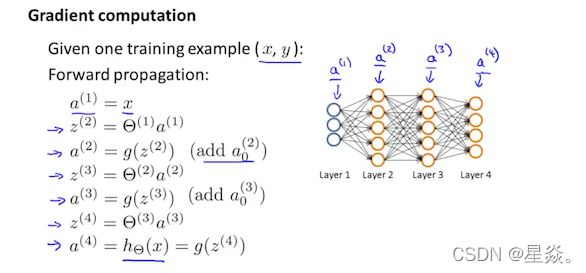
Set a ( 1 ) : = x ( t ) a^{(1)}:=x^{(t)} a(1):=x(t)
-
Using y ( t ) y^{(t)} y(t), compute δ ( L ) = a ( L ) − y ( t ) \delta^{(L)}=a^{(L)}-y^{(t)} δ(L)=a(L)−y(t)
Where L is our total number of layers and a ( L ) a^{(L)} a(L) is the vector of outputs of the activation units for the last layer. So our “error values” for the last layer are simply the differences of our actual results in the last layer and the correct outputs in y.To get the delta values of the layers before the last layer, we can use an equation that steps us back from right to left: -
Compute δ ( L − 1 ) , δ ( L − 2 ) , . . . , δ 2 , \delta^{(L-1)},\delta^{(L-2)},...,\delta^{2}, δ(L−1),δ(L−2),...,δ2, using δ ( l ) = ( ( Θ ( l ) ) T δ ( l + 1 ) ) . ∗ a ( l ) . ∗ ( 1 − a ( l ) ) \delta^{(l)}=((\Theta^{(l)})^T\delta^{(l+1)}).*a^{(l)}.*(1-a^{(l)}) δ(l)=((Θ(l))Tδ(l+1)).∗a(l).∗(1−a(l))
The delta values of layer l are calculated by multiplying the delta values in the next layer with the theta matrix of layer l. We then element-wise multiply that with a function called g’, or g-prime, which is the derivative of the activation function g evaluated with the input values given by z ( l ) z^{(l)} z(l).The g-prime derivative terms can also be written out as:
g ′ ( z ( l ) ) = a ( l ) . ∗ ( 1 − a ( l ) ) ( 1 1 + e − x ) ′ = 1 1 + e − x . ∗ ( 1 − 1 1 + e − x ) g'(z^{(l)}) = a^{(l)}.*(1-a^{(l)}) \\ (\frac{1}{1+e^{-x}})' = \frac{1}{1+e^{-x}}.*(1-\frac{1}{1+e^{-x}}) g′(z(l))=a(l).∗(1−a(l))(1+e−x1)′=1+e−x1.∗(1−1+e−x1) -
Δ i , j ( l ) : = Δ i , j ( l ) + a j ( l ) δ i ( l + 1 ) \Delta^{(l)}_{i,j} := \Delta^{(l)}_{i,j}+a^{(l)}_j\delta^{(l+1)}_i Δi,j(l):=Δi,j(l)+aj(l)δi(l+1) or with vectorization, Δ ( l ) : = Δ ( l ) + δ ( l + 1 ) ( a ( l ) ) T \Delta^{(l)} := \Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T Δ(l):=Δ(l)+δ(l+1)(a(l))T
Hence we update our new Δ \Delta Δ matrix.- D i , j ( l ) : = 1 m ( Δ i , j ( l ) + λ Θ i , j ( l ) ) D^{(l)}_{i,j} := \frac{1}{m}(\Delta^{(l)}_{i,j}+\lambda\Theta^{(l)}_{i,j}) Di,j(l):=m1(Δi,j(l)+λΘi,j(l)), if j ≠ 0
- D i , j ( l ) : = 1 m Δ i , j ( l ) D^{(l)}_{i,j} := \frac{1}{m}\Delta^{(l)}_{i,j} Di,j(l):=m1Δi,j(l), if j = 0
The capital-delta matrix D is used as an “accumulator” to add up our values as we go along and eventually compute our partial derivative. Thus we get ∂ J ( Θ ) ∂ Θ i j ( l ) = D i j ( l ) \frac{\partial J(\Theta)}{\partial\Theta^{(l)}_{ij}}=D^{(l)}_{ij} ∂Θij(l)∂J(Θ)=Dij(l)
“反向传播”是神经网络术语,用于最小化我们的代价函数,就像在对数几率回归和线性回归中做的梯度下降一样。我们的目标是计算:
m i n Θ J ( Θ ) min_{\Theta} J(\Theta) minΘJ(Θ)
也就是说,我们想要使用一组 Θ \Theta Θ的最优参数集来最小化我们的代价函数J。在这一部分,我们将会看到我们使用计算J(Θ) 的偏导数的方程:
∂ J ( Θ ) ∂ Θ i , j ( l ) \frac{\partial J(\Theta)}{\partial \Theta^{(l)}_{i,j}} ∂Θi,j(l)∂J(Θ)
为此,我们使用一下算法:

反向传播算法
对于给定的训练集 { ( x ( 1 ) , y ( 1 ) ) ⋯ ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}) \cdots (x^{(m)},y^{(m)}) \} {(x(1),y(1))⋯(x(m),y(m))}
- 对所有的 (l,i,j),设置 Δ i , j ( l ) : = 0 \Delta^{(l)}_{i,j}:=0 Δi,j(l):=0 , (因此你最后得到一个全部为0的矩阵),其中 Δ \Delta Δ 是大写的 δ \delta δ。
对于训练集 t = 1 to m:
-
Set a ( 1 ) : = x ( t ) a^{(1)}:=x^{(t)} a(1):=x(t)
-
使用 y ( t ) y^{(t)} y(t), 计算 δ ( L ) = a ( L ) − y ( t ) \delta^{(L)}=a^{(L)}-y^{(t)} δ(L)=a(L)−y(t)
这里的L为总层数, a L a^{L} aL 是最后一层激活单元的输出向量。因此最后一层的实际结果与y中正确输出(结果)之差是我们最后一层的“ 误差值 δ \delta δ ”。 δ ( L ) \delta^{(L)} δ(L) 表示第L层的误差。为了得到最后一层之前各层里的 δ \delta δ 值,我们可以使用一个从右至左的方程:
-
通过使用 δ ( l ) = ( ( Θ ( l ) ) T δ ( l + 1 ) ) . ∗ a ( l ) . ∗ ( 1 − a ( l ) ) \delta^{(l)}=((\Theta^{(l)})^T\delta^{(l+1)}).*a^{(l)}.*(1-a^{(l)}) δ(l)=((Θ(l))Tδ(l+1)).∗a(l).∗(1−a(l)),计算 δ ( L − 1 ) , δ ( L − 2 ) , . . . , δ 2 \delta^{(L-1)},\delta^{(L-2)},...,\delta^{2} δ(L−1),δ(L−2),...,δ2
通过将第 l+1层的 δ \delta δ 值与第 l 层的 Θ \Theta Θ 矩阵相乘,得到第 l 层的 δ \delta δ值。然后,用一个叫做 g’ 的函数乘以它,其中g’是激活函数g的导数,由 z ( l ) z^{(l)} z(l) 给出的输入值求解。g '导数项也可以写成:
g ′ ( z ( l ) ) = a ( l ) . ∗ ( 1 − a ( l ) ) ( 1 1 + e − x ) ′ = 1 1 + e − x . ∗ ( 1 − 1 1 + e − x ) g'(z^{(l)}) = a^{(l)}.*(1-a^{(l)}) \\ (\frac{1}{1+e^{-x}})' = \frac{1}{1+e^{-x}}.*(1-\frac{1}{1+e^{-x}}) g′(z(l))=a(l).∗(1−a(l))(1+e−x1)′=1+e−x1.∗(1−1+e−x1) -
Δ i , j ( l ) : = Δ i , j ( l ) + a j ( l ) δ i ( l + 1 ) \Delta^{(l)}_{i,j} := \Delta^{(l)}_{i,j}+a^{(l)}_j\delta^{(l+1)}_i Δi,j(l):=Δi,j(l)+aj(l)δi(l+1) 或者向量化后的 Δ ( l ) : = Δ ( l ) + δ ( l + 1 ) ( a ( l ) ) T \Delta^{(l)} := \Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T Δ(l):=Δ(l)+δ(l+1)(a(l))T
因此我们更新我们的 Δ \Delta Δ 矩阵。- D i , j ( l ) : = 1 m ( Δ i , j ( l ) + λ Θ i , j ( l ) ) D^{(l)}_{i,j} := \frac{1}{m}(\Delta^{(l)}_{i,j}+\lambda\Theta^{(l)}_{i,j}) Di,j(l):=m1(Δi,j(l)+λΘi,j(l)), if j ≠ 0
- D i , j ( l ) : = 1 m Δ i , j ( l ) D^{(l)}_{i,j} := \frac{1}{m}\Delta^{(l)}_{i,j} Di,j(l):=m1Δi,j(l), if j = 0
大写的矩阵D在计算过程中被作为“累加器”使用, 累加我们的值,并最终计算出我们的偏导数。因此,我们可以得到 ∂ J ( Θ ) ∂ Θ i j ( l ) = D i j ( l ) \frac{\partial J(\Theta)}{\partial\Theta^{(l)}_{ij}}=D^{(l)}_{ij} ∂Θij(l)∂J(Θ)=Dij(l)
3. Backpropagation Intution
The following figure shows the process diagram of forward propagation algorithm.
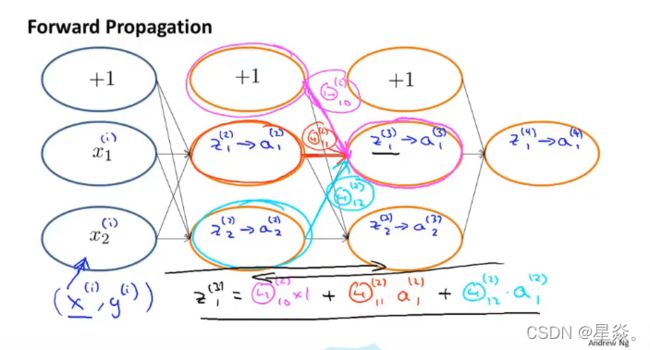
Recall that the cost function for a neural network is:
J ( θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K [ y k ( i ) l o g ( h θ ( x ( i ) ) k ) + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1}\sum^K_{k=1} [y^{(i)}_klog(h_\theta(x^{(i)})_k)+(1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)] + \frac{\lambda}{2m} \sum^{L-1}_{l=1}\sum^{sl}_{i=1}\sum^{sl+1}_{j=1} (\Theta^{(l)}_{j,i})^2 J(θ)=−m1i=1∑mk=1∑K[yk(i)log(hθ(x(i))k)+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
If we consider simple non-multiclass classification(k = 1) and disregard regularization, the cost is computed with:
c o s t ( t ) = y ( t ) l o g ( h Θ ( x ( t ) ) ) + ( 1 − y ( t ) ) l o g ( 1 − h Θ ( x ( t ) ) ) cost(t) = y^{(t)}log(h_\Theta(x^{(t)}))+(1-y^{(t)})log(1-h_\Theta(x^{(t)})) cost(t)=y(t)log(hΘ(x(t)))+(1−y(t))log(1−hΘ(x(t)))
Intuitively, δ j ( l ) \delta^{(l)}_j δj(l) is the “error” for a j ( l ) a^{(l)}_j aj(l) (unit j in layer l). More formally, the delta values are actually the derivate of the cost funcion:
δ j ( l ) = ∂ c o s t ( t ) ∂ z j ( l ) \delta^{(l)}_j = \frac{\partial cost(t)}{\partial z^{(l)}_j} δj(l)=∂zj(l)∂cost(t)
Recall that our derivative is the slope of a line tangent to the cost funcion, so the steeper the slope the more incorrect we are. Let us consider the following neural network below and see how we could calculate some δ j ( l ) \delta^{(l)}_j δj(l):

In the image above, to calculate δ 2 ( 2 ) \delta^{(2)}_2 δ2(2), we multiply the weights Θ 12 ( 2 ) \Theta^{(2)}_{12} Θ12(2) and Θ 22 ( 2 ) \Theta^{(2)}_{22} Θ22(2) by their respective δ \delta δ values found to the right of each edge. So we get δ 2 ( 2 ) = Θ 12 ( 2 ) ∗ δ 1 ( 3 ) + Θ 22 ( 2 ) ∗ δ 2 ( 3 ) \delta_2^{(2)} = \Theta^{(2)}_{12} * \delta^{(3)}_1 + \Theta^{(2)}_{22} * \delta^{(3)}_2 δ2(2)=Θ12(2)∗δ1(3)+Θ22(2)∗δ2(3). To calculate every single possible δ j ( l ) \delta^{(l)}_j δj(l), we could start from the right of our diagram. We can think of our edges as our Θ i j \Theta_{ij} Θij. Going from right to left, to calculate the values of δ j ( l ) \delta^{(l)}_j δj(l), you can just take the over all sum of each weight times the δ \delta δ it is coming from. Hence, another example would be δ 2 ( 3 ) = Θ 12 ( 2 ) ∗ δ 1 ( 4 ) \delta^{(3)}_2 = \Theta^{(2)}_{12}*\delta^{(4)}_1 δ2(3)=Θ12(2)∗δ1(4)
回想一下神经网络的代价函数:
J ( θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K [ y k ( i ) l o g ( h θ ( x ( i ) ) k ) + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(\theta) = - \frac{1}{m} \sum^m_{i=1}\sum^K_{k=1} [y^{(i)}_klog(h_\theta(x^{(i)})_k)+(1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)] + \frac{\lambda}{2m} \sum^{L-1}_{l=1}\sum^{sl}_{i=1}\sum^{sl+1}_{j=1} (\Theta^{(l)}_{j,i})^2 J(θ)=−m1i=1∑mk=1∑K[yk(i)log(hθ(x(i))k)+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
如果我们只考虑非多类别分类(k=1)并且忽视正则化,代价函数便为:
c o s t ( t ) = y ( t ) l o g ( h Θ ( x ( t ) ) ) + ( 1 − y ( t ) ) l o g ( 1 − h Θ ( x ( t ) ) ) cost(t) = y^{(t)}log(h_\Theta(x^{(t)}))+(1-y^{(t)})log(1-h_\Theta(x^{(t)})) cost(t)=y(t)log(hΘ(x(t)))+(1−y(t))log(1−hΘ(x(t)))
凭直觉可发现, δ j ( l ) \delta^{(l)}_j δj(l) 是 a j ( l ) a^{(l)}_j aj(l) (l层的单元j)的误差。更正式的说法, δ \delta δ 实际上是代价函数的导数:
δ j ( l ) = ∂ c o s t ( t ) ∂ z j ( l ) \delta^{(l)}_j = \frac{\partial cost(t)}{\partial z^{(l)}_j} δj(l)=∂zj(l)∂cost(t)
回想一下,我们的导数是代价函数切线的斜率,所以斜率越陡,我们的错误就越大。让我们考虑下面的神经网络并看一看如何计算一些 δ j ( l ) \delta^{(l)}_j δj(l):

在上图中, 为了计算 δ 2 ( 2 ) \delta^{(2)}_2 δ2(2), 我们将 Θ 12 ( 2 ) \Theta^{(2)}_{12} Θ12(2) 和 Θ 22 ( 2 ) \Theta^{(2)}_{22} Θ22(2) 乘上它们在每条边各自右边的 δ \delta δ 值。因此,我们可以得到 δ 2 ( 2 ) = Θ 12 ( 2 ) ∗ δ 1 ( 3 ) + Θ 22 ( 2 ) ∗ δ 2 ( 3 ) \delta_2^{(2)} = \Theta^{(2)}_{12} * \delta^{(3)}_1 + \Theta^{(2)}_{22} * \delta^{(3)}_2 δ2(2)=Θ12(2)∗δ1(3)+Θ22(2)∗δ2(3). 为了计算每一个可能的 δ j ( l ) \delta^{(l)}_j δj(l), 我们可以从图的右边开始。 我们可以把边看作 Θ i j \Theta_{ij} Θij。 从右到左,为了计算 δ j ( l ) \delta^{(l)}_j δj(l) 值, 你可以使用每个权值乘以来自它的 δ \delta δ,再将其求和。因此,另一个例子是 δ 2 ( 3 ) = Θ 12 ( 2 ) ∗ δ 1 ( 4 ) \delta^{(3)}_2 = \Theta^{(2)}_{12}*\delta^{(4)}_1 δ2(3)=Θ12(2)∗δ1(4)。
Backpropagation in Practice
1. Implementation Note: Unrolling Parameters
With neural networks, we are working with sets of matrices:

In order to use optimizaing functions such as “fminuc()”, we will want to “unroll” all the elements and put them into one long vector:
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]
If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11, then we can get back our original matrices from “unrolled” versions as follows:
Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)
在神经网络中,我们使用的是一系列的矩阵:

为了使用像"fminuc()"这样的优化函数,我们需要"展开"所有元素,并将它们放入一个长向量中:
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]
如果Theta1的维数是10x11, Theta2的维数是10x11, Theta3的维数是1x11,那么我们可以从“展开”的版本中得到我们的原始矩阵,如下所示:
Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)
2. Gradient Checking
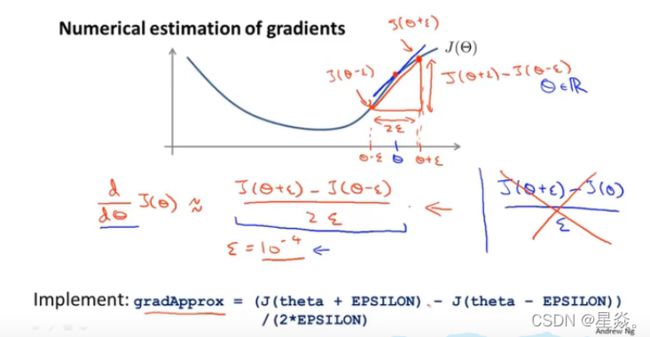
Gradient checking will assure that our backpropagation works as intended. We can approximate the derivative of our cost function with:
∂ J ( Θ ) ∂ Θ ≈ J ( Θ + ϵ ) − J ( Θ − ϵ ) 2 ϵ \frac{\partial J(\Theta)}{\partial\Theta} ≈ \frac{J(\Theta + \epsilon)-J(\Theta - \epsilon)}{2\epsilon} ∂Θ∂J(Θ)≈2ϵJ(Θ+ϵ)−J(Θ−ϵ)
With multiple theta matrices, we can approximate the derivative with respect to Θ j Θ_j Θj as follows:
∂ J ( Θ ) ∂ Θ j ≈ J ( Θ 1 , . . . , Θ j + ϵ , . . . , Θ n ) − J ( Θ 1 , . . . , Θ j − ϵ , . . . , Θ n ) 2 ϵ \frac{\partial J(\Theta)}{\partial\Theta_j} ≈ \frac{J(\Theta_1,...,\Theta_j + \epsilon,... ,\Theta_n)-J(\Theta_1, ...,\Theta_j - \epsilon,...,\Theta_n)}{2\epsilon} ∂Θj∂J(Θ)≈2ϵJ(Θ1,...,Θj+ϵ,...,Θn)−J(Θ1,...,Θj−ϵ,...,Θn)
A small value for ϵ {\epsilon} ϵ such as ϵ = 1 0 − 4 \epsilon = 10^{-4} ϵ=10−4, guarantees that the math works out properly. If the value for ϵ \epsilon ϵ is too small, we can end up with numerical problems.
Hence, we are only adding or subtracting epsilon to the Θ j \Theta_j Θjmatrix. In octave we can do it as follows:
epsilon = 1e-4;
for i = 1:n,
thetaPlus = theta;
thetaPlus(i) += epsilon;
thetaMinus = theta;
thetaMinus(i) -= epsilon;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;
We previously saw how to calculate the deltaVector. So once we compute our gradApprox vector, we can check that gradApprox ≈ deltaVector.
Once you have verified once that your backpropagation algorithm is correct, you don’t need to compute gradApprox again. The code to compute gradApprox can be very slow.

梯度检查将确保我们的反向传播工作如预期。我们可以用以下方法近似代价函数的导数:
∂ J ( Θ ) ∂ Θ ≈ J ( Θ + ϵ ) − J ( Θ − ϵ ) 2 ϵ \frac{\partial J(\Theta)}{\partial\Theta} ≈ \frac{J(\Theta + \epsilon)-J(\Theta - \epsilon)}{2\epsilon} ∂Θ∂J(Θ)≈2ϵJ(Θ+ϵ)−J(Θ−ϵ)
ϵ {\epsilon} ϵ 的一个小值,例如 ϵ = 1 0 − 4 \epsilon = 10^{-4} ϵ=10−4,可以保证数学计算正确。 如果 ϵ \epsilon ϵ 的值太小,我们就会遇到数值问题。
因此,我们只是对 Θ j \Theta_j Θj 矩阵加或减。在Octave我们可以这样做:
epsilon = 1e-4;
for i = 1:n,
thetaPlus = theta;
thetaPlus(i) += epsilon;
thetaMinus = theta;
thetaMinus(i) -= epsilon;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;
我们之前看到了如何计算deltaVector。一旦我们计算了我们的gradApprox向量,我们可以检查gradApprox≈deltaVector。
一旦你验证了你的反向传播算法是正确的,你就不需要再计算gradApprox了。计算gradApprox的代码可能非常慢。

3. Random Initialization
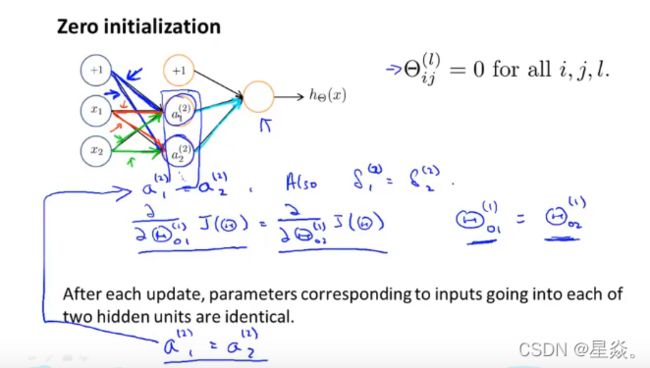
Initializing all theta weights to zero does not work with neural networks. When we backpropagate, all nodes will update to the same value repeatedly. Instead we can randomly initialize our weights for our Θ \Theta Θ matrices using the following method:

Hence, we initialize each Θ i j ( l ) \Theta^{(l)}_{ij} Θij(l) to a random value between [ − ϵ , ϵ ] [-\epsilon,\epsilon] [−ϵ,ϵ]. Using the above formula guarantees that we get the desired bound. The same procedure applies to all the Θ \Theta Θ's. Below is some working code you could use to experiment.
If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
rand(x,y) is just a function in octave that will initialize a matrix of random real numbers between 0 and 1.
(Note: the epsilon used above is unrelated to the epsilon from Gradient Checking)
将所有的权值初始化为零并不适用于神经网络。当我们反向传播时,所有节点将重复更新为相同的值。相反,我们可以使用以下方法随机初始化 Θ \Theta Θ 矩阵的权值:

因此,我们可以将每一个 Θ i j ( l ) \Theta^{(l)}_{ij} Θij(l) 初始化为 [ − ϵ , ϵ ] [-\epsilon,\epsilon] [−ϵ,ϵ] 之间的一个随机值。 使用上面的公式,可以保证我们得到想要的边界。同样的过程适用于所有的 Θ \Theta Θ。下面是一些可以用于实验的工作代码。
If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
rand(x, y)仅是一个在Octave中的函数,它将初始化一个由0到1之间的随机实数组成的矩阵。
(注:上面使用的与梯度检查中的无关)
4. Putting it Together
First, pick a network architecture; choose the layout of your neural network, including how many hidden units in each layer and how many layers in total you want to have.
- Number of input units = dimension of features x ( i ) x^{(i)} x(i)
- Number of output units = number of classes
- Number of hidden units per layer = usually more the better (must balance with cost of computation as it increases with more hidden units)
- Defaults: 1 hidden layer. If you have more than 1 hidden layer, then it is recommended that you have the same number of units in every hidden layer.
Training a Neural Network
- Randomly initialize the weights
- Implement forward propagation to get h Θ ( x ( i ) ) h_\Theta(x^{(i)}) hΘ(x(i)) for any x ( i ) x^{(i)} x(i)
- Implement the cost function
- Implement backpropagation to compute partial derivatives
- Use gradient checking to confirm that your backpropagation works. Then disable gradient checking.
- Use gradient descent or a built-in optmization function to minimize the cost function with the weghts in delta.
When we perform forward and back propagation, we loop on every training example:
for i = 1:m,
Perform forward propagation and backpropagation using example (x(i),y(i))
(Get activations a(l) and delta terms d(l) for l = 2,...,L
The following image gives us an intuition of what is happening as we are implementing our neural network:
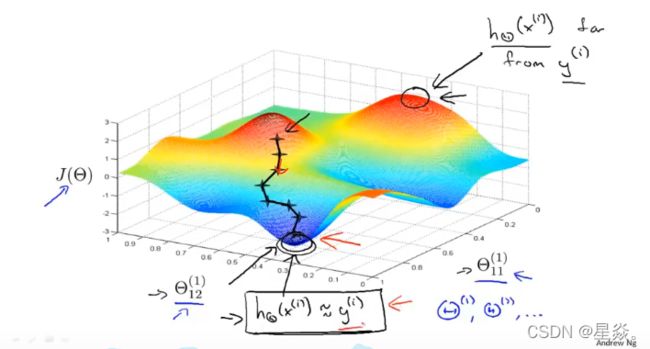
Ideally, you want h Θ ( x ( i ) ) ≈ y ( i ) h_\Theta(x^{(i)})≈y^{(i)} hΘ(x(i))≈y(i). This will minimize our cost function. However, keep in mind that J ( θ ) J(\theta) J(θ) is not convex and thus we can end up in a local minimum instead.
首先,选择一个网络架构; 选择你的神经网络的布局,包括每一层有多少隐藏单元,以及你想要总共有多少层。
- 输入单元个数 = 特征 x ( i ) x^{(i)} x(i) 的维数
- 输出单元个数 = 类别个数
- 每个隐藏层单元的数量 = 通常越多越好(因为计算成本会随着隐藏单元的个数而增加,因此必须与计算成本相平衡)
- 默认值: 1个隐藏层。如果你设置的隐藏层的个数超过一,建议把各个隐藏层中单元个数都设置为相同个数。
训练神经网络
- 随机地初始化权重
- 实现前向传播,对于任意 x ( i ) x^{(i)} x(i)得到 h ( x ( i ) ) h_\ (x^{(i)}) h (x(i))
- 实现代价函数
- 实现反向传播计算偏导数
- 使用梯度检查来确认反向传播是有否效的。 然后禁用梯度检查。
- 使用梯度下降或内置的优化函数来最小化权值为 δ \delta δ 的代价函数。
当我们执行前向和后向传播时,我们对每个训练示例进行循环:
for i = 1:m,
Perform forward propagation and backpropagation using example (x(i),y(i))
(Get activations a(l) and delta terms d(l) for l = 2,...,L
下图让我们直观地了解了在我们实现神经网络的过程中发生了什么:
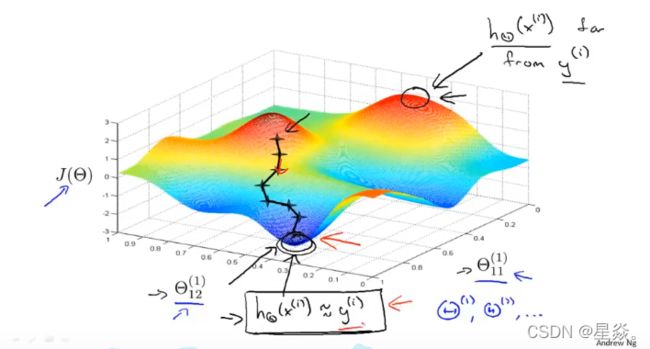
理想情况下,你需要让 h ( x ( i ) ) ≈ y ( i ) h_\ (x^{(i)})≈y^{(i)} h (x(i))≈y(i)。 这样做会使代价函数最小化。 然而,请记住 J ( θ ) J(θ) J(θ) 不是凸(函数)的,因此最终我们得到了一个局部最小值。
Exercise 4:反向传播算法
【吴恩达机器学习】Week5 编程作业ex4——神经网络学习
拓展资料
一文搞懂反向传播算法
反向传播算法(过程及公式推导)
深度学习——以图读懂反向传播
深度学习笔记三:反向传播(backpropagation)算法