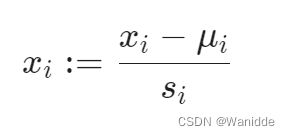吴恩达机器学习——第二周学习笔记
多元线性回归(multivariate linear regression)
多元假设函数:hθ(x)=θ0+θ1X1+θ2X2+θ3X3+⋯+θnXn
其中:X0=1
多元梯度下降(Gradient Descent For Multiple Variables)
多元梯度下降和一元的形式相同,重复求解θj直至收敛。
我们可以通过让每个输入值在大致相同的范围内来加速梯度下降。这是因为θ在小范围内迅速下降,在大范围内缓慢下降,因此当变量非常不均匀时,θ将低效地振荡到最佳值。
想要加快到达最小值的方法就是我们可以修改输入变量的范围。
有两种技术可以帮助实现这一点:特征缩放和均值归一化。
特征放缩(feature scaling)
将特征取值约束到−1到+1的范围内,可以大于或者小于-1 ~ +1,但是也别太大或太小,只要与-1 ~ +1范围偏差不多就可以接受。
均值归一化(mean normalization)
如:Xi代表房价,范围是(100,2000),平均值为1000,则![]() .
.
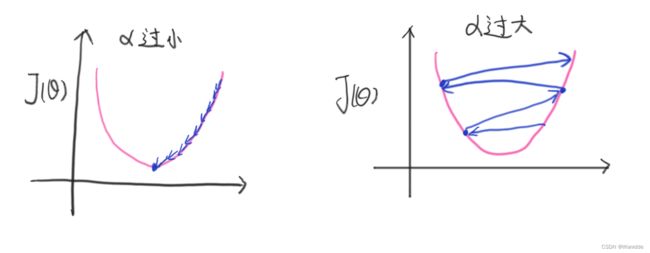
梯度下降的缺点:
α过小:收敛很慢(到达最低点很慢)
α过大:可能会错过最低点
代码:
#均值归一化
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
#梯度下降函数
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
errors = X*theta.T - y
for j in range(parameters):
term = np.multiply(errors, X[:,j])
temp[0,j] = theta[0,j] - alpha*(1/X.shape[0])*np.sum(term)
theta = temp
cost[i] = calculateCost(X, y, theta)
return theta, cost
data2.insert(0, 'Ones', 1)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:cols-1:cols]
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
calculateCost(X2, y2, g2)特征和多项式回归(Features and Polynomial Regression)
线性回归并不适用于所有数据,无法根据我们的已知信息拟合出符合逻辑的点。
所以有时我们需要使用曲线来表达我们的数据,
比如一个二次方模型: ![]()
或者三次方模型:![]()
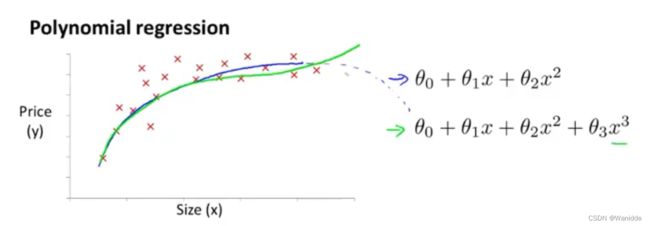
多项式回归能够使用线性回归的方法来拟合非常复杂的函数,甚至是非线性函数。
如:x是房子的尺寸,y是房价,那么我们就无法用二次方程来拟合,因为房价是不会随着面积的增大而减少的,所以就可以采用三次方程来拟合。
如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
正规方程(Normal Equation)
梯度下降是求解代价函数J的最小值,正规方程则是我们求解代价函数J的最小值的第二种方法。
正规方程不需要像梯度下降一样来迭代的求解,而是对θ求导,并令其一阶导等于0,来求解J的最小值。也不用进行特征放缩。
正规方程的公式:![]()
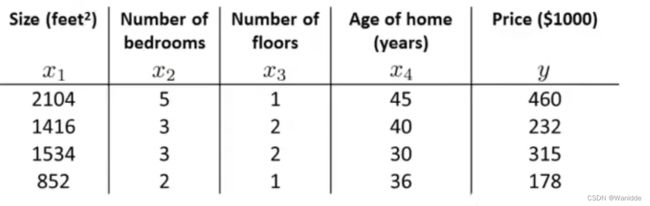
如:
梯度下降和正规方程的比较:
| 梯度下降 | 正规方程 |
| 需要对α进行选择 | 不需要挑选α |
| 需要多次迭代 | 不需要多次迭代 |
| 当n很大时比较适用 | 当n很大时速度会慢(n>10000时) |
但正规方程中![]() 存在不可逆的情况,原因一般如下:
存在不可逆的情况,原因一般如下:
- 有冗余的特征值,即两特征值之间相关
- m<=n
代码:
def normalEquation(X, y):
theta = (X.T*X).I*X.T*y
return theta学习参考:吴恩达机器学习第二周