SPSS参数检验、非参数检验、方差分析

1.导语

在做数据分析的时候，不是只要有数据，就拿去做模型，也有很多数据，结合需求，是不需要用到模型的，比如：

奶茶店，老板想看一下，合作时间（年份为单位）与奶茶店销量的关系与差异。

像这样，只有一个自变量和一个因变量的数据，做模型效果是非常差的，也不能做聚类分析，因为数据上已经使用合作年份做分组了。

如果我们想看下不同自变量因素$X$，或者类别$X_1,X_2...$下，对自变量Y，或者$Y_1,Y_2,..$的关系差异情况，就可以用到二种方法：

• 参数检验
• 非参数检验

这个关系差异分析：可以像聚类分析，那样，每一个聚类分布的聚类中心都可以作为这个聚类数据分布的统计参数值，对比这几个聚类特征的统计参数值，即可看出其中的关系和差异。

如果我们想看下不同自变量因素$X$，或者类别$X_1,X_2...$下，对自变量Y，或者$Y_1,Y_2,..$产生的影响情况，可以用方差分析

2.参数检验

参数检验是根据样本数据推断总体特征的方法，在样本数据基础上，以概率形式对统计总体未知的数量特征（如均值，方差）进行表述

通过样本推断总体，有二个原因：

1. 总体数据无法收集
2. 总体数据收集耗费成本过高

前面已经提到了总体分布已知与未知选择什么检验方法，如果你有总体的数据，可以通过直方图，或者正态性检验等方法来检验数据分布

但大部分情况我们是没有总体数据的，需要对我们分析的数据现象进行分析了，对我们的数据（随机变量）进行数据分布分析

2.1 数据分布

既然要判断总体分布，那首先我们先了解一下有哪些数据分布，以及对应分布的统计参数。

随机变量分为两类：离散型随机变量和连续型随机变量

离散型随机变量是指它全部的取值是有限个或可列无限多个
连续型随机变量是指在某一段区间上可以取无限多个数值的随机变量

连续与离散的区别：
变量按其数值表现是否连续。变量值的变动幅度不同。对离散变量，如果变量值的变动幅度小，就可以一个变量值对应一组，称单项式分组。

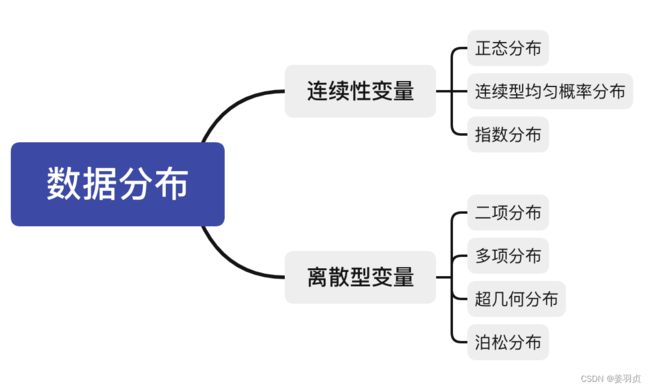
最常见的数据分布有：

• 正态分布
• 指数分布

这里就只介绍连续型变量的数据分布下，如果检验是否为这个分布，以及这个数据分布下，看那些统计参数。

检验数据分布分二种：

• 一种是自己有总体数据，在SPSS用P-P图检验总体数据的分布
• 一种是没有自己总体数据，用抽样数据去做非参数检验

P-P图

非参数

2.1.1 正态分布

1.有总体数据

1.图示法
1.P-P图
2.Q-Q图
3.直方图
4.箱式图
5.茎叶图

2.计算法
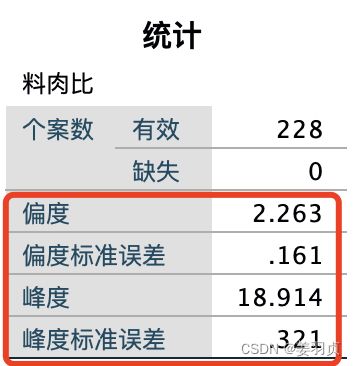
用偏度系数，峰度系数来定量判断，最实用

用数据其分布的：偏度值、偏度标准误值，计算Z-score
$$Z-score=偏度值/偏度标准误差值$$

峰度值、峰度标准误差值，计算Z-score
$$Z-score=峰度/峰度标准误差值$$

只有偏度值和峰度值均≈0，Z-score均在±1.96之间，可认为数据服从正态分布

SPSS步骤
1.

2.

3.

2.没有总体数据，用样本

用非参数检验单样本K-S

SPSS步骤
1.

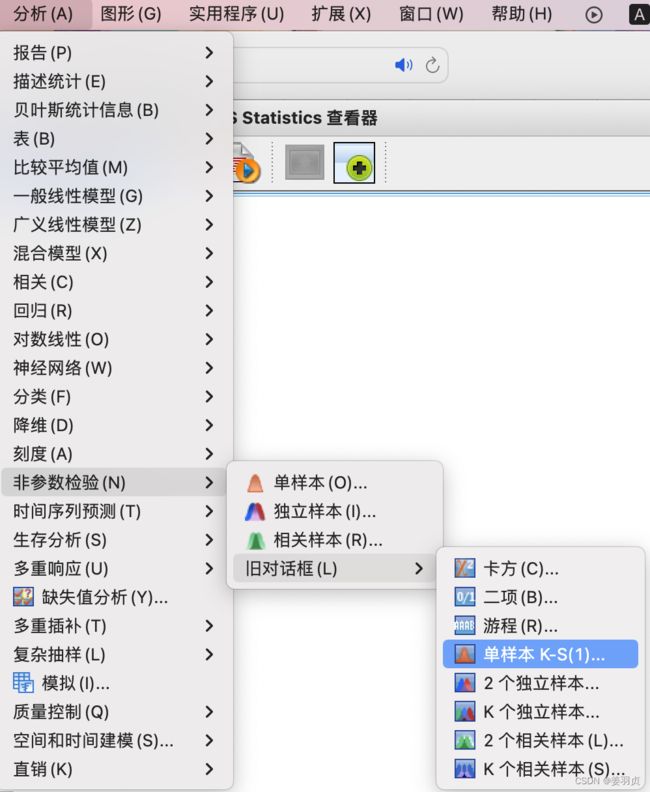
2.

3.

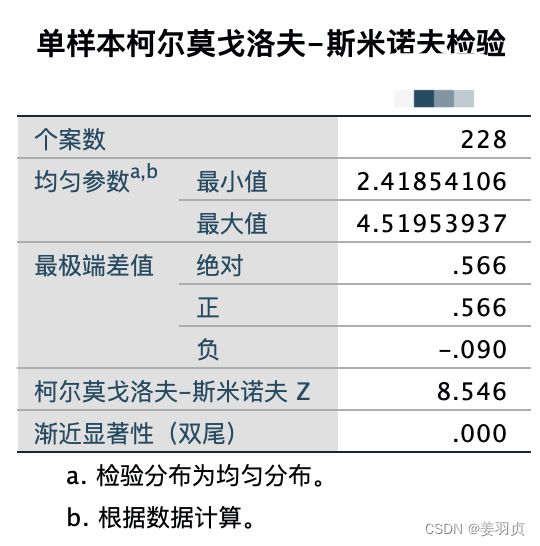
渐近显著性大于0.05表示符合选择检验的这个分布。

3.统计参数

数据为正态分布，具有代表性的参数有均值和方差。

2.1.2 指数分布

1.有总体数据

图示法
1.P-P图
2.Q-Q图

2.没有总体数据，样本

用非参数检验单样本K-S

跟正态分布一样的

3.统计参数

1.指数分布具有代表性的参数：

λ：为单位时间事件发生的次数

统计参数的目的，是用一个固定的值，来代表整个数据的情况，进一步，做不同样本，不同总体之间的差异分析，就是我们常说的参数估计里的点估计。

2.2 单样本t检验

2.2.1 单样本t检验目的

单样本t检验的目的是利用某总体的样本数据，推断该总体的均值与指定检验值间的差异在统计，它是对总体均值的假设检验

例如：利用商品房意向的抽样调查数据，推断月住房开销总体平均值是否为2000元

虽然抽样会存在误差，但是样本均值的抽样分布是可以确定的，比如抽样t分布等。当总体分布为正态分布，样本均值的抽样分布仍为正态分布。

2.2.2 SPSS操作

选项【分析->比较均值->单样本T检验】

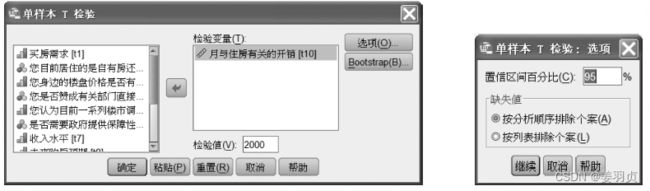
例如：
利用商品购买意向调查数据，推断被访者月住房总体平均值是否为2000元，由于该问题涉及是单个总体，且要进行总体均值检验，同时月开销总体近似服从正态分布，因此，可采用单样本t检验来进行分析，原假设$H_0:u=u_0=2000$

通过SPSS得到如下结果：

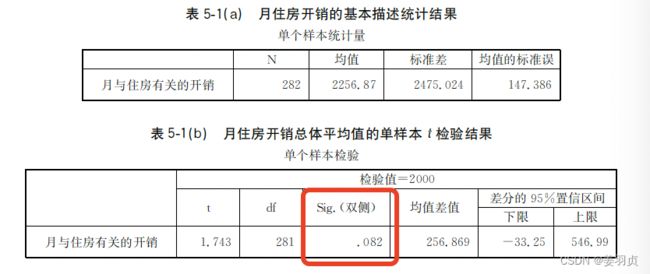
该问题采用双侧检验，从图中得p=0.082大于0.05，因此不能拒绝原假设，认为月住房开销的总体平均值与2000没有显著差异。

2.3 两独立样本t检验

2.3.1 目的

两独立样本t检验的目的是：利用来自两个总体的独立样本，推断两个总体的均值是否存在显著差异。

例如：利用商品房购买意向抽样调查数据，推断居住出租房和自有房的月住房开销总体平均值是否有显著差异

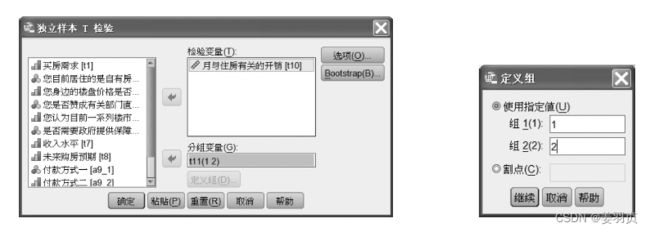
2.3.2 SPSS操作

选项【分析->比较均值->独立样本T检验】

例如：
利用商品购买意向调查数据，分析不同居住类型的月住房开销总体均值是否存在显著差异，原假设是两总体平均值无显著差异，即$H_0:u_1-u_2=0$

通过SPSS得到如下结果：

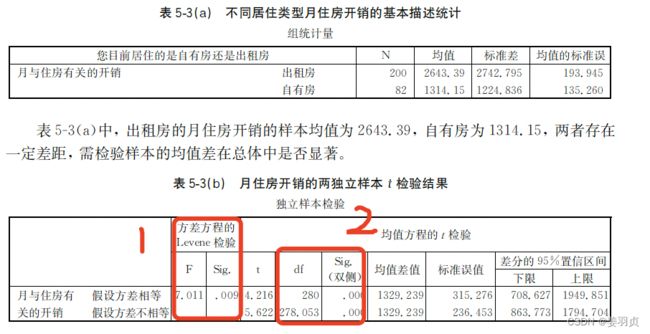
根据上图信息，
第一步，检验两个总体方差齐次性，即是否存在方差显著性差异，如果有，才能进行两个总体样本的均值差异判断

从图中得方差F统计量为7.011，p值为0.009小于0.05，证明两个总体方差存在显著性差异，

第二步,观察t统计量，判断均值是否存在显著差异

从图中得均值t检验，p值为0.000小于0.05，拒绝原假设，认为两个总体均值存在显著差异。

2.4 两配对样本t检验

2.4.1 目的

两配对样本t检验的目的是，利用来自两个总体配对样本，推断两个总体的均值是否存在显著差异

例如：为研究某种减肥茶是否有显著的减肥效果，需要对肥胖人群喝茶前与喝茶后的体重进行分析

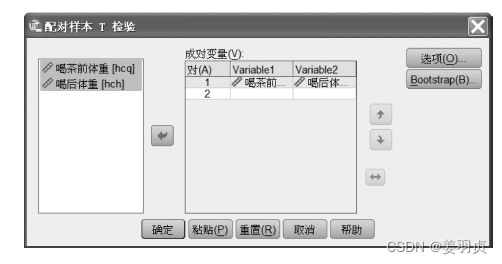
2.4.2 SPSS操作

选项【分析->比较均值->配对样本T检验】

例如：肥胖人群喝茶前与喝茶后的总体平均体重无显著差异，即$H_0:u_1-u_2=0$

通过SPSS得到如下结果：

p接近于0.小于0.05，拒绝原假设，认为喝茶前后体重差有显著不同

3.方差分析

方差分析需要满足三个假设前提：

1. 各总体均服从正态分布
2. 各样本的总体方差相等，即具有方差齐性
3. 各样本互相独立的随机样本

各样本是否相互独立，可以通过一致性卡方检验
https://blog.csdn.net/weixin_42010722/article/details/124296654

3.1 单因素方差分析

3.1.1 目的

单因素方差分析研究一个控制变量的不同水平，是否对观测变量产生显著影响。

例如：不同地区下，广告销售额入是否存在显著影响

3.1.2 SPSS操作

选项【分析->比较均值->单因素ANOVA】

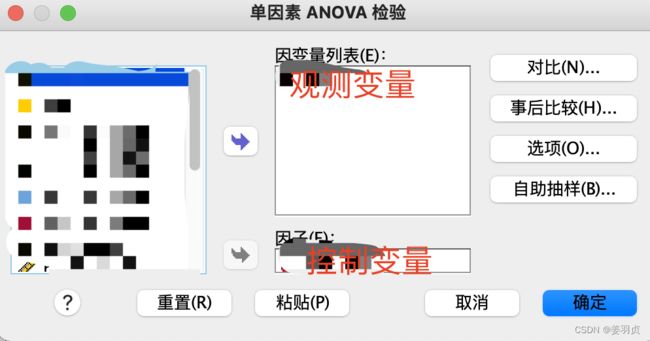
2.勾选选项



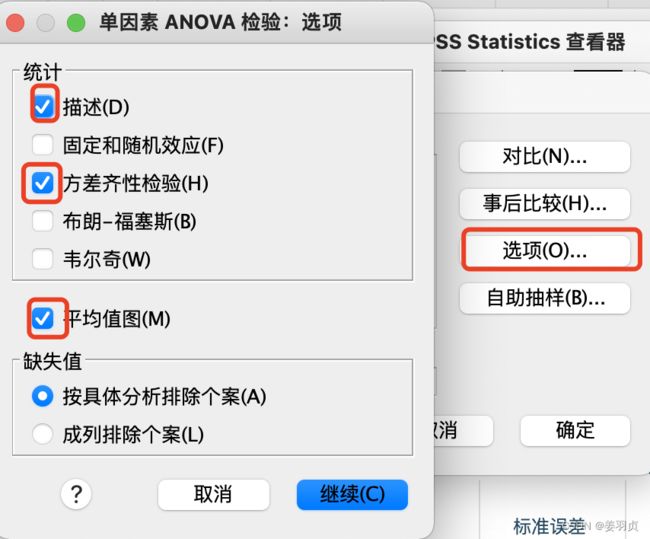
通过SPSS得到结果：

p=0.121 小于0.05 方差无显著差异，则可以进行下一步

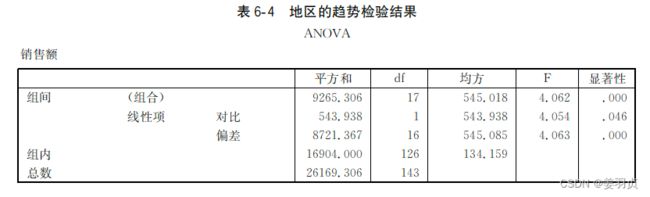
p=0.000 小于0.05，拒绝原假设，不同地区间销售额存在显著差异。

3.2 多因素方差分析

两个或两个以上控制变量是否对观测变量产生影响

备注：关于两个组样本，或多个组样本，在随机抽样中，可能存在样本量不一致的情况，只要满足方差齐性，样本间相互独立，样本服从正态分布即可，至于样本量，没有固定的要求。在于的是检验效果的情况

4.非参数检验

4.1 单样本非参数检验

得到一批样本数据，想知道这个数据的总体服从那一张数据分布呢，这里就用可以用到前面提到的P-P，Q-Q等方法判断，也可以用非参数检验的方法比如：卡方检验，二项分布检验，K-S检验来判断。

4.1.1 总体分布的卡方检验

定义：总体分布的卡方检验适用于配合度检验，是根据样本数据的实际频数推断总体分布与期望分布或理论分布是否有显著差异。
特点：比较适用于一个因素的多项分类数据分析。总体分布的卡方检验的数据是实际收集到的样本数据，而非频数数据。

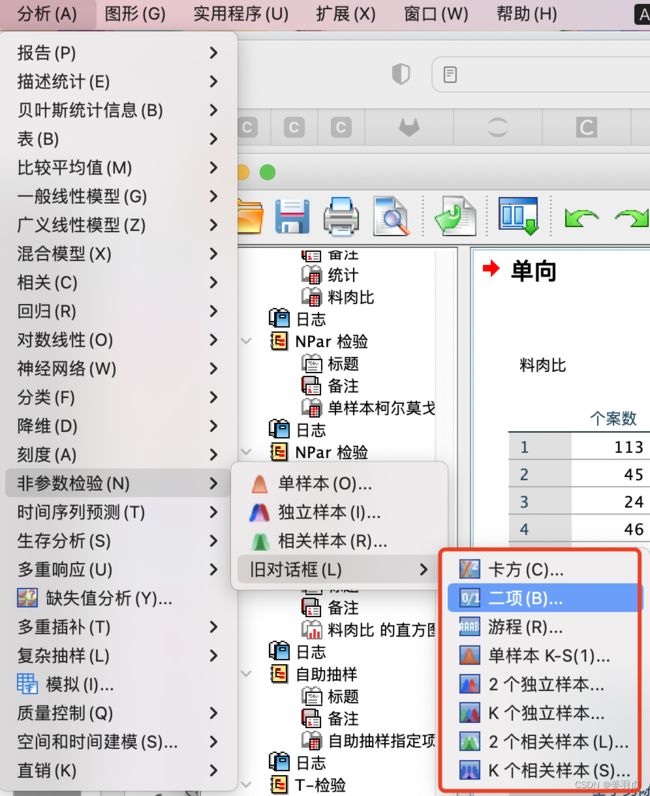
4.1.2 二项分布检验

二项分布：从这种二分类总体中抽取的所有可能结果，要么是对立分类中的这一类，要么是另一类，其频数分布称为二项分布
二项分布检验：SPSS二项分布检验就是根据收集到的样本数据，推断总体分布是否服从某个指定的二项分布

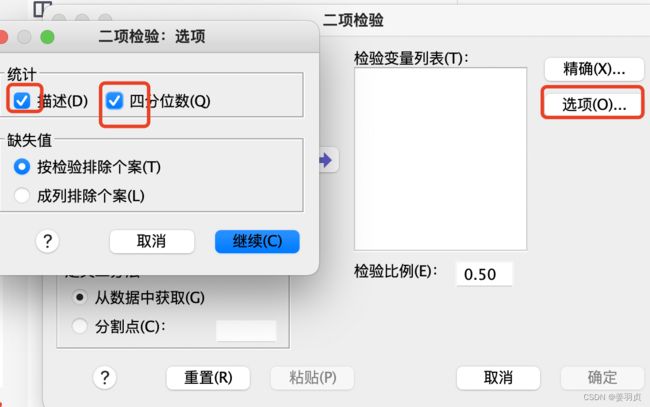
4.1.3 单样本K-S检验

定义：单样本K-S检验是利用样本数据推断总体是否服从某一理论分布的方法，适用于探索连续型随机变量的分布形态

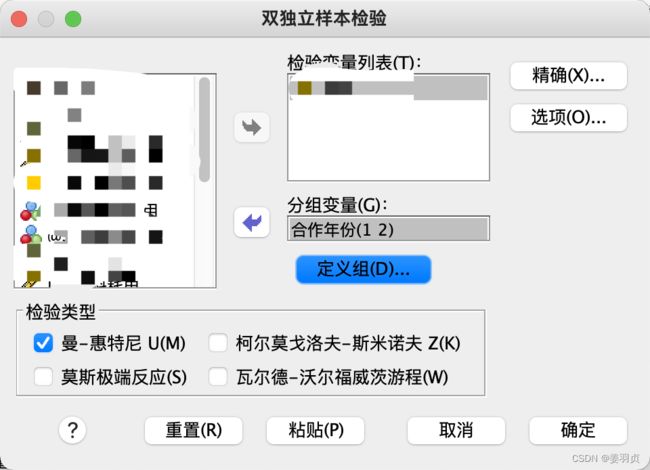
4.2 两独立样本的非参数检验

定义：两独立样本的非参数检验是在对总体分布不很了解的情况下，通过分析样本数据，推断样本来自的两个独立总体分布是否存在显著差异

一般用来对两个独立样本的均数、中位数、离散趋势、偏度等进行差异比较检验。

检验方法：

1. 两独立样本的Mann-Whitney U检验（主要检验总体均值有没有显著差异）
2. 两独立样本的K-S检验
3. 两独立样本的游程检验
4. 两独立样本的极端反应检验

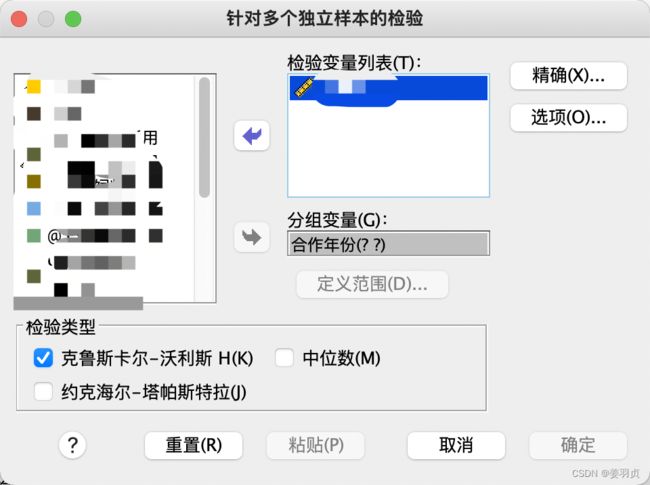
4.3 多独立样本的非参数检验

定义：多独立样本非参数检验分析样本数据是推断样本来自的多个独立总体分布是否存在显著差异

SPSS多独立样本非参数检验一般推断多个独立总体的均值或中位数是否存在显著差异

检验方法：

1. 多独立样本的中位数检验
2. 多独立样本的K-W检验
3. 多独立样本的Jonkheere-Terpstra检验
   

4.4 两配对样本的非参数检验

定义：两配对样本 (2 Related Samples）非参数检验是在对总体分布不很清楚的情况下，对样本来自的两相关配对总体分别进行检验

前提要求：首先两个样本的观察数目相同，其次两样本的观察值顺序不能随意改变

检验方法：

1. 两配对样本的McNemar变化显著性检验（二值数据）
2. 两配对样本的符号 (Sign）检验
3. 两配对样本的Wilcoxon符号平均秩

5 参数检验与非参数检验对比

检验特征对比

分析方法	参数检验	非参数检验
适用范围	正态分布	分布未知
检验效能	高	低
对比指标	平均值	中位数
图像展示	折线图	箱线图

分析方法选择对比

功能	参数	非参数检验
与某一个数字对比	单样本t检验	单样本Wilcoxon检验
两组数据的差异	独立样本t检验	Mann-Whitney检验
多组数据的差异	单因素方差分析	Kruskal-Wallis检验
配对数据差异	配对样本t检验	配对Wilcoxon检验