GBDT(梯度提升决策树)与GBRT(梯度提升回归树)原理详解

学GBDT,GBRT之前要先对梯度下降法有一点了解.下面的链接可以做一定参考
梯度与梯度下降法详解.
GradientBoostingDescitionTree:梯度提升算法(提升树算法),利用梯度下降法求解的Boosting算法.

1提升树的原理

 提升树(BoostingTree)是以决策树为基本学习器的提升方法,其预测性能相当优异.
 (1)对于分类问题:决策树是二叉分类树
 (2)对于回归问题:决策树是二叉回归树
提升树模型:决策树作为基本分类器的加法模型:

M为决策树的数量,θm第m个决策树的参数,hm(x;θm)表示第m个决策树分类器
注意:θm还有一层隐藏含义:
θm的值要使得当前第m步提升树模型fm(x)(累加得到的)的损失函数最小化.而这一过程是通过梯度下降法实现的(梯度下降法求得当前模型的残差,残差拟合出一颗决策树得到θm),所以提升树模型又称为梯度提升算法.(这与之前的Boosting算法是有区别的)

提升树算法采用前向分布算法.令fm-1(x)为前项模型(前m-1个决策树分类器累加得到的),则第m步提升树模型为:
fm(x)=fm-1(x)+hm(x;θm)
其中初始化提升树f0(x)=0
然后通过最小化当前第m步模型的损失函数来确定第m步决策树分类器的θm参数
所以当提升树有N个决策树分类器时,就要求得N个θ参数来使得当前第xxx步模型的损失函数最小化.相当于对损失函数做了N次优化(使得提升树的损失函数的最小值不断的减少)

其中:
argmin 表达式:表示的是使这个表达式最小值时,对应表达式参数组的集合,当表达式只有一个最小值时,为单点集合.
如果使用不同的损失函数,则得到两种不同的提升树算法(真实值为y,预测值为y1)
(1)回归问题:通常使用平方损失函数:

(2)分类问题:通常使用指数损失函数:

用前项分布法,则在第m步给定前项模型,求解:

对于回归问题:采用平方误差损失函数:
得到
r:当前第m步提升树模型拟合数据的残差(yi-fm-1(x),而这个值已经是m-1步损失函数的最小值了(然后用这个前项损失函数的最小值就是为当前模型的残差),对于提升树算法,只需要使用第m颗决策树hm(x;θm)拟合当前模型的残差(利用hm(x;θm)使得这个最小值取到进一步的最小值(找到对应的θm))
补充:
 1.当前模型的残差=前项损失函数的最小值.
总结:拟合前项残差(梯度下降) --> 找到θm --> 找到第m颗决策树 --> 累加前项模型得到当前模型

2 提升树算法

GBDT与GBRT算法:
输入:训练数据集
输出:提升树fM(x) ,其中M的值为决策树分类器个数
算法步骤:
 1 初始化f0(x)=c,给定损失函数(c的的取值可以使得第0步模型的损失函数取最小值)
 2 对于m=1,2…M
  计算残差rm=yi-fm-1(x),i=1,2…N(用前项模型残差近似替代的)
  拟合残差rm学习一颗回归树(决策树分类器),得到hm(x;θm)(求得θm的值)使得损失函数最小化(残差变小)
  更新提升树:fm(x)=fm-1(x)+hm(x;θm)
3 得到提升树:

用上面的步骤解决分类问题:GBDT
      解决回归问题:GBRT

3GBDT与GBRT

 提升是一个机器学习技术,可用于解决分类与回归问题,它每一步产生一个弱预测模型,如决策树,并加权累加到总模型中,如果每一步弱预测模型的生成都是依据损失函数的梯度方向(求解θ),则称之为梯度提升.
 梯度提升算法首先给定一个损失函数(目标函数),它的定义域是所有可行的弱函数集合(基函数),提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值
 提升的理论意义:如果一个问题存在弱分类器,则可以通过提升的方式得到强分类器
 在提升树的基础上,利用梯度下降法,求解目标函数或者损失函数的最优情况,就称之为梯度提升算法.
 提升树中,如果损失函数是平方损失函数和指数损失函数时,由于这两种函数求导更简单,所以求解下面的参数最优解就比较简单了.

 如果损失函数是一般函数,该优化问题往往比较难求得,Freidman提出了梯度提升算法来解决该最优值求解的问题–利用损失函数的负梯度(梯度下降法)在前项模型的值作为当前提升树算法中残差的近似值,拟合一颗决策树.在回归问题中,这称之为梯度提升回归树GBRT,在分类问题中,称之为梯度提升决策树GBDT;
梯度提升决策树算法总结:
 多个决策树/回归树分类器的组合;
 首先要确定损失函数与初始化决策树分类器f0(x)=0
 第m步决策树分类器的参数θm使得到当前第m步梯度提升模型的损失函数最小化
 参数θm是通过梯度下降法求得的残差间接得到的
 而最小化损失函数的过程是根据提升树中决策树分类器个数而不断重复的过程(相当于对损失函数做了多次优化,多次求解极小值)
 对于残差的理解:前一步提升树所遗留下来的损失值(m-1步的损失函数的最小值),然后通过当前步的决策树分类器做进一步的减小.
GBDT/GBRT与AdaBoost算法的区别:
 都是集成学习的串行方式
 但GBDT/GBRT在Boosting算的基础上,做了两点改进:
  1使用决策树/回归树算法,而AdaBoost使用的是各种算法(二分类)
  2使用梯度下降法降低损失函数,而AdaBoost使用的是样本的权值与分类器的线性组合来降低损失函数

梯度提升回归树算法的详细步骤如下:
输入训练数据集:
输出:回归树fM(x)
1 初始化提升树:

注:这是一颗只有根节点的树(所有样本都在根节点中做了决策,属于什么类别),根节点的类别(指常数c)为使得损失函数值最小

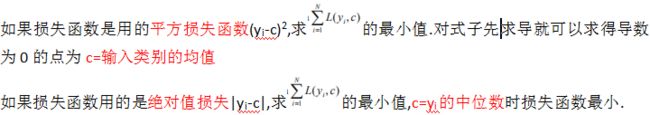
2对于m=1,2…M指的是串行分类器的个数
 A对于i=1,2…N指的是求残差时yi与f(xi)中i的值

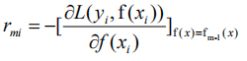
 中括号表示的是梯度,说明他这里在用梯度下降法求解前项模型的残差,然后用前项模型的残差的最小值作为当前模型的残差(因为当前模型都没有算出来,没有办法计算残差yi-fm(xi),fm(xi)未知)
 这个公式说明可利用这个公式求得前项模型的残差的最小值作为当前模型的残差(再用第m颗决策树拟合它)
 B用rmj拟合一颗回归树,得到第m颗树的叶子节点区域Rmj,j=1,2…J,Rmj应该指的是第m颗树的某个叶子节点,由上知,当前第m颗树有J个叶子节点.
 C计算每个叶子节点区域Rmj上的输出值(因为样本最终会落在叶子节点上)

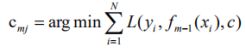
 这个cmj求的应该是当前叶子节点上损失函数的最小值
 上述公式中yi与fm-1(x)用已经算出来的当前提升树残差rmi替换会不会好点?
 其中c指的是初始化决策树f0(x)=c,这个公式的过程就可以理解为在用rmi拟合一颗决策树/回归树的过程
 D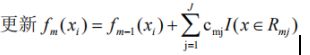

3 得到回归树

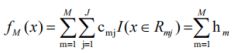
上诉梯度提升算法,在回归问题中,这称之为梯度提升回归树GBRT,在分类问题中(损失函数使用0-1损失等),称之为梯度提升决策树GBDT

4 GBRT的数学实例

帮助对上面内容理解的
训练数据如下表,属性x的取值范围[0.5,10.5],y的取值范围[5.0,10.0]学习GBRT

求解训练数据的切分点s

容易求得在R1,R2内部使得平方损失误差达到最小值的c1,c2为:

求训练数据的切分点,根据所给数据,考虑如下切分点:
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5
对各切分点,不难求出相应的R1,R2,c1,c2及

例如:当s=1.5时,R1={1},R2={2,3…10},c1=5.56,c2=7.50

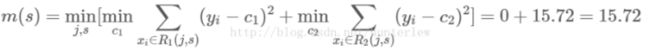
现将s及m(s)的计算结果列表如下:

由上表知,当x=6.5的时候达到最小值,此时R1={1,2…6},R2={7,8,9,10},c1=6.24,c2=8.91,所以回归树T1(x)为:

 所以用的是均值作为预测结果
用f1(x)拟合训练数据的残差见下表,表中r2i=yi-f1(xi),i=1,2…10 ,r2=∑r2i,表示为第二颗决策树要拟合的残差.

第二步求T2(x)方法与T1(x)一样,只是拟合的数据是上表的残差,可以得到:

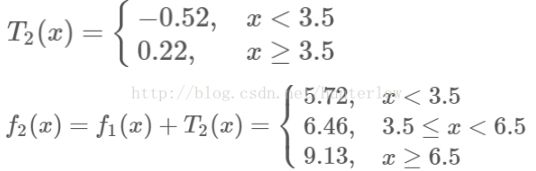
继续求得:


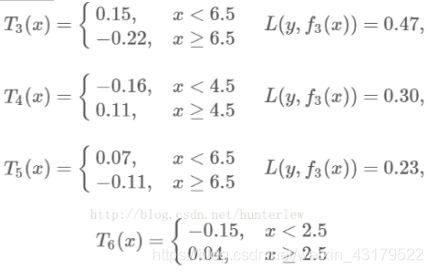
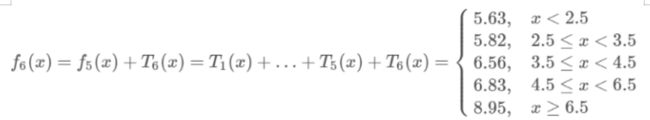
可以用拟合训练数据的平方损失等来作为结束条件.此时

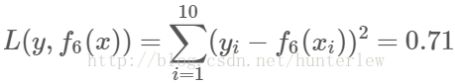
假设此时已经满足误差要求,那么f(x)=f6(x)即为所求回归树

5 API详解

sklearn.ensembleGradientBoostingClassifier
Parameter:
 loss:”deviance”,”exponential” 使用的损失函数 默认值:exponential
 “deviance”:”偏差”
 exponential:指数损失

learning_rate:float类型, 默认值=0.1
 学习率:用于减少每一步的步长,防止步长过长跨过极值点.通常学习率值比较小.但学习率设置的小,需要的决策树数量就比较多,反之也成立
n_estimators:int类型, 默认值=100
 决策树数量(决策树分类器个数)

补充集成学习的多样性增强

1.数据样本扰动
 如Bagging框架中就是利用Boostrap抽样完成对数据样本的自助采样.
2.输入属性扰动
 Bagging框架中的RandomForest的特征抽样
3.算法参数的扰动
 在使用交叉验证(GridSearch网格搜索)来确定机器学习参数时.

总结:集成学习中各个算法分别如何做分类和回归的

1.决策树
 分类:指数损失
 回归:平方损失
2.随机森林
 分类:简单的投票
 回归:简单的平均法
3.AdaBoost
 分类:sgn函数,只能求解二分类问题
 回归:加法
4.GBDT/GBRT
 分类:指数损失
 回归:平方损失