机器视觉——相机标定
1 机器视觉为什么要做相机标定
机器视觉是采用相机成像来实现对三维场景的测量、定位、重建等过程。是一个利用二维图像进行三维反推的过程,我们所处的世界是三维的,而图像或者照片是二维的,可以把相机认为是一个函数,输入量是一个三维场景,输出量是一幅二维图像。正常来说,这个从三维到二维的过程是不可逆的。
如果我们能够找到一个合适的数学模型,来近似以上这个三维到二维的过程,然后找到这个数学模型的反函数,就可以实现二维到三维的的反过程,即:用简单的数学模型来表达复杂的成像过程,并且求出成像的反过程。
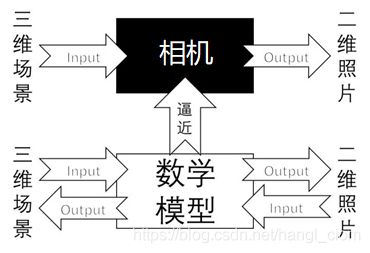
在前几篇文章《机器视觉模型——投影矩阵》以及《机器视觉模型——畸变模型》中,我们讨论了机器视觉的两个重要数学模型——投影成像模型和畸变模型,我们知道,这几个模型中都包含了若干个未知参数。那么这些未知参数如何获得?这就是相机标定的作用了。
2 相机标定的作用
如前所述,成像矩阵及畸变模型中包含了以下几个未知数:
- 内参矩阵:4个参数, f / d x f/dx f/dx、 f / d y f/dy f/dy、 u 0 u_0 u0、 v 0 v_0 v0;
- 外参矩阵:6个参数,相机刚体的位姿,平移和旋转各3个参数。
- 畸变参数:5个参数,径向畸变3个 k 1 k_1 k1、 k 2 k_2 k2、 k 3 k_3 k3,切向畸变2个 p 1 p_1 p1、 p 2 p_2 p2;
相机标定:就是确定相机的内外参数、畸变参数的过程。
相机标定可以说是计算机视觉/机器视觉的基础,任务就是通过具有对应关系的像点和物点的点对,来解出模型的9个(内参+畸变)或15个(内参+畸变+外参)未知参数。 大多数相机标定都是为了标定出相机内参和畸变参数,因为外参属于相机位姿,工作过程中相机位姿是不断变化的,但有些应用,也需要同时标定出外参,即相机位姿。
3 相机标定常用方法
根据标定过程的数学模型,相机标定可以分为:
(1) 线性标定法:运算速度快,标定精度相对不高
(2) 非线性优化标定法:标定精度高,模型复杂,计算量大;
(3) 两步法:以上两者的结合,综合了两者的优缺点,如Tsai两步法、张氏标定法等。
下表给出了几类常用标定方法的对比。
| 标定方法 | 优点 | 缺点 | 常见方法 |
|---|---|---|---|
| 相机自标定法 | 灵活性强、可在线标定 | 精度低、鲁棒性差 | 分层逐步标定、基于Kruppa方程 |
| 主动视觉相机标定法 | 不需要标定物、算法简单、鲁棒性高 | 成本高、设备昂贵 | 主动系统控制相机做特定运动 |
| 标定物标定法 | 可使用于任意的相机模型、 精度高 | 需要标定物、算法复杂 | Tsai两步法、张氏标定法 |
3.1 相机自标定法
相机自标定方法并不需要知道图像点的三维坐标,它通过计算某一点在不同拍摄角度的场景图中的相对关系来确定相机标定的参数问题。自标定法的这种特性,使得它能够完成一些未知相机参数的标定。摄像机自标定方法仅仅利用图像点之间的对应关系或约束关系而不需要标定物就可以得出标定系统的内外参数,这就使得在一些相机任意运动或者复杂未知场景下的相机标定成为现实,这得益于20世纪90年代初,Luong, Faugeras, Maybank等首先提出的自标定概念。
目前,自标定的主要方法有:基于Kruppa方程的自标定法、分层逐步标定法。这些相机自标定方法都是通过相机内参数的约束关系来求解参数,完全忽略相机系统外部的环境,所以这种标定方法比其他方法更灵活,但是稳定性不高。
1) 分层逐步标定法
分层逐步标定法是先对图像的序列做射影重建,在重建的基础上进行放射标定和欧式标定,通过非线性优化算法求得相机内外参数。由于初始参数是模糊值,优化算法收敛性不确定。
2) 基于Kruppa的自标定法
基于Kruppa的自标定法是通过二次曲线建立关于相机内参矩阵的约束方程,至少使用3对图像来标定相机。图像序列长度会影响标定算法的稳定性,无法保证射影空间中的无穷远平面。
3.2 基于主动视觉的标定方法
基于主动视觉的相机标定法是通过主动系统控制相机做特定运动,拍摄多组图像,依据图像信息和已知位移变化来求解相机内外参数。有两种典型的方法:一是使相机在三维空间稳定平移;二是使相机做参数固定的旋转运动。基于主动视觉的标定方法可以简化计算过程,并得到线性结果。这种方法的缺点是需要配备精准的控制平台、系统的成本高、而且对一些运动参数未知的场合和不能控制的场合不适用。
3.3 基于标定物的标定方法
区别于主动视觉标定法,在基于标定物的相机标定中标定物必不可少。它不仅需要明确大小、形状,还要确定物体表面的特殊点坐标。其原理就在于利用数学方法找出某一点的空间坐标和图像坐标的对应关系,进而求取相机参数。典型的有:直接线性变换法(DLT)、Tsai两步法、张正友平面标定法等。其中,标定物又分为立体标定物和平面标定物。立体标定物标定方法操作简便,精度可靠。但是立体标定物制作成本昂贵,加工和维护比较困难,平面标定物制作简单,通过改进的算法也可以保证所需的精度,所以近年来的一些标定方法都是基于平面标定的基础来发展改进的。基于标定物的相机标定法的标定精度对标定物有很高的要求,并且一些工作场合不适合其放置,这些情况也限制了应用范围。
1) Tsai两步法
Tsai两步法是先线性求得相机参数,之后考虑畸变因素,得到初始的参数值,通过非线性优化得到最终的相机参数。Tsai两步法速度较快,但仅考虑径向畸变,当相机畸变严重时,该方法不适用。
2) 张氏标定法
见下节。
4 张氏标定法简介
“张氏标定法”是张正友博士1999年发表在国际顶级会议ICCV上的论文《Flexible Camera Calibration By Viewing a Plane From Unknown Orientations》(文章PDF下载)中,提出的一种利用平面棋盘格进行相机标定的实用方法。
4.1 原理
张氏标定法的基本原理:使用二维方格组成的标定板进行标定,采集标定板不同位姿图片,提取图片中角点像素坐标,通过单应矩阵计算出相机的内外参数初始值,利用非线性最小二乘法估计畸变系数,最后使用极大似然估计法优化参数。
该方法介于摄影标定法和自标定法之间,既克服了摄影标定法需要的高精度三维标定物的缺点,又解决了自标定法鲁棒性差的难题。标定过程仅需使用一个打印出来的棋盘格,并从不同方向拍摄几组图片即可,任何人都可以自己制作标定图案,不仅实用灵活方便,而且精度很高,鲁棒性好。因此很快被全世界广泛采用,极大的促进了三维计算机视觉从实验室走向真实世界的进程。


4.2 标定板
张氏标定法中的一个重要部件是标定板,在标定板上,印刷了拓扑结构,广泛应用的是棋盘格和圆点格,为什么常用棋盘格或原点格?这是因为:棋盘格或原点格的拓扑结构明确且均匀,且检测其拓扑结构的图像处理算法简单且有效。

除了这两类常用图案,标定板格式很多,各标定软件都有对应的标定板格式,但不管什么样式的标定板,其基本作用都是类似的:
- 确定物点和像点的对应性;
- 把标定板中的角点变换到相机坐标系下的坐标,这是因为标定板中的每个角点,在标定板坐标系下的位置是确定并且是已知的。
5 如何完成相机标定
以上论述了相机标定的一些基本知识,那么如果我们要实际标定,应该怎么做?是不是必须读透张正友论文,然后一步一步实现?
5.1 使用成型工具
很多商用软件或工具,已经集成了相机标定功能,比如以下两种典型软件:
5.1.1 Halcon
Halcon软件中的标定助手可完成相机标定,如下图所示为Halcon标定板格式。
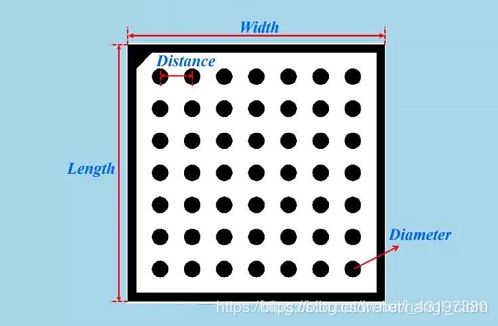
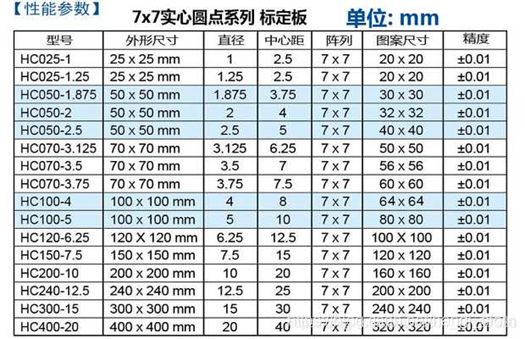
利用Halcon标定助手,按照步骤完成后,即可得到如图的相机内参、外参等标定结果。

5.1.2 Matlab
Matlab中也集成了相机标定工具
其中,Camera Calibrator用于单目相机标定,Stereo Camera Calibrator用于双目相机标定。

标定结果显示:

5.2 编程实现
5.2.1 使用Opencv编程实现
OpenCV中集成了棋盘格角点检测、单应矩阵、内外参解算等相关的函数功能,可利用来构建自己的相机标定工具,这里给出一些常用函数的参考
findChessboardCorners();//棋盘格角点检测
drawChessboardCorners();//棋盘格角点绘制
find4QuadCornerSubpix();//粗提取角点精确化
findHomography();//获取单应矩阵
cornerSubPix();//亚像素检测
calibratCamera();//求解相机内外参
initUndistortRectifyMap();//计算畸变参数
5.2.3 完全自己编程实现
以上各种工具和编程接口,各自有优缺点,实际上每种方法标定的结果都或多或少有一些偏差,精度也不尽相同。
因此,明白了相机标定的原理,在必要的情况下,完全可以自己编程实现,当然这种方法难度也最大,且相机标定的结果(精度、速度等)完全取决于你的程序的性能,但这种方法可根据自己的需要来进行优化和调整,适应性更好。
参考
实战 | 相机标定
http://www.imrobotic.com/news/detail/5302