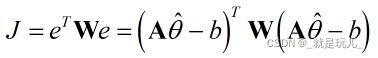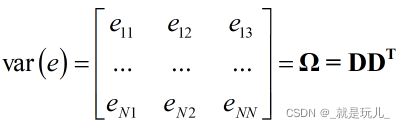最小二乘估计 Least Squares estimation

本文主要讲标准最小二乘方法及其常见的变形：加权最小二乘和总体最小二乘算法，关注不同方法之间的逻辑。

一、最小二乘估计（Least Squares estimation，LS）

最小二乘估计方法是一种不需要先验知识的常见参数估计方法。

假设信号模型为：

在雷达信号中，A为方向矢量，b为阵列接收信号，θ为原始目标信号，n为噪声。更一般的A为观测的系数矩阵，b为观测向量。

A常见有三种情况

1.当A为未知参数等于方程数，则上述方程为适定方程，存在唯一解

2.当A为未知参数小于方程数（行数多于列数），则上述方程为超定方程

3.当A为未知参数大于方程数（行数小于列数），则上述方程为欠收方程

一般雷达系统中最常见的为超定方程，为接收阵列数大于目标数。

最小二乘估计参数的代价函数，该准则为使误差的平方和最小

 代价函数J对未知变量θ求导，令求导结果为0，得到最小二乘的估计为

如果矩阵A是秩亏时，则称该参数是不可辨识的。

但是当误差向量的各个分量具有不同方差，或者各个分量是不相关的，则标准的最小二乘估计不再是最优的，引出需要寻找更一般的方法。

Gauss-Markov定理：

该定理表示超定方程下，如果误差的向量的均值为零矩阵，方差矩阵为

 则该回归方程的最佳线性无偏估计的标准的最小二乘估计。因此当误差向量不满足该定理下的假设时，需要变换到该假设下，进而能得到最佳的估计值。

二、加权最小二乘（Weighted Least Squares estimation，WLS）

当误差向量的方差为为以下的构造形式

 对角线上方差值各不相同，但是对角线外元素为0，不满足Gauss-Markov假设，因此构造一个加权的代价函数，加权误差平方和，来作为优化的目标函数

  再令代价函数最小，对位置参数θ的估计值求导，可得加权最小二乘估计值为

  但是问题是，如何确定加权矩阵。根据误差向量的特定形式且

 矩阵V满足正定矩阵的结构，现代信号处理第三版_张贤达在p43式(2.6.8)有解释新的观测模型的误差向量的方差矩阵为单位矩阵和一常数的乘积，因此满足Gauss-Markov的假设。所以加权最小二乘估计的权值由误差的方差确定

 对加权最小二乘估计的物理解释为，由于噪声的协方差的对角元素值各不相同，根据各自的数值赋予该接收信号权值。如某个元素噪声过大，则与其对应的阵列接收信号向量则受噪声污染更严重，赋予其更小的权值，更愿意相信被噪声污染不严重的接收信号向量。

 三、广义最小二乘（Generalized Least Squares estimation）

 LS估计和WLS估计都是GLS估计的一种特殊形式，当噪声方差矩阵主对角上各元素不相等，同时非对角线上还有非零数值时，即

 LS和WLS的估计值都非最优的，根据噪声方差矩阵的形式构造一个新的模型

 接着对构造的新模型做LS估计得到最优估计结果

 四、总体最小二乘（Total Least Squares estimation）

 实际情况中，除了噪声的扰动导致接收信号有误差之外，系数矩阵A也会含有误差，此时应该同时考虑到接收信号b和系数矩    阵A二者的误差或者扰动，即新的信号模型修改为

 TLS估计的思想是使来自A和b的噪声扰动影响最小，根据信号模型，构造新的等式

 令扰动矩阵D的Frobenious范数最小，其中扰动矩阵

 求该优化方程的方法用到了奇异值分解做最佳逼近；大致过程为求增广矩阵B的奇异值分解，确定B的秩，利用奇异值分解的结果构造逼近矩阵B的估计。接着构造一个逼近矩阵的某些向量构造相关矩阵S，TLS的估计值为S矩阵的逆的归一化数值。具体过程在现代信号处理p133中。有机会详细说一下该过程的核心思想。

五、自适应最小二乘（Recursive Least Squares estimation）

这里是最小二乘的自适应实现，考虑了一种指数加权的最小二乘方法，代价函数为指数加权的误差平方和

有机会详细讲迭代自适应方法及一些典型的应用。

---

其他：

矩阵求逆引理

矩阵求逆引理(matrix inversion lemma)_家家的专栏-CSDN博客_矩阵反转引理

 MATLAB

“Line Fitting with Online Recursive Least Squares Estimation” 是MATLAB给出的一个迭代最小二乘参数估计的例子。

贴出来部分结果，感兴趣可以自行查看matlab相关文档

用来估计的offset和slope参数来做直线拟合。