【数学建模笔记 12】数学建模的回归分析
12. 回归分析
定义
回归分析是对拟合问题作统计分析,包括模型建立、可信度检验、预测和控制。
回归分析的主要步骤是:
- 由观测值确定参数 (回归系数) 的估计值;
- 对线性关系、自变量的显著性进行统计检验;
- 利用回归方程进行预测。
多元线性回归分析
参数估计
对于 m m m 元线性回归模型
y = β 0 + β 1 x 1 + ⋯ + β m x m + ϵ , y=\beta_0+\beta_1x_1+\dots+\beta_mx_m+\epsilon, y=β0+β1x1+⋯+βmxm+ϵ,
对 y y y 作 n n n 次抽样得到 n n n 组数据 ( y i , x i 1 , … , x i m ) , i = 1 , … , n , n > m (y_i,x_{i1},\dots,x_{im}),i=1,\dots,n,n>m (yi,xi1,…,xim),i=1,…,n,n>m,
记
X = ( 1 x 11 … x 1 m 1 x 21 … x 2 m ⋮ ⋮ ⋱ ⋮ 1 x n 1 … x n m ) , Y = ( y 1 y 2 ⋮ y n . ) , X=\begin{pmatrix} 1&x_{11}&\dots&x_{1m}\\ 1&x_{21}&\dots&x_{2m}\\ \vdots&\vdots&\ddots&\vdots\\ 1&x_{n1}&\dots&x_{nm}\\ \end{pmatrix}, Y=\begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_n. \end{pmatrix}, X=⎝⎜⎜⎜⎛11⋮1x11x21⋮xn1……⋱…x1mx2m⋮xnm⎠⎟⎟⎟⎞,Y=⎝⎜⎜⎜⎛y1y2⋮yn.⎠⎟⎟⎟⎞,
ϵ = ( ϵ 1 , ϵ 2 , … , ϵ n ) T , β = ( β 0 , β 1 , … , β m ) T . \epsilon=(\epsilon_1,\epsilon_2,\dots,\epsilon_n)^T,\beta=(\beta_0,\beta_1,\dots,\beta_m)^T. ϵ=(ϵ1,ϵ2,…,ϵn)T,β=(β0,β1,…,βm)T.
于是模型可以表示为
{ Y = X β + ϵ , ϵ ∼ N ( 0 , σ 2 E n ) . \left\{\begin{aligned} &Y=X\beta+\epsilon,\\ &\epsilon\sim N(0,\sigma^2E_n). \end{aligned}\right. {Y=Xβ+ϵ,ϵ∼N(0,σ2En).
选取估计值 b j b_j bj,使当 β j = b j , j = 0 , 1 , … , m \beta_j=b_j,j=0,1,\dots,m βj=bj,j=0,1,…,m 时,误差平方和
Q = ∑ i = 1 n ϵ i 2 = ∑ i = 1 n ( y i − β 0 − β 1 x i 1 − ⋯ − β m x i m ) 2 Q=\sum_{i=1}^n\epsilon_i^2=\sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\dots-\beta_mx_{im})^2 Q=i=1∑nϵi2=i=1∑n(yi−β0−β1xi1−⋯−βmxim)2
最小,为此,令
∂ Q ∂ β j = 0 , j = 0 , 1 , … , m , \frac{\partial Q}{\partial\beta_j}=0,j=0,1,\dots,m, ∂βj∂Q=0,j=0,1,…,m,
得
{ ∑ i = 1 n ( y i − β 0 − β 1 x i 1 − ⋯ − β m x i m ) = 0 , ∑ i = 1 n ( y i − β 0 − β 1 x i 1 − ⋯ − β m x i m ) x i j = 0 , j = 1 , … , m . \left\{\begin{aligned} &\sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\dots-\beta_mx_{im})=0,\\ &\sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\dots-\beta_mx_{im})x_{ij}=0,j=1,\dots,m. \end{aligned}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧i=1∑n(yi−β0−β1xi1−⋯−βmxim)=0,i=1∑n(yi−β0−β1xi1−⋯−βmxim)xij=0,j=1,…,m.
可以化为
X T X β = X T Y , X^TX\beta=X^TY, XTXβ=XTY,
有解
β ^ = ( X T X ) − 1 X T Y . \hat{\beta}=(X^TX)^{-1}X^TY. β^=(XTX)−1XTY.
将 b e t a ^ = ( b 0 , b 1 , … , b m ) \hat{beta}=(b_0,b_1,\dots,b_m) beta^=(b0,b1,…,bm) 代入得
y ^ = b 0 + b 1 x 1 + ⋯ + b m x m , \hat{y}=b_0+b_1x_1+\dots+b_mx_m, y^=b0+b1x1+⋯+bmxm,
于是有残差平方和
S S E = ∑ i = 1 n e i 2 = ∑ i = 1 n ( y i − y i ^ ) 2 . SSE=\sum_{i=1}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2. SSE=i=1∑nei2=i=1∑n(yi−yi^)2.
系数检验
总平方和
S S T = ∑ i = 1 n ( y i − y ‾ ) 2 = S S E + S S R . SST=\sum_{i=1}^n(y_i-\overline{y})^2=SSE+SSR. SST=i=1∑n(yi−y)2=SSE+SSR.
其中 S S R = ∑ i = 1 n ( y i ^ − y ) 2 SSR=\sum_{i=1}^n(\hat{y_i}-y)^2 SSR=∑i=1n(yi^−y)2 称回归平方和。
为检验 y y y 和变量 x 1 , x 2 , … , x m x_1,x_2,\dots,x_m x1,x2,…,xm 是否都有线性关系,假定 y y y 与 x 1 , x 2 , … , x m x_1,x_2,\dots,x_m x1,x2,…,xm 的线性关系都不显著,则所有的 ∣ β j ^ ∣ , j = 1 , … , m |\hat{\beta_j}|,j=1,\dots,m ∣βj^∣,j=1,…,m 都很小。
因此,令原假设为
H 0 : β 1 = β 2 = ⋯ = β m = 0. H_0:\beta_1=\beta_2=\dots=\beta_m=0. H0:β1=β2=⋯=βm=0.
经数学证明,当 H 0 H_0 H0 成立时,满足
F = S S R / m S S E / ( n − m − 1 ) ∼ F ( m , n − m − 1 ) . F=\frac{SSR/m}{SSE/(n-m-1)}\sim F(m,n-m-1). F=SSE/(n−m−1)SSR/m∼F(m,n−m−1).
对显著性水平 α \alpha α,若 F > F α ( m , n − m − 1 ) F>F_\alpha(m,n-m-1) F>Fα(m,n−m−1),回归方程效果显著;反之不显著。
当 H 0 H_0 H0 被拒绝时, β j \beta_j βj 不全为 0,但是不排除其中若干个为 0,应进一步作检验,分别令原假设为
H 0 ( j ) : β j = 0 , j = 0 , 1 , … , m . H_0^{(j)}:\beta_j=0,j=0,1,\dots,m. H0(j):βj=0,j=0,1,…,m.
当 H 0 ( j ) H_0^{(j)} H0(j) 为真时,有
t j = b j / c j j S S E / ( n − m − 1 ) ∼ t ( n − m − 1 ) , t_j=\frac{b_j/\sqrt{c_{jj}}}{\sqrt{SSE/(n-m-1)}}\sim t(n-m-1), tj=SSE/(n−m−1)bj/cjj∼t(n−m−1),
其中 c j j c_{jj} cjj 是 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1 中的第 ( j , j ) (j,j) (j,j) 个元素。
对于 α \alpha α,若 ∣ t j ∣ > t α / 2 ( n − m − 1 ) , j = 1 , 2 , … , m |t_j|>t_{\alpha/2}(n-m-1),j=1,2,\dots,m ∣tj∣>tα/2(n−m−1),j=1,2,…,m, x j x_j xj 显著;否则,去掉变量 x j x_j xj 重新建立回归方程。
还有其他衡量相关成都的指标如
R 2 = S S R S S T . R^2=\frac{SSR}{SST}. R2=SSTSSR.
R = R 2 R=\sqrt{R^2} R=R2 称复相关系数, R R R 越大,相关关系或密切,通常 R > 0.8 或 0.9 R>0.8\ \text{或}\ 0.9 R>0.8 或 0.9 才认为相关。
回归预测
对于给定 x 1 ( 0 ) , … , x m 0 x_1^{(0)},\dots,x_m^{{0}} x1(0),…,xm0,代入得
y 0 ^ = b 0 + b 1 x 1 ( 0 ) + ⋯ + b m x m ( 0 ) \hat{y_0}=b_0+b_1x_1^{(0)}+\dots+b_mx_m^{(0)} y0^=b0+b1x1(0)+⋯+bmxm(0)
作为 y y y 的预测值。
也可以进行区间估计,记 s = S S E n − m − 1 s=\sqrt{\frac{SSE}{n-m-1}} s=n−m−1SSE, x 0 = ( 1 , x 1 ( 0 ) , … , x m ( 0 ) ) x_0=(1,x_1^{(0)},\dots,x_m^{(0)}) x0=(1,x1(0),…,xm(0)),则 y 0 y_0 y0 置信度为 1 − α 1-\alpha 1−α 的预测区间为
( y 0 ^ − t 1 − α / 2 ( n − m − 1 ) s 1 + x 0 T ( X T X ) − 1 x 0 , (\hat{y_0}-t_{1-\alpha/2}(n-m-1)s\sqrt{1+x_0^T(X^TX)^{-1}x_0}, (y0^−t1−α/2(n−m−1)s1+x0T(XTX)−1x0,
y 0 ^ + t 1 − α / 2 ( n − m − 1 ) s 1 + x 0 T ( X T X ) − 1 x 0 ) \hat{y_0}+t_{1-\alpha/2}(n-m-1)s\sqrt{1+x_0^T(X^TX)^{-1}x_0}) y0^+t1−α/2(n−m−1)s1+x0T(XTX)−1x0)
n n n 较大时有:
- 95% 预测区间 ( y 0 ^ − 2 s , y 0 ^ + 2 s ) (\hat{y_0}-2s,\hat{y_0}+2s) (y0^−2s,y0^+2s);
- 98% 预测区间 ( y 0 ^ − 3 s , y 0 ^ + 3 s ) (\hat{y_0}-3s,\hat{y_0}+3s) (y0^−3s,y0^+3s)。
线性回归模型正则化
对于多元线性回归,当 X T X X^TX XTX 不是满秩矩阵时存在多个解,常见做法是引入正则化项,通常有岭回归和 LASSO 回归两种方法。
岭回归
如果 X X X 个变量间存在较强相关性 (共线性),会导致 ∣ X ′ X ∣ ≈ 0 |X'X|\approx0 ∣X′X∣≈0,从而引起 ( X ′ X ) − 1 (X'X)^{-1} (X′X)−1 对角线的值很大,导致 β \beta β 变化非常大。
因此引入惩罚函数 ∑ j = 0 m β j 2 \sum_{j=0}^m\beta_j^2 ∑j=0mβj2,使得 β \beta β 尽量小,从而减少共线性的影响,构造新的目标函数
β ^ ( k ) = ∑ i = 1 n ( y i − β 0 − β 1 x i 1 − ⋯ − β m x i m ) 2 + k ∑ j = 0 m β j 2 . \hat{\beta}(k)=\sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\dots-\beta_mx_{im})^2+k\sum_{j=0}^m\beta_j^2. β^(k)=i=1∑n(yi−β0−β1xi1−⋯−βmxim)2+kj=0∑mβj2.
于是有
β ^ ( k ) = ( X T X + k I ) − 1 X T Y . \hat{\beta}(k)=(X^TX+kI)^{-1}X^TY. β^(k)=(XTX+kI)−1XTY.
对 k k k 的选用可以采用:
- 岭迹法:选取使 β ^ ( k ) \hat{\beta}(k) β^(k) 稳定的最小 k k k 值;
- 均方误差法:选取使岭估计均方误差的最小 k k k 值。
LASSO 回归
与岭回归不同,LASSO 回归的惩罚项是 ∑ j = 0 m ∣ β j ∣ \sum_{j=0}^m|\beta_j| ∑j=0m∣βj∣,从而有目标函数
β ^ ( k ) = ∑ i = 1 n ( y i − β 0 − β 1 x i 1 − ⋯ − β m x i m ) 2 + k ∑ j = 0 m ∣ β j ∣ . \hat{\beta}(k)=\sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\dots-\beta_mx_{im})^2+k\sum_{j=0}^m|\beta_j|. β^(k)=i=1∑n(yi−β0−β1xi1−⋯−βmxim)2+kj=0∑m∣βj∣.
于是有
J ( β ) = ∣ ∣ X β − Y ∣ ∣ 2 2 + k ∣ ∣ β ∣ ∣ 1 . J(\beta)=||X\beta-Y||_2^2+k||\beta||_1. J(β)=∣∣Xβ−Y∣∣22+k∣∣β∣∣1.
Logistic 回归
对于多元线性回归模型
f ( x ) = β 0 + β 1 x 1 + ⋯ + β m x m . f(x)=\beta_0+\beta_1x_1+\dots+\beta_mx_m. f(x)=β0+β1x1+⋯+βmxm.
可以使用阶跃函数转化为分类模型
f ( x ) = { 0 , β 0 + β 1 x 1 + ⋯ + β m x m ≤ 0 , 1 , β 0 + β 1 x 1 + ⋯ + β m x m > 0. f(x)=\left\{\begin{aligned} &0,\beta_0+\beta_1x_1+\dots+\beta_mx_m\le0,\\ &1,\beta_0+\beta_1x_1+\dots+\beta_mx_m>0. \end{aligned}\right. f(x)={0,β0+β1x1+⋯+βmxm≤0,1,β0+β1x1+⋯+βmxm>0.
然而阶跃函数不连续、不可导,于是代入 Sigmoid 函数
f β ( x ) = 1 1 + e − ( β 0 + ∑ j = 1 m β j x j ) . f_\beta(x)=\frac{1}{1+e^{-(\beta_0+\sum_{j=1}^m\beta_jx_j)}}. fβ(x)=1+e−(β0+∑j=1mβjxj)1.
于是有
P { y = 1 ∣ x } = f β ( x ) = p , P\{y=1|x\}=f_\beta(x)=p, P{y=1∣x}=fβ(x)=p,
P { y = 0 ∣ x } = 1 − f β ( x ) = 1 − p . P\{y=0|x\}=1-f_\beta(x)=1-p. P{y=0∣x}=1−fβ(x)=1−p.
故
ln p 1 − p = β 0 + ∑ j = 1 m β j x j . \ln\frac{p}{1-p}=\beta_0+\sum_{j=1}^m\beta_jx_j. ln1−pp=β0+j=1∑mβjxj.
参数估计
Logistic 回归由于涉及概率运算,不便用最小二乘法估计参数,因此另辟蹊径,使用最大似然估计法。
对于上面两式,由于 y y y 只取 0 或 1,可以概括为
P { y ∣ x ; β } = P { y = 1 ∣ x } y [ 1 − P { y = 1 ∣ x } ] 1 − y P\{y|x;\beta\}=P\{y=1|x\}^y[1-P\{y=1|x\}]^{1-y} P{y∣x;β}=P{y=1∣x}y[1−P{y=1∣x}]1−y
= ( 1 1 + e − x β ) y ( 1 − 1 1 + e − x β ) 1 − y . =(\frac{1}{1+e^{-x\beta}})^y(1-\frac{1}{1+e^{-x\beta}})^{1-y}. =(1+e−xβ1)y(1−1+e−xβ1)1−y.
得似然函数
L ( β ) = ∏ i = 1 m P { y i ∣ x i ; β } L(\beta)=\prod_{i=1}^mP\{y_i|x_i;\beta\} L(β)=i=1∏mP{yi∣xi;β}
= ∏ i = 1 m [ f β ( x i ) y i ( 1 − f β ( x i ) ) 1 − y i ] =\prod_{i=1}^m[f_\beta(x_i)^{y_i}(1-f_\beta(x_i))^{1-y_i}] =i=1∏m[fβ(xi)yi(1−fβ(xi))1−yi]
为求解方便,取对数得
L ~ ( β ) = ∑ i = 1 n [ y i ln f β ( x i ) + ( 1 − y i ) ln ( 1 − f β ( x i ) ) ] . \widetilde{L}(\beta)=\sum_{i=1}^n[y_i\ln f_\beta(x_i)+(1-y_i)\ln(1-f_\beta(x_i))]. L (β)=i=1∑n[yilnfβ(xi)+(1−yi)ln(1−fβ(xi))].
可以使用梯度下降法上式求最大值,从而得到参数。
Python 代码
多元线性回归分析
对于下例
| x1 | x2 | y |
|---|---|---|
| 7 | 26 | 78.5 |
| 1 | 29 | 74.3 |
| 11 | 56 | 104.3 |
| 11 | 31 | 87.6 |
| 7 | 52 | 95.9 |
| 11 | 55 | 109.2 |
| 3 | 71 | 102.7 |
求线性回归模型 y = β 0 + β 1 x 1 + β 2 x 2 y=\beta_0+\beta_1x_1+\beta_2x_2 y=β0+β1x1+β2x2 的估计值。
sklearn
使用 sklearn 求解,代码如下:
# %%
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
# %%
df = pd.DataFrame({
'x1': [7, 1, 11, 11, 7, 11, 3],
'x2': [26, 29, 56, 31, 52, 55, 71],
'y': [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7],
})
X = np.array(df[['x1','x2']])
y = np.array(df[['y']])
model = LinearRegression().fit(X, y)
# %%
b0 = model.intercept_[0]
b1, b2 = model.coef_[0]
print('y = {:.4f} + {:.4f}*x1 + {:.4f}*x2'.format(b0, b1,b2))
print('R_square =',model.score(X,y))
输出如下:
y = 51.5697 + 1.4974*x1 + 0.6723*x2
R_square = 0.9744954805639265
statsmodels
使用 statsmodels 求解,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-26
# @ function: 使用 statsmodels 进行多元线性回归
# %%
import numpy as np
import pandas as pd
from statsmodels.formula.api import ols
# %%
dic = {
'x1': [7, 1, 11, 11, 7, 11, 3],
'x2': [26, 29, 56, 31, 52, 55, 71],
'y': [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7],
}
model = ols('y~x1+x2', dic).fit()
# %%
model.summary()
输出如下:
| Dep. Variable: | y | R-squared: | 0.974 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.962 |
| Method: | Least Squares | F-statistic: | 76.42 |
| Date: | Mon, 26 Jul 2021 | Prob (F-statistic): | 0.000650 |
| Time: | 21:19:31 | Log-Likelihood: | -14.732 |
| No. Observations: | 7 | AIC: | 35.46 |
| Df Residuals: | 4 | BIC: | 35.30 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 51.5697 | 3.523 | 14.640 | 0.000 | 41.789 | 61.350 |
| x1 | 1.4974 | 0.264 | 5.681 | 0.005 | 0.766 | 2.229 |
| x2 | 0.6723 | 0.063 | 10.717 | 0.000 | 0.498 | 0.847 |
| Omnibus: | nan | Durbin-Watson: | 2.660 |
|---|---|---|---|
| Prob(Omnibus): | nan | Jarque-Bera (JB): | 1.891 |
| Skew: | 1.273 | Prob(JB): | 0.388 |
| Kurtosis: | 2.992 | Cond. No. | 174. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
两者结果相同, β 0 = 51.5697 , β 1 = 1.4974 , β 2 = 0.6723 , R 2 = 0.974 \beta_0=51.5697,\beta_1=1.4974,\beta_2=0.6723,R^2=0.974 β0=51.5697,β1=1.4974,β2=0.6723,R2=0.974,不过 statsmodels 输出了非常详细的报告。
岭回归
对上例进行岭回归,并选择合适的 k k k 值,使用 sklearn 求解,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-26
# @ function: 使用 sklearn 进行岭回归
# %%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, RidgeCV
# %%
# 源数据
df = pd.DataFrame({
'x1': [7, 1, 11, 11, 7, 11, 3],
'x2': [26, 29, 56, 31, 52, 55, 71],
'y': [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7],
})
X = np.array(df[['x1', 'x2']])
y = np.array(df[['y']])
# 遍历 k,计算不同 k 时的拟合结果
k_array = np.logspace(-4, 1.5, 100)
x1_list, x2_list = [], []
for k in k_array:
model = Ridge(alpha=k).fit(X, y)
x1_list.append(model.coef_[0][0])
x2_list.append(model.coef_[0][1])
# %%
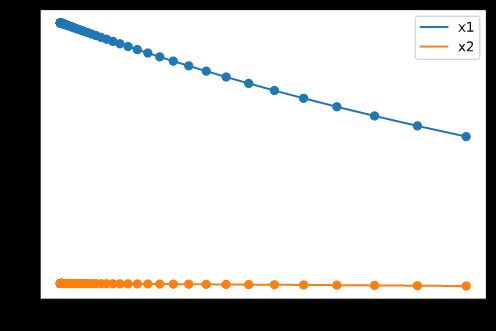
# 作岭迹图
plt.scatter(k_array,x1_list)
plt.scatter(k_array,x2_list)
plt.plot(k_array, x1_list, label='x1')
plt.plot(k_array, x2_list, label='x2')
plt.legend()
# %%
# 自动匹配最佳 k 值
model2 = RidgeCV().fit(X, y)
# %%
# 截距
b0 = model2.intercept_[0]
# 系数
b1, b2 = model2.coef_[0][0], model2.coef_[0][1]
print('y = {:.4f} + {:.4f}*x1 + {:.4f}*x2'.format(b0, b1, b2))
print('R_square =', model2.score(X, y))
print('k =', model2.alpha_)
输出如下:
y = 52.6722 + 1.3610*x1 + 0.6700*x2
R_square = 0.9727637007583043
k = 10.0
上图为 k k k 取不同值时的 x 1 , x 2 x_1,x_2 x1,x2 的系数 β 1 , β 2 \beta_1,\beta_2 β1,β2 的变化,可以看到该问中系数的变化是相对稳定的,没有明显的拐点,这说明变量间不存在显著的共线性。
使用 sklearn 自动匹配最佳 k k k 值,结果为 k k k,并有 y = 52.6722 + 1.3610 x 1 + 0.6700 x 2 y = 52.6722 + 1.3610x_1 + 0.6700x_2 y=52.6722+1.3610x1+0.6700x2,此时 R 2 = 0.9728 R^2=0.9728 R2=0.9728。
LASSO 回归
同样进行 LASSO 回归,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-26
# @ function: 使用 sklearn 进行 lASSO 回归
# %%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso, LassoCV
# %%
# 源数据
df = pd.DataFrame({
'x1': [7, 1, 11, 11, 7, 11, 3],
'x2': [26, 29, 56, 31, 52, 55, 71],
'y': [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7],
})
X = np.array(df[['x1', 'x2']])
y = np.array(df[['y']])
# 遍历 k,计算不同 k 时的拟合结果
k_array = np.logspace(-4, 1.5, 100)
x1_list, x2_list = [], []
for k in k_array:
model = Lasso(alpha=k).fit(X, y)
x1_list.append(model.coef_[0])
x2_list.append(model.coef_[1])
# %%
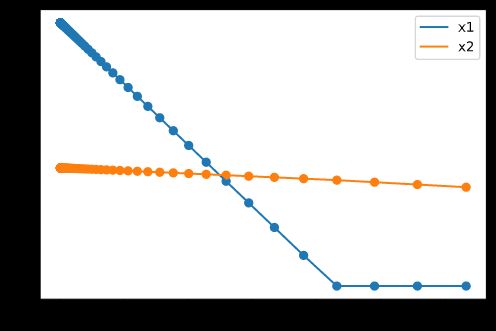
# 作岭迹图
plt.scatter(k_array,x1_list)
plt.scatter(k_array,x2_list)
plt.plot(k_array, x1_list, label='x1')
plt.plot(k_array, x2_list, label='x2')
plt.legend()
# %%
# 自动匹配最佳 k 值
model2 = LassoCV().fit(X, y)
# %%
# 截距
b0 = model2.intercept_
# 系数
b1, b2 = model2.coef_[0], model2.coef_[1]
print('y = {:.4f} + {:.4f}*x1 + {:.4f}*x2'.format(b0, b1, b2))
print('R_square =', model2.score(X, y))
print('k =', model2.alpha_)
输出如下:
y = 52.7036 + 1.3770*x1 + 0.6667*x2
R_square = 0.973087311206934
k = 1.7257551020408168
与岭回归不同的是,LASSO 回归系数变化是平直且突变的。
Logistic 回归
对下例
| 甜度 | 密度 | 体积 | 质量 | 是否为好瓜 |
|---|---|---|---|---|
| 0.95 | 0.876 | 1.85 | 2.51 | 是 |
| 0.76 | 0.978 | 2.14 | 2.45 | 是 |
| 0.82 | 0.691 | 1.34 | 1.34 | 否 |
| 0.57 | 0.745 | 1.38 | 1.15 | 否 |
| 0.69 | 0.512 | 0.67 | 1.23 | 否 |
| 0.77 | 0.856 | 2.35 | 3.95 | 是 |
| 0.89 | 1.297 | 1.69 | 2.67 | 是 |
进行 Logistic 回归分析,并进行预测。
sklearn
使用 sklearn 实现,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-26
# @ function: 使用 sklearn 进行岭回归
# %%
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
# %%
# 源数据
df = pd.DataFrame({
'good': [1, 1, 0, 0, 0, 1, 1],
'sweet': [.95, .76, .82, .57, .69, .77, .89],
'density': [.876, .978, .691, .745, .512, .856, 1.297],
'volume': [1.85, 2.14, 1.34, 1.38, 0.67, 2.35, 1.69],
'quality': [2.51, 2.45, 1.34, 1.15, 1.23, 3.95, 2.67],
})
# 样本集
X = np.array(df[df.columns[1:]])
# 标签集
y = np.array(df['good'])
# 建立模型
model = LogisticRegression()
model.fit(X, y)
# %%
# 截距
b0 = model.intercept_[0]
# 系数
b1, b2, b3, b4 = model.coef_[0][0], model.coef_[0][1], \
model.coef_[0][2], model.coef_[0][3]
b0, b1, b2, b3, b4
# %%
df2 = pd.DataFrame({
'sweet': [.5, 1],
'density': [.5, 1],
'volume': [.5, 2],
'quality': [.5, 2],
})
model.predict(np.array(df2))
输出如下:
# 截距...
(-3.370933696851626,
0.13186817837303025,
0.29709467699778236,
0.6067592080789701,
1.1302193116167027)
array([0, 1], dtype=int64)
前 5 个值代表系数 β 0 = − 3.37 , \beta_0=-3.37, β0=−3.37, β 1 = 0.13 , \beta_1=0.13, β1=0.13, β 2 = 0.30 , \beta_2=0.30, β2=0.30, β 3 = 0.61 , \beta_3=0.61, β3=0.61, β 4 = 1.13 \beta_4=1.13 β4=1.13。
后 2 个值代表对两个样本的预测。第一个样本甜度、密度、体积、质量全为 0.5;第二个样本甜度、密度为 1,体积、质量为 2。预测结果为:
- 第一个样本:不是好瓜;
- 第二个样本:是好瓜。
可以代入验算,对于
p = 1 1 + e − ( β 0 + ∑ i = 1 4 β i x i ) p=\frac{1}{1+e^{-(\beta_0+\sum_{i=1}^4\beta_ix_i)}} p=1+e−(β0+∑i=14βixi)1
当 β 0 = − 3.37 , \beta_0=-3.37, β0=−3.37, β 1 = 0.13 , \beta_1=0.13, β1=0.13, β 2 = 0.30 , \beta_2=0.30, β2=0.30, β 3 = 0.61 , \beta_3=0.61, β3=0.61, β 4 = 1.13 \beta_4=1.13 β4=1.13 时,
当 x 1 = x 2 = x 3 = x 4 = 0.5 x_1=x_2=x_3=x_4=0.5 x1=x2=x3=x4=0.5 时, p = 0.1015 p=0.1015 p=0.1015,不是好瓜的可能性更大。
当 x 1 = x 2 = 1 , x 3 = x 4 = 2 x_1=x_2=1,x_3=x_4=2 x1=x2=1,x3=x4=2 时, p = 0.6299 p=0.6299 p=0.6299,是好瓜的可能性更大。
statsmodels
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-26
# @ function: 使用 sklearn 进行岭回归
# %%
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
# %%
# 源数据
df = pd.DataFrame({
'good': [1, 1, 0, 0, 0, 1, 1],
'sweet': [.95, .76, .82, .57, .69, .77, .89],
'density': [.876, .978, .691, .745, .512, .856, 1.297],
'volume': [1.85, 2.14, 1.34, 1.38, 0.67, 2.35, 1.69],
'quality': [2.51, 2.45, 1.34, 1.15, 1.23, 3.95, 2.67],
})
# 建立模型
model = smf.logit('good~sweet+density+volume+quality', df)
# %%
res = model.fit(method='bfgs')
res.summary()
# %%
df2 = pd.DataFrame({
'good': [None, None],
'sweet': [.5, 1],
'density': [.5, 1],
'volume': [.5, 2],
'quality': [.5, 2],
})
res.predict(df2)
输出结果为:
| Dep. Variable: | good | No. Observations: | 7 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 2 |
| Method: | MLE | Df Model: | 4 |
| Date: | Mon, 26 Jul 2021 | Pseudo R-squ.: | 1.000 |
| Time: | 22:56:51 | Log-Likelihood: | -2.8779e-05 |
| converged: | True | LL-Null: | -4.7804 |
| Covariance Type: | nonrobust | LLR p-value: | 0.04852 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -28.6968 | 2005.820 | -0.014 | 0.989 | -3960.032 | 3902.639 |
| sweet | -13.9757 | 2808.332 | -0.005 | 0.996 | -5518.206 | 5490.254 |
| density | -4.8468 | 2477.251 | -0.002 | 0.998 | -4860.170 | 4850.476 |
| volume | -0.5361 | 1024.433 | -0.001 | 1.000 | -2008.387 | 2007.315 |
| quality | 23.2646 | 1230.217 | 0.019 | 0.985 | -2387.917 | 2434.446 |
0 2.428405e-12
1 1.128262e-01
dtype: float64
有 β 0 = − 28.6968 , β 1 = − 13.9757 , β 2 = − 4.868 , β 3 = − 0.5361 , β 4 = 23.2646 \beta_0=-28.6968,\beta_1=-13.9757,\beta_2=-4.868,\beta_3=-0.5361,\beta_4=23.2646 β0=−28.6968,β1=−13.9757,β2=−4.868,β3=−0.5361,β4=23.2646,预测结果为 p 1 = 0 , p 2 = 0.1128 p_1=0,p_2=0.1128 p1=0,p2=0.1128,不是好瓜的概率都很大。
注意到 statsmodels 的结果与 sklearn 不同,原因是采用了不同的求解方法。