神经网络实现 mnist数据集

• 识别mnist算是神经网络算法的"Hello World!"程序,下面是两种简单的实现方式

环境说明:

Ubuntu20.04
Python3.8
Tensorflow 2.2.0

基于keras库

from keras import models #导入keras的models
from keras import layers #导入layers
from keras.datasets import mnist #导入mnist数据集
from keras.utils import to_categorical #用来将标签由一个数字转换为一个向量

model = models.Sequential() #定义神经网络模型
model.add(layers.Dense(512,activation='relu',input_shape=(28*28,))) #添加一个神经元层,由512个神经元组成,激活函数为'relu',输入大小28*28(每张mnist图片有28*28个像素点)
model.add(layers.Dense(10,activation='softmax')) #添加第二个神经元层,作为输出层,由10个神经元组成,softmax激活函数将其数字转化为一个介于0-1之间的数字,代表属于每一类的概率
model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) #传入模型的损失函数,优化器,训练和测试时使用的指标函数

(train_data,train_label),(test_data,test_lable) = mnist.load_data() #引入minst数据集
#print(train_data.shape) #(60000,28,28),代表60000张图片,每张图片由28*28的灰度值矩阵表示
train_data = train_data.reshape((60000,28*28)) #将表示图片的矩阵转换为向量,便于传给神经网络模型
train_data = train_data.astype('float32')/255 #mnist数据集用0-255表示灰度值,将其转换为0-1之间的数字
test_data = test_data.reshape((10000,28*28)) #转换测试数据集,同训练测试集
test_data = test_data.astype('float32')/255
#print(train_label.shape) #(60000,)
train_label = to_categorical(train_label) #将每个数字转换为一个1*10的向量,方便神经网络处理
test_lable = to_categorical(test_lable)

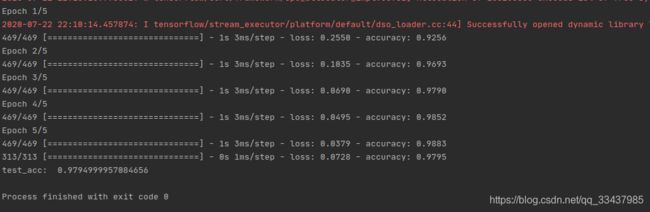
model.fit(train_data,train_label,epochs=5,batch_size=128) #训练模型,训练5轮
test_loss,test_acc = model.evaluate(test_data,test_lable) #在测试数据集上测试模型的准确性
print('test_acc: ',test_acc) #test_acc:  0.9794999957084656,每次结果都不一样

手撕神经网络(无需Tensorflow) 待续未完

• 实现激活函数

#lib.nn_activators
import numpy as np #导入numpy库,numpy是Python进行科学计算时的一个重要基础模块

class ReLUActivator: #定义ReLU类，ReLU全称Revtified Linear Unit(修正线性单元)
    def value(self,s): #计算激活函数值
        return np.maximum(0,s)

    def derivative(self,s): #返回此激活函数的导数值
        return (s>0).astype(np.int)

• 实现Layer 神经元层

#lib.nn_layers
import numpy as np
from lib.nn_activators import ReLUActivator #导入上面的ReLU类

class Layer: #定义神经元层
    def __init__(self,n_input,n_output,activator = ReLUActivator):#类的初始化函数,接受3个参数,输入神经元个数(即上层神经元个数),输出神经元个数(即本层神经元个数),激活函数,默认为ReLU函数
        self.activator = activator #定义类的激活函数为传入的激活函数
        self.b = np.zeros((n_output,1)) #定义偏置向量,大小为(n*1),初始化为全0向量
        r = np.sqrt(6.0/(n_input+n_output)) #计算r
        self.W = np.random.uniform(-r,r,(n_output,n_input)) #将权重矩阵的每一个元素初始化成[-r,r]区间的一个随机数,这样的初始化方法成为Xavier初始化
        self.outputs = np.zeros((n_output,1)) #初始化输出为全0向量

    def forward(self,inputs): #forward函数的功能是对给定的输入,计算层中神经元的输出值
        self.inputs = inputs
        self.sums = self.W.dot(inputs) + self.b #s(r) = W(r)v(r-1) + b(r)
        self.outputs = self.activator.value(self.sums) #v(r) = 本层激活函数(s(r))

    def back_propagation(self,delta_in,learning_rate): #定义反向传播算法,参数为下层反向传播来的delta_in,学习速率
        d = self.activator.derivative(self.sums) * delta_in #d(r)=delta_in * 激活函数的导数(s(r))
        self.delta_out = self.W.T.dot(d) #保存待传给上一层的梯度(即上一层将使用的delta_in)
        self.W_grad = d.dot(self.inputs.T) #计算损失函数对权重矩阵的梯度
        self.b_grad = d #计算损失函数对偏置向量的梯度
        self.W -= learning_rate * self.W_grad #更新权重矩阵
        self.b -= learning_rate * self.b_grad #更新偏置向量

• 为了运行随机梯度下降算法,还需指定损失函数

#lib.nn_loss
import numpy as np

class MSE: #均方误差,回归问题的损失函数
    def value(self,y,v): #计算均方误差值
        return (v-y)**2

    def derivative(self,y,v): #计算均方误差的导数
        return 2*(v-y)

def softmax(v): #softmax函数,将向量里面的值转换到0-1区间,表示属于某类的概率
    e = np.exp(v) #每个值变为自身的e的本身次方 如:原向量[1,2,-2],转换后为[exp(1),exp(2),exp(-2)]
    s = e.sum(axis=0) #计算转换后的和
    for i in range(len(s)): #将向量里面的值转换到0-1区间
        e[i] /= s[i]
    return e #返回转换后的向量

class SoftmaxCrossEntropy: #k元交叉熵,分类问题的损失函数
    def value(self,y,v): #计算k元交叉熵
        p = softmax(v)
        return -(y*np.log(p)).sum()

    def derivative(self,y,v): #计算k元交叉熵的导数
        p = softmax(v)
        return p-y

• 有了神经元层和损失函数之后,就可以构造一个完整的神经网络

#lib.neural_network
import numpy as np

class NeuralNetwork: #定义神经函数类
    def __init__(self,layers,loss): #类的初始化函数,参数为神经元层和损失函数(回归问题传入MSE,分类问题传入SoftmaxCrossEntropy)
        self.layers = layers
        self.loss = loss

    def forward(self,x): #对x计算当前参数所对应的神经网络的最终输出
        layers = self.layers
        inputs = x #神经网络模型的输入
        for layer in layers: #循环模型中的每一个神经元层
            layer.forward(inputs) #计算inputs在该层的输出
            inputs = layer.outputs #将这个神经元层对应的输出作为下一个神经元层的输入
        return inputs #返回最终结果

    def back_propagation(self,y,outputs,learning_rate): #实现反向传播算法
        delta_in = self.loss.derivative(y,outputs)
        for layer in self.layers[::-1]:
            layer.back_propagation(delta_in,learning_rate)
            delta_in = layer.delta_out

    def fit(self,X,y,N,learning_rate):
        for t in range(N):
            i = np.random.randint(0,len(X))
            outputs = self.forward(X[i].reshape(-1,1))
            self.back_propagation(y[i].reshape(-1,1),outputs,learning_rate)

    def predict(self,X):
        y = []
        for i in range(len(X)):
            v = self.forward(X[i].reshape(-1,1).reshape(-1))
            y.append(v)
        return np.array(y)

参考书籍

1. François Chollet《Deep Learning with Python》
2. 王磊《机器学习 算法导论》