深度学习教程 | 神经网络基础
- 作者:韩信子@ShowMeAI
- 教程地址:http://www.showmeai.tech/tutorials/35
- 本文地址:http://www.showmeai.tech/article-detail/213
- 声明:版权所有,转载请联系平台与作者并注明出处
收藏ShowMeAI查看更多精彩内容
本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得,对应的课程视频可以在这里查看。
引言
在ShowMeAI前一篇文章 深度学习概论 中我们对深度学习(Deep Learning)进行了简单介绍:
- 我们以房价预测为例,对应讲解了神经网络(Neural Network)模型结构和基础知识。
- 介绍了针对监督学习的几类典型神经网络:Standard NN,CNN和RNN。
- 介绍了「结构化数据」和「非结构化数据」2种不同类型的数据。
- 分析了近些年来深度学习热门,及其性能优于传统机器学习的原因(Data,Computation和Algorithms)。
本节内容我们展开介绍神经网络的基础:逻辑回归(Logistic Regression)。我们将通过对逻辑回归模型结构的分析,过渡到后续神经网络模型。(关于逻辑回归模型,大家也可以阅读ShowMeAI的文章 图解机器学习 | 逻辑回归算法详解 学习)
1.算法基础与逻辑回归
逻辑回归(Logistic regression) 是一个用于二分类的算法。
1.1 二分类问题与机器学习基础
二分类就是输出 y y y只有 {0,1} 两个离散值(也有 {-1,1} 的情况)。我们以一个「图像识别」问题为例,判断图片是否是猫。识别是否是「猫」,这是一个典型的二分类问题——0代表「非猫(not cat)」,1代表「猫(cat)」。(关于机器学习基础知识大家也可以查看ShowMeAI文章 图解机器学习 | 机器学习基础知识)。
从机器学习的角度看,我们的输入 x x x此时是一张图片,彩色图片包含RGB三个通道,图片尺寸为 ( 64 , 64 , 3 ) (64,64,3) (64,64,3)。
有些神经网络的输入是一维的,我们可以将图片 x x x(维度 ( 64 , 64 , 3 ) (64,64,3) (64,64,3))展平为一维特征向量(feature vector),得到的特征向量维度为 ( 12288 , 1 ) (12288,1) (12288,1)。我们一般用列向量表示样本,把维度记为 n x n_x nx。
如果训练样本有 m m m张图片,那么我们用矩阵存储数据,此时数据维度变为 ( n x , m ) (n_x,m) (nx,m)。
- 矩阵 X X X的行 n x n_x nx代表了每个样本 x ( i ) x^{(i)} x(i)特征个数
- 矩阵 X X X的列 m m m代表了样本个数。
我们可以对训练样本的标签 Y Y Y也做一个规整化,调整为1维的形态,标签 Y Y Y的维度为 ( 1 , m ) (1,m) (1,m)。
1.2 逻辑回归算法
逻辑回归是最常见的二分类算法(详细算法讲解也可阅读ShowMeAI文章 图解机器学习 | 逻辑回归算法详解),它包含以下参数:
- 输入的特征向量: x ∈ R n x x \in R^{n_x} x∈Rnx,其中 n x {n_x} nx是特征数量
- 用于训练的标签: y ∈ 0 , 1 y \in 0,1 y∈0,1
- 权重: w ∈ R n x w \in R^{n_x} w∈Rnx
- 偏置: b ∈ R b \in R b∈R
- 输出: y ^ = σ ( w T x + b ) \hat{y} = \sigma(w^Tx+b) y^=σ(wTx+b)
输出计算用到了Sigmoid函数,它是一种非线性的S型函数,输出被限定在 [ 0 , 1 ] [0,1] [0,1] 之间,通常被用在神经网络中当作激活函数(Activation Function)使用。
Sigmoid函数的表达式如下:
s = σ ( w T x + b ) = σ ( z ) = 1 1 + e − z s = \sigma(w^Tx+b) = \sigma(z) = \frac{1}{1+e^{-z}} s=σ(wTx+b)=σ(z)=1+e−z1
实际上,逻辑回归可以看作非常小的一个神经网络。
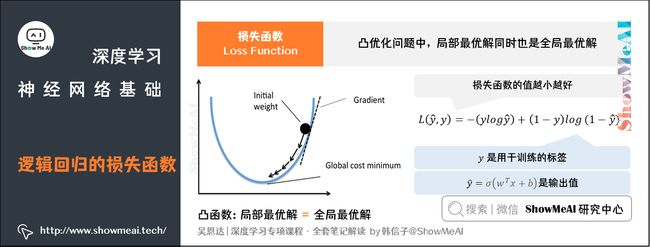
1.3 逻辑回归的损失函数
在机器学习中,**损失函数(loss function)**用于量化衡量预测结果与真实值之间的差距,我们会通过优化损失函数来不断调整模型权重,使其最好地拟合样本数据。
在回归类问题中,我们会使用均方差损失(MSE):
L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\hat{y},y) = \frac{1}{2}(\hat{y}-y)^2 L(y^,y)=21(y^−y)2
但是在逻辑回归中,我们并不倾向于使用这样的损失函数。逻辑回归使用平方差损失会得到非凸的损失函数,它会有很多个局部最优解。梯度下降法可能找不到全局最优值,从而给优化带来困难。
因此我们调整成使用对数损失(二元交叉熵损失):
L ( y ^ , y ) = − ( y log y ^ ) + ( 1 − y ) log ( 1 − y ^ ) L(\hat{y},y) = -(y\log\hat{y})+(1-y)\log(1-\hat{y}) L(y^,y)=−(ylogy^)+(1−y)log(1−y^)
刚才我们给到的是单个训练样本中定义的损失函数,它衡量了在单个训练样本上的表现。我们定义代价函数(Cost Function,或者称作成本函数)为全体训练样本上的表现,即 m m m个样本的损失函数的平均值,反映了 m m m个样本的预测输出与真实样本输出 y y y的平均接近程度。
成本函数的计算公式如下:
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i))
2.梯度下降法(Gradient Descent)
刚才我们了解了损失函数(Loss Function)与成本函数定义,下一步我们就要找到最优的 w w w和 b b b值,最小化 m m m个训练样本的Cost Function。这里用到的方法就叫做梯度下降(Gradient Descent)算法。
在数学上,1个函数的梯度(gradient)指出了它的最陡增长方向。也就是说,沿着梯度的方向走,函数增长得就最快。那么沿着梯度的负方向走,函数值就下降得最快。
(更详细的最优化数学知识可以阅读ShowMeAI文章 图解AI数学基础 | 微积分与最优化)
模型的训练目标是寻找合适的 w w w与 b b b以最小化代价函数值。我们先假设 w w w与 b b b都是一维实数,则代价函数 J J J关于 w w w与 b b b的图如下所示:
上图中的代价函数 J J J是一个凸函数,只有一个全局最低点,它能保证无论我们初始化模型参数如何(在曲面上任何位置),都能够寻找到合适的最优解。
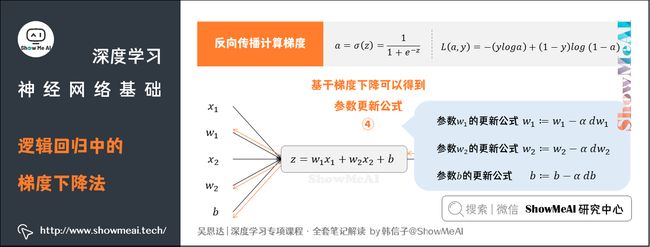
基于梯度下降算法,得到以下参数 w w w的更新公式:
w : = w − α d J ( w , b ) d w w := w - \alpha\frac{dJ(w, b)}{dw} w:=w−αdwdJ(w,b)
公式中 α \alpha α为学习率,即每次更新的 w w w的步长。
成本函数 J ( w , b ) J(w, b) J(w,b)中对应的参数 b b b更新公式为:
b : = b − α d J ( w , b ) d b b := b - \alpha\frac{dJ(w, b)}{db} b:=b−αdbdJ(w,b)
3.计算图(Computation Graph)
对于神经网络而言,训练过程包含了两个阶段:前向传播(Forward Propagation)和反向传播(Back Propagation)。
- 前向传播是从输入到输出,由神经网络前推计算得到预测输出的过程
- 反向传播是从输出到输入,基于Cost Function对参数 w w w和 b b b计算梯度的过程。
下面,我们结合一个例子用计算图(Computation graph)的形式来理解这两个阶段。
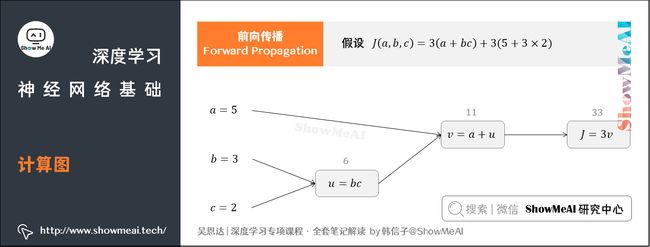
3.1 前向传播(Forward Propagation)
假如我们的Cost Function为 J ( a , b , c ) = 3 ( a + b c ) J(a,b,c)=3(a+bc) J(a,b,c)=3(a+bc),包含 a a a、 b b b、 c c c三个变量。
我们添加一些中间变量,用 u u u表示 b c bc bc, v v v表示 a + u a+u a+u,则 J = 3 v J=3v J=3v。
整个过程可以用计算图表示:
在上图中,我们让 a = 5 a=5 a=5, b = 3 b=3 b=3, c = 2 c=2 c=2,则 u = b c = 6 u=bc=6 u=bc=6, v = a + u = 11 v=a+u=11 v=a+u=11, J = 3 v = 33 J=3v=33 J=3v=33。
计算图中,这种从左到右,从输入到输出的过程,就对应着神经网络基于 x x x和 w w w计算得到Cost Function的前向计算过程。
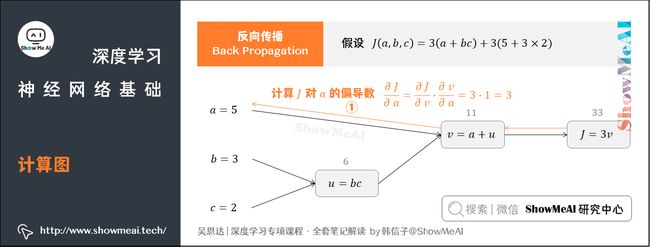
3.2 反向传播(Back Propagation)
我们接着上个例子中的计算图讲解反向传播,我们的输入参数有 a a a、 b b b、 c c c三个。
① 先计算 J J J对参数 a a a的偏导数
从计算图上来看,从右到左, J J J是 v v v的函数, v v v是 a a a的函数。基于求导链式法则得到:
∂ J ∂ a = ∂ J ∂ v ⋅ ∂ v ∂ a = 3 ⋅ 1 = 3 \frac{\partial J}{\partial a}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial a}=3\cdot 1=3 ∂a∂J=∂v∂J⋅∂a∂v=3⋅1=3
② 计算 J J J对参数 b b b的偏导数
从计算图上来看,从右到左, J J J是 v v v的函数, v v v是 u u u的函数, u u u是 b b b的函数。同样可得:
∂ J ∂ b = ∂ J ∂ v ⋅ ∂ v ∂ u ⋅ ∂ u ∂ b = 3 ⋅ 1 ⋅ c = 3 ⋅ 1 ⋅ 2 = 6 \frac{\partial J}{\partial b}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial u}\cdot \frac{\partial u}{\partial b}=3\cdot 1\cdot c=3\cdot 1\cdot 2=6 ∂b∂J=∂v∂J⋅∂u∂v⋅∂b∂u=3⋅1⋅c=3⋅1⋅2=6
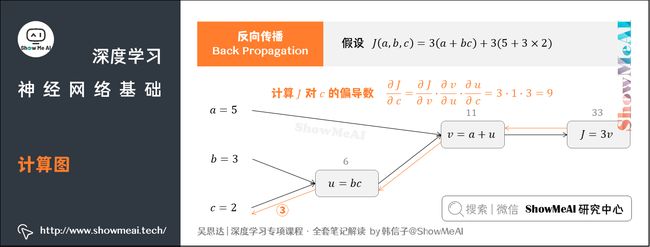
③ 计算 J J J对参数 c c c的偏导数
此时从右到左, J J J是 v v v的函数, v v v是 u u u的函数, u u u是 c c c的函数。可得:
∂ J ∂ c = ∂ J ∂ v ⋅ ∂ v ∂ u ⋅ ∂ u ∂ c = 3 ⋅ 1 ⋅ b = 3 ⋅ 1 ⋅ 3 = 9 \frac{\partial J}{\partial c}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial u}\cdot \frac{\partial u}{\partial c}=3\cdot 1\cdot b=3\cdot 1\cdot 3=9 ∂c∂J=∂v∂J⋅∂u∂v⋅∂c∂u=3⋅1⋅b=3⋅1⋅3=9
这样就完成了从右往左的反向传播与梯度(偏导)计算过程。
4.逻辑回归中的梯度下降法
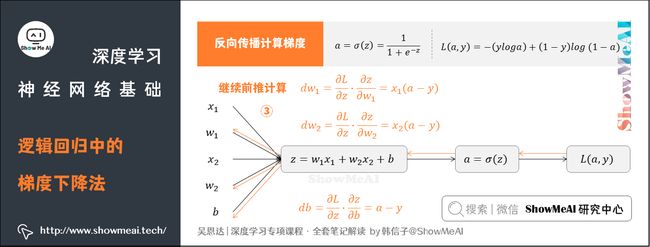
回到我们前面提到的逻辑回归问题,我们假设输入的特征向量维度为2(即 [ x 1 , x 2 ] [x_1, x_2] [x1,x2]),对应权重参数 w 1 w_1 w1、 w 2 w_2 w2、 b b b得到如下的计算图:
反向传播计算梯度
① 求出 L L L对于 a a a的导数
② 求出 L L L对于 z z z的导数
③ 继续前推计算
④ 基于梯度下降可以得到参数更新公式
前面提到的是对单个样本求偏导和应用梯度下降算法的过程。对于有 m m m个样本的数据集,Cost Function J ( w , b ) J(w,b) J(w,b)、 a ( i ) a^{(i)} a(i) 和 权重参数 w 1 w_1 w1 的计算如图所示。
完整的Logistic回归中某次训练的流程如下,这里仅假设特征向量的维度为2:
J=0; dw1=0; dw2=0; db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;
接着再对 w 1 w_1 w1、 w 2 w_2 w2、 b b b进行迭代。
上述计算过程有一个缺点:整个流程包含两个for循环。其中:
- 第一个for循环遍历 m m m个样本
- 第二个for循环遍历所有特征
如果有大量特征,在代码中显示使用for循环会使算法很低效。向量化可以用于解决显式使用for循环的问题。
5.向量化(Vectorization)
继续以逻辑回归为例,如果以非向量化的循环方式计算 z = w T x + b z=w^Tx+b z=wTx+b,代码如下:
z = 0;
for i in range(n_x):
z += w[i] * x[i]
z += b
基于向量化的操作,可以并行计算,极大提升效率,同时代码也更为简洁:
(这里使用到python中的numpy工具库,想了解更多的同学可以查看ShowMeAI的 图解数据分析 系列中的numpy教程,也可以通过ShowMeAI制作的 numpy速查手册 快速了解其使用方法)
z = np.dot(w, x) + b
不用显式for循环,实现逻辑回归的梯度下降的迭代伪代码如下:
Z = w T X + b = n p . d o t ( w . T , x ) + b Z=w^TX+b=np.dot(w.T, x) + b Z=wTX+b=np.dot(w.T,x)+b
A = σ ( Z ) A=\sigma(Z) A=σ(Z)
d Z = A − Y dZ=A-Y dZ=A−Y
d w = 1 m X d Z T dw=\frac{1}{m}XdZ^T dw=m1XdZT
d b = 1 m n p . s u m ( d Z ) db=\frac{1}{m}np.sum(dZ) db=m1np.sum(dZ)
w : = w − σ d w w:=w-\sigma dw w:=w−σdw
b : = b − σ d b b:=b-\sigma db b:=b−σdb
参考资料
- 图解机器学习 | 逻辑回归算法详解
- 图解机器学习 | 机器学习基础知识)
- 图解AI数学基础 | 微积分与最优化)
- 图解数据分析
- numpy速查手册
ShowMeAI系列教程推荐
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程
- 机器学习实战:手把手教你玩转机器学习系列
- 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
推荐文章
- 深度学习教程 | 深度学习概论
- 深度学习教程 | 神经网络基础
- 深度学习教程 | 浅层神经网络
- 深度学习教程 | 深层神经网络
- 深度学习教程 | 深度学习的实用层面
- 深度学习教程 | 神经网络优化算法
- 深度学习教程 | 网络优化:超参数调优、正则化、批归一化和程序框架
- 深度学习教程 | AI应用实践策略(上)
- 深度学习教程 | AI应用实践策略(下)
- 深度学习教程 | 卷积神经网络解读
- 深度学习教程 | 经典CNN网络实例详解
- 深度学习教程 | CNN应用:目标检测
- 深度学习教程 | CNN应用:人脸识别和神经风格转换
- 深度学习教程 | 序列模型与RNN网络
- 深度学习教程 | 自然语言处理与词嵌入
- 深度学习教程 | Seq2seq序列模型和注意力机制