【人工智能-神经网络】Numpy 实现单层感知机对情感文本多分类

Numpy 实现单层感知机对情感文本多分类

一、 实验题目

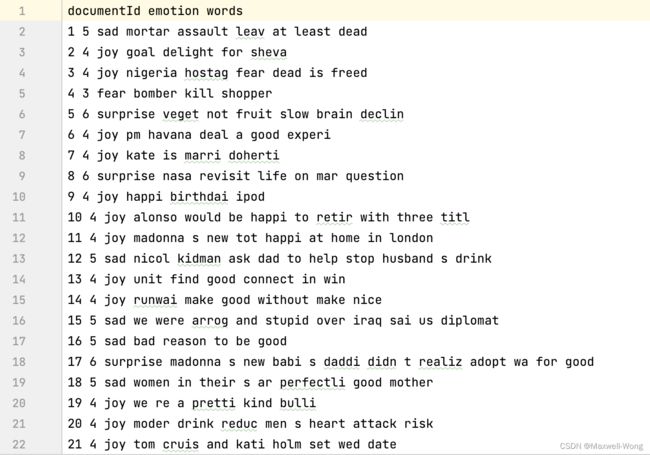
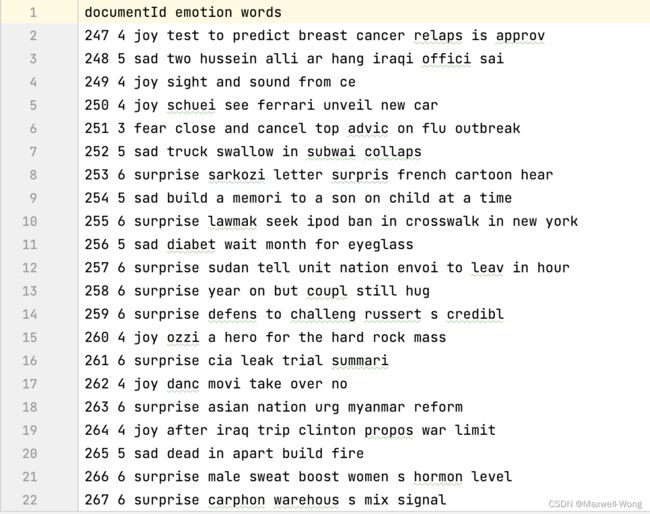
在给定文本数据集完成文本情感分类训练，在测试集完成测试，计算准确率

文本的特征可以使用TF或TF-IDF （可以使用sklearn库提取特征）设计合适的网络结构，选择合适的损失函数利用训练集完成网络训练，并在测试集上计算准确率。

训练集：train.txt

测试集: test.txt

二、 实验内容

1. 假定网络为单层感知机，且没有激活层，没有偏置，此时，网络输出为y=XW

2.设置损失函数为L_MSE，并随机初始化网络参数W

3.当满足终止条件时，终止优化，否则继续

4.计算网络输出y=XW，以及损失$$L_{MSE}=1/N(XW-Y{)}^T(XW-Y)$$

5.求导可得$\partial L_{MSE}/\partial W=1/N{X}^T(XW-Y)$

6.根据$W=W-\eta \partial L_{MSE}/\partial W$更新参数W

7.跳转到3

三、关键代码

from sklearn.feature_extraction.text import TfidfVectorizer
import numpy as np
from sklearn.preprocessing import LabelBinarizer
import matplotlib.pyplot as plt

train_set_path = 'train.txt'
test_set_path = 'test.txt'

'''
---------------Basic Concept---------------
1.   单层感知机 (输入层+输出层), 输入层为每个文本的特征值、输出层经过sigmoid函数, 为各类的预测值
2.   输入、输出、权重三者的关系为: Y = XW, 其中,X是(train_size, feature_size)的矩阵, W是(feature_size, class_num)的矩阵 
2.1. 需要注意的是, 由于输出经过了sigmoid函数, 因此值被限制在0～1之间, 而我们使用的标签是1~6的数, 所以要将它化成二进制码
3.   损失为L_MSE=1/N(XW−Y)^T(XW−Y) 对权重进行更新, 通过W = W - lr * ∂L_MSE/∂W, 其中∂L_MSE/∂W = 1/N X^T(XW−Y): [(feature_size, train_size) * (train_size, 6)]
3.1. 这里的Y是标签, 因为已经化成二进制值,所以每一个Yi是(1,6)的矩阵,如[0,0,0,1,0,0]表示标签4,

---------------END---------------

'''
# hyper parameters
learning_rate = 0.6
num_epochs = 4000
num_classes = 6
batch_size = 100
epochs = []
accur_train = []
accur_test = []


# 激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def dsigmoid(x):
    return x * (1 - x)


def data_process(path):
    '''
    :param path: 数据集路径
    :return: 文本、情感标签
    '''
    words = []
    data_set = []
    emotion = []
    with open(path, 'r') as F:
        line = F.readlines()
        for i in range(1, len(line)):
            emo = (int)(line[i].split()[1])  # 情感标签
            temp = line[i].split()[3:]
            out = ' '.join(temp)
            words.append(out)
            emotion.append(emo)
    return words, emotion


def tf_idf_cal(text):
    '''
    :param text: 待计算文本
    :return: 特征名称和特征值矩阵
    '''
    tf_idf_vec = TfidfVectorizer()
    tf_idf_matrix = tf_idf_vec.fit_transform(text)
    return tf_idf_vec.get_feature_names(), tf_idf_matrix.toarray()


words_train, emotion_train = data_process(train_set_path)
words_test, emotion_test = data_process(test_set_path)
train_feature_name, train_tf_idf = tf_idf_cal(words_train)
test_feature_name, test_tf_idf = tf_idf_cal(words_test)

# 处理训练集，将测试集特征在训练集中未出现过的特征值赋值为0
aligned_train_set = []
aligned_test_set = test_tf_idf
for k in range(len(train_tf_idf)):
    temp = []
    for i in range(len(test_feature_name)):
        feature = test_feature_name[i]
        if feature in train_feature_name:
            idx = train_feature_name.index(feature)
            temp.append(train_tf_idf[k][idx])
        else:
            temp.append(0)
    aligned_train_set.append(temp)


'''
方便查看：
---------------Basic Concept---------------
1.   单层感知机 (输入层+输出层), 输入层为每个文本的特征值、输出层经过sigmoid函数, 为各类的预测值
2.   输入、输出、权重三者的关系为: Y = XW, 其中,X是(train_size, feature_size)的矩阵, W是(feature_size, class_num)的矩阵 
2.1. 需要注意的是, 由于输出经过了sigmoid函数, 因此值被限制在0～1之间, 而我们使用的标签是1~6的数, 所以要将它化成二进制码
3.   损失为L_MSE=1/N(XW−Y)^T (XW−Y): [(6,train_size) * (train_size, 6)] 对权重进行更新, 通过W = W - lr * ∂L_MSE/∂W, 其中∂L_MSE/∂W = 1/N X^T(XW−Y): [(feature_size, train_size) * (train_size, 6)]
3.1. 这里的Y是标签, 因为已经化成二进制值,所以每一个Yi是(1,6)的矩阵,如[0,0,0,1,0,0]表示标签4,
     我们需要对Y进行扩展, 以便计算损失, 即将Y扩展成(train_size, 6)的矩阵,  

---------------END---------------

'''
def MSE(inputs, outputs, labels): # 这里的labels为(train_size, 6)的矩阵
    '''
    :param inputs: 特征矩阵 (train_size, feature_size)
    :param outputs: 网络输出 (train_size, num_class)
    :param labels: 标签 (train_size, num_class)
    :return: MES loss和它对W的偏导数
    '''
    n = outputs.shape[0] # train_size
    mse_loss = 0  # 所有样本的mse loss之和
    loss_mat = (outputs - labels) ** 2 / n  # 矩阵(train_size, train_size)
    for loss in loss_mat:
        mse_loss += loss.sum()
    loss_partial_mat = np.dot(inputs.T, (outputs - labels)) / n  # 矩阵(feature_size, num_class)
    return mse_loss, loss_partial_mat

'''
单层感知机
'''
class Perceptron:
    def __init__(self, in_size, out_size):
        self.in_size = in_size
        self.out_size = out_size
        self.weights = np.random.randn(in_size, out_size) # 随机化权重矩阵

    def forward(self, X):
        out = np.dot(X, self.weights)
        out = sigmoid(out)  # sigmoid函数，输出值被限制到0和1之间
        return out

# 转换成numpy数组
aligned_train_set = np.array(aligned_train_set)
aligned_test_set = np.array(aligned_test_set)
emotion_train = np.array(emotion_train)
emotion_test = np.array(emotion_test)

# 数值为1~6的情感标签转化成二进制
emotion_train_b = LabelBinarizer().fit_transform(emotion_train)
emotion_test_b = LabelBinarizer().fit_transform(emotion_test)

# 数据集参数
total_step = train_size = len(aligned_train_set)
test_size = len(aligned_test_set)
feature_size = len(aligned_train_set[0])



'''
Train the perceptron and Predict the label each batch
'''
perceptron = Perceptron(feature_size, num_classes)
for epoch in range(num_epochs):
    out = perceptron.forward(aligned_train_set)
    out_test = perceptron.forward(aligned_test_set)

    mse_loss, loss_partial_mat = MSE(aligned_train_set, out, emotion_train_b)
    perceptron.weights = perceptron.weights - learning_rate * loss_partial_mat
    if epoch % batch_size == 0:
        pre_label = []
        for i in range(out.shape[0]):
            pre_label.append(np.argmax(out[i]) + 1)
        accuracy = np.mean(np.equal(pre_label, emotion_train))
        print('Train_Set: Epoch [{}/{}], Loss: {:.4f}, Accuracy: {}'.format(epoch + 1, num_epochs, mse_loss,
                                                                            100 * accuracy))
        accur_train.append(100 * accuracy)

        pre_label = []
        for i in range(out_test.shape[0]):
            pre_label.append(np.argmax(out_test[i]) + 1)
        accuracy = np.mean(np.equal(pre_label, emotion_test))
        print('Test_Set: Epoch [{}/{}], Loss: {:.4f}, Accuracy: {}'.format(epoch + 1, num_epochs, mse_loss,
                                                                            100 * accuracy))
        epochs.append(epoch)
        accur_test.append(100 * accuracy)

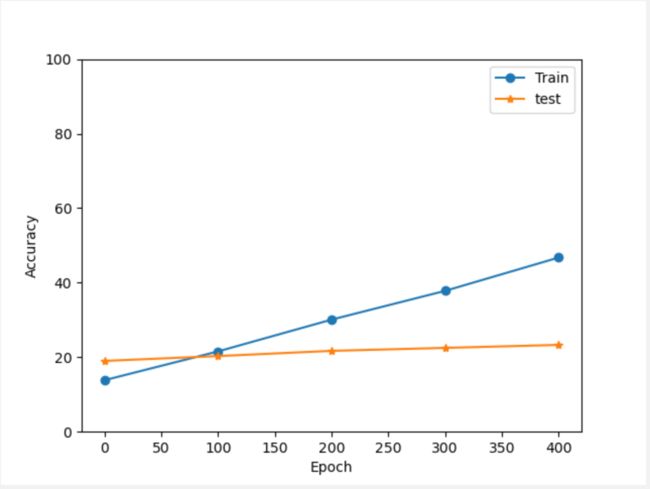
plt.ylim((0, 100))
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.plot(epochs, accur_train, marker='o')
plt.plot(epochs, accur_test, marker='*')
plt.legend(['Train', 'test'])
plt.show()

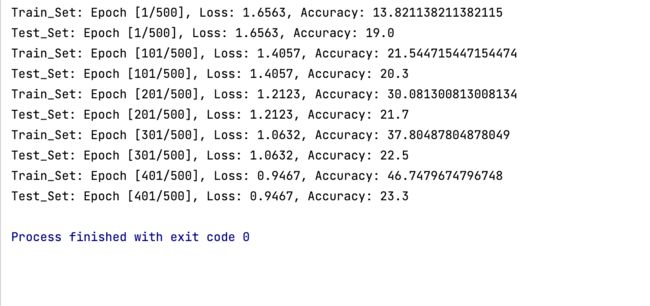
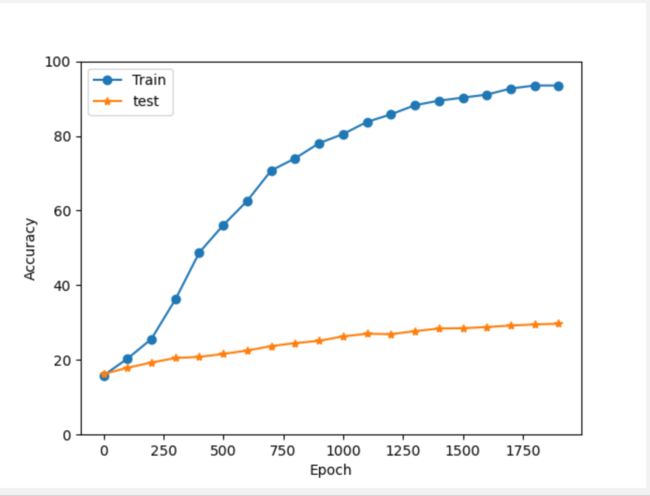
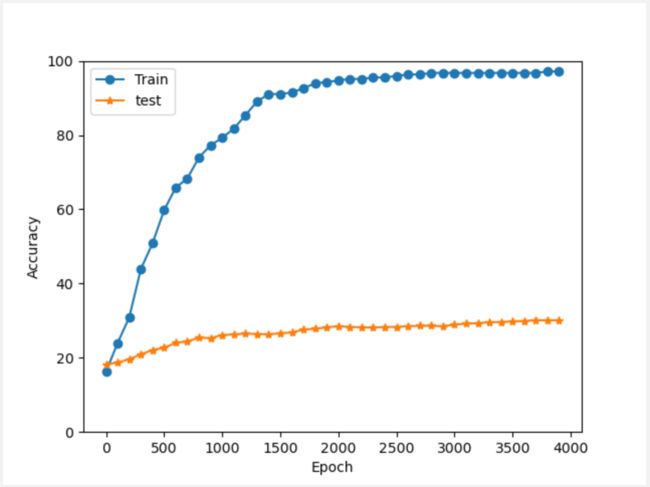
四、实验结果：

通过numpy矩阵进行运算速度还是很快的，基本在几秒内就能够算出结果。

(1) Epoch 500

(2) Epoch 2000

(3) Epoch 4000