实战NLP beginner任务一:基于机器学习的文本分类

一.理论知识

1.1 Ngram

1.1.1 什么是Ngram

Ngram的基本是将一个句子划分为每个单词序列长度为N的序列集合。例如：

i am a student

使用2-gram后的结果是

{i am} , {am a} , {a student}

若使用3-gram，则结果为

{i am a} , {am a student}

1.1.2 为什么使用Ngram

在传统的语句评估模型中，若只考虑单个单词，例如将例句划分为

{i} , {am} , {a} , {student}

这样划分的结果是模型无法学习到单词与单词之间的关系，导致 i am a student 的结果与student a i am 是相同的。

而如果一个单词考虑全部它之前的单词，会导致与该单词无关的单词被计算到其中，例如i am a student, but you are a pig 如 pig 显然是只和 you 相关的，而与前面的i am a student无关，过多地考虑之前的单词反而会使评估模型的评估能力下降。

让我们从概率论的角度再看
如果评估一个单词与该单词之前的所有单词有关，则有
$p(x_1,x_2,x_3,.....,x_n)=p(x_1)\ast p(x_2|x_1)...\ast p(x_n|x_1,x_2,.....x_{n-1})$
会导致第n个单词的概率趋近于0

而如果我们采用2-gram去评估一个单词的话，该单词的概率则为：
$p(x_1,x_2,x_3,.....,x_n)=p(x_n|x_{n-1})$

1.1.3 N-gram的应用

• ci=词性标注
• 垃圾短信分类
• 分词器
• 机器翻译和语音识别

1.1.4 N-gram存在的问题及解决方法

存在问题：

稀疏问题：出现概率为0的可能性很大，导致大部分句子概率为0
解决方法：

数据平滑：使所有N-gram概率之和为1，所有N-gram的概率都不为0

1. add-one：即强制让所有的n-gram至少出现一次，只需要在分子和分母上分别做加法即可。$p(x_n|x_{n-1}=\frac{C(x_{n-1}{x}_n)+1}{C(x_{n-1})+|V|})$
2. add-k: 原本是加一，现在加上一个小于1的常数K。$p(x_n|x_{n-1}=\frac{C(x_{n-1}{x}_n)+k}{C(x_{n-1})+k|V|})$
3. 回溯：尽可能地用最高阶组合计算概率，当高阶组合不存在时，退而求其次找次低阶。
   $p(x_n|x_{n-k},x_{n-k+1},.....x_{n-1})=\{\begin{array}{l}p(x_n|x_{n-k},x_{n-k+1},.....x_{n-1})\\ \alpha (x_{n-1}...x_{n-k})\ast p(x_n|x_{n-k+1},x_{n-k+2},.....x_{n-1})\end{array}$

1.2 bag of words(BOWs)

1.2.1 什么是BOWs

Bag of words 是一种文本建模的自然语言处理技术。从技术上讲，我们可以说它是一种利用文本数据进行特征提取的方法。这种方法是一种从文档中提取特征的简单而灵活的方法。
Bag是描述文档中出现的词的文本表示。我们只记录字数，而忽略语法细节和词序。它被称为单词“包”，因为有关文档中单词顺序或结构的任何信息都被丢弃了。该模型只关注文档中是否出现已知单词，而不关注文档中的哪个位置。

1.2.2 怎么使用BOWs

我们举例来说明怎么使用BOWs
现在我们有两个句子

• 句子1：welcome to my blog, now start learning
• 句子2：learning is a good practice

我们将这两个句子划分为单词序列：

句子1	句子2
welcome	learning
to	is
my	a
blog	good
now	practise
start
learning

我们列出所有的单词序列

welcome	to	my	blog	now	start	learning	is	a	good	practise

我们根据划分好的单词序列将两个句子编码：

单词序列	句子1编码	句子2编码
welcome	1	0
to	1	0
my	1	0
blog	1	0
now	1	0
start	1	0
learning	1	1
is	0	1
a	0	1
good	0	1
practise	0	1

句子1编码后的结果为$（1,1,1,1,1,1,1,0,0,0,0）$
句子2编码后的结果为$(0,0,0,0,0,0,1,1,1,1,1)$

这种编码方式只考虑了句子中的单词是否在单词序列中出现，没有考虑到每个单词出现的频率问题，而在大部分句子中出现频率高的单词如to,is,a等单词对整个句子的语义影响并不大，因此我们可以先统计出每个单词出现的频率，在后续处理中可以去掉高频词。

这样我们的单词字典变成了：

单词序列	频率
welcome	1
my	1
blog	1
now	1
start	1
learning	2
good	1
practise	1

句子1编码后的结果为$（1,1,1,1,1,2,0,0）$
句子2编码后的结果为$(0,0,0,0,0,2,1,1)$

该方法是BOWs技术中常用的方法，原因是机器学习中使用的数据集非常大，可以包含几千甚至几百万个单词的词汇。因此，在使用词袋之前对文本进行预处理是一种更好的方法。

1.3 logistic/softmax 回归

1.3.1 什么是逻辑回归

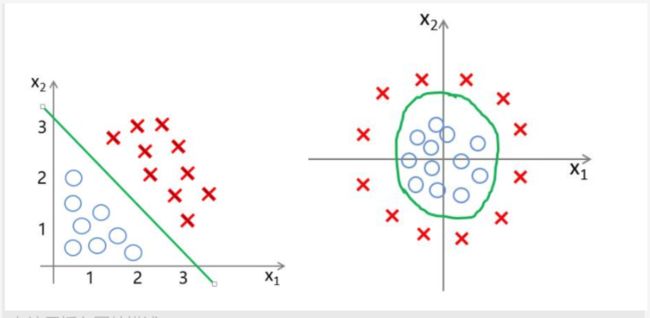
利用逻辑回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类（主要用于解决二分类问题）。-----《机器学习实战》

逻辑回归的主要找到一条曲线对数据进行二分类。如图：

以上两幅图分别对应着，当分类样本具有两个特征值 $x_1$,$x_2$ 时，样本可进行线性可分，以及非线性可分的情况。而逻辑回归寻找的曲线，便是图中所示的绿色直线与绿色曲线。

1.3.2 逻辑回归模型

我们假设需要寻找的曲线为：
$f(x^{(i)})={\theta }_0+{\theta }_1{x}_1^{(i)}+{\theta }_2{x}_2^{(i)}+{\theta }_3{x}_3^{(i)}+....{\theta }_n{x}_n^{(i)}$

我们令 $\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ {\theta }_3\\ .\\ .\\ {\theta }_n\end{array}\right]$ $x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2\\ x_3^{(i)}\\ .\\ .\\ x_n^{(i)}\end{array}\right]$ 其中$x_0=1$，$(x_1,x_2...x_n)$表示特征值，$i=(1,2,3,...m)$，$m$表示样本数，那么$f(x^{(i)})={\theta }^T{x}^{(i)}$。

 
然后将$z=f(x)$经过$sigmoid$函数，即$y=h(z)$得到最终的预测结果，其中
$$h(z)=\frac{1}{1+e^{-z}}$$
综上所述，我们的logistic回归模型函数为
$$h({\theta }^T{x}^{(i)})=\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}$$

1.3.3 逻辑回归的损失函数

对于逻辑回归模型函数，我们最终表达的是样本为"1"的概率，也就是说：
$$p(y=1|x^{(i)},\theta )=h({\theta }^T{x}^{(i)})$$
则样本为0的概率为:
$$p(y=0|x^{(i)},\theta )=1-h({\theta }^T{x}^{(i)})$$
$p(y=1|x^{(i)},\theta )$表示样本为1的概率，$p(y=0|x,\theta )$表示样本为0的概率，综上，我们可以得到：
$$p(y|x^{(i)},\theta )=p(y=1|x^{(i)},\theta {)}^{y}p(y=0|x^{(i)},\theta {)}^{1-y}=h({\theta }^T{x}^{(i)}{)}^y(1-h({\theta }^T{x}^{(i)}){)}^{1-y}$$
我们可以得到 $\theta$ 的似然函数为:
$$L(\theta )=\prod _{i=1}^{m}p(y|x^{(i)},\theta )=\prod _{i=1}^{m}h({\theta }^T{x}^{(i)}{)}^y(1-h({\theta }^T{x}^{(i)}){)}^{1-y}$$
对等式取对数，得到
$$logL(\theta )=\sum _1^{m}log(p(y|x^{(i)},\theta ))=\sum _1^{m}ylog(h({\theta }^T{x}^{(i)}))+(1-y)log((1-h({\theta }^T{x}^{(i)}))$$
我们令损失函数：
$$J(\theta )=-\frac{1}{m}\sum _1^{m}ylog(h({\theta }^T{x}^{(i)}))+(1-y)log((1-h({\theta }^T{x}^{(i)}))$$

1.3.4 优化算法

我们用梯度下降法，对参数$\theta$进行优化，具体梯度下降法可参考神经网络的前向传播与反向传播及用numpy搭建神经网络
简而言之，参数$\theta$的更新方法为：
$${\theta }_j={\theta }_j-\alpha \frac{\partial J}{\partial \theta }$$
$\alpha$为学习率，是超参数。
而损失函数$J$关于$\theta$的偏导数为：
$$\frac{\partial J}{\partial \theta }=-\frac{1}{m}\sum _1^m[y^{(i)}-h({\theta }^T{x}^{(i)})]\cdot x^{(i)}=\frac{1}{m}\sum _1^m[h({\theta }^T{x}^{(i)})-y^{(i)}]\cdot x^{(i)}$$

1.3.5 softmax回归

softmax回归模型函数：
逻辑回归针对是的二分类问题，而softmax回归针对的是多分类问题。
对于输入数据$\{(x_1,y_1),(x_2,y_2),(x_3,y_3),....(x_n,y_n)\}$有 $k$个类别，即$y_i\in \{1,2,3...k\}$，那么 softmax 回归主要估算输入数据$x_i$ 归属于每一类的概率，即
$$h(x^{(i)})=\left[\begin{array}{c}p(y^{(i)}=1|x^{(i)},\theta )\\ p(y^{(i)}=1|x^{(i)},\theta )\\ p(y^{(i)}=2|x^{(i)},\theta )\\ .\\ .\\ .\\ p(y^{(i)}=k|x^{(i)},\theta )\end{array}\right]=\frac{1}{{\sum }_1^k{e}^{{\theta }_j^T{x}^{(i)}}}\left[\begin{array}{c}{e}^{{\theta }_1^T{x}^{(i)}}\\ e^{{\theta }_2^T{x}^{(i)}}\\ e^{{\theta }_3^T{x}^{(i)}}\\ .\\ .\\ .\\ e^{{\theta }_k^T{x}^{(i)}}\end{array}\right]$$
其中，$\{{\theta }_1,{\theta }_2,...,{\theta }_k\in \theta \}$是模型的参数，乘以$\frac{1}{{\sum }_1^k{e}^{{\theta }_j^T{x}^{(i)}}}$是为了让概率位于[0,1]并且概率之和为 1,softmax 回归将输入数据$x_i$归属于类别 j 的概率为
$$p(y_i=j|x_i,\theta )=\frac{e^{{\theta }_j^T{x}^{(i)}}}{{\sum }_{l=1}^k{e}^{{\theta }_l^T{x}^{(i)}}}$$

softmax的损失函数：

$$L(\theta )=-\frac{1}{m}[\sum _{i=1}^m\sum _{j=1}^k(y_i=j)log\frac{e^{{\theta }_j^T{x}^{(i)}}}{{\sum }_{l=1}^k{e}^{{\theta }_l^T{x}^{(i)}}}]$$
softmax的优化算法

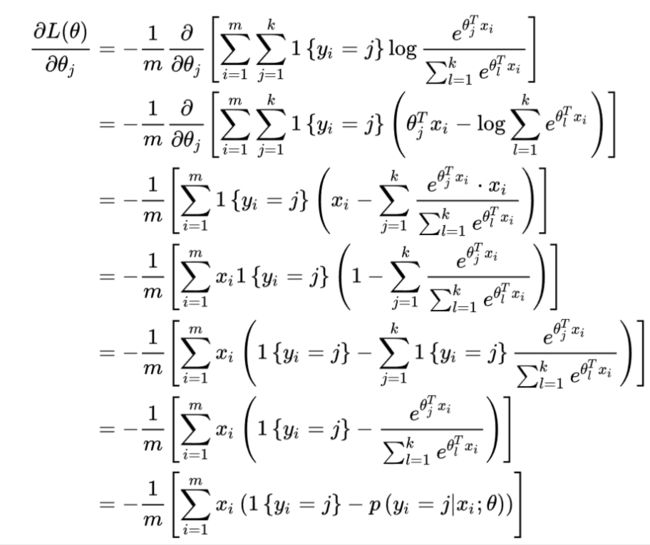
二.numpy实现

2.1 Ngram实现

from collections import Counter
#用csr_matrix来压缩稀疏行矩阵
from scipy.sparse import csr_matrix
import numpy as np
class Ngram():
    def __init__(self, n_grams, max_tf=0.8):
        ''' n_grams: tuple'''
        self.n_grams = n_grams
        self.tok2id = {}
        self.tok2tf = Counter()
        self.max_tf = max_tf

    @staticmethod
    def tokenize(text):
        ''' In this task, we simply the following tokenizer.'''
        """将一个句子的字符串变为单词的列表"""
        return text.lower().split(" ")

    def get_n_grams(self, toks):
        '''将句子划分为长度为(1,n)的单词序列 例如"i love you",长度为(1,2)，则输出为["i","love","you","i love","love you"]'''
        ngrams_toks = []
        for ngrams in range(self.n_grams[0], self.n_grams[1] + 1):
            for i in range(0, len(toks) - ngrams + 1):
                ngrams_toks.append(' '.join(toks[i:i + ngrams]))
        return ngrams_toks

    def fit(self, datas, fix_vocab=False):
        ''' Transform the data into n-gram vectors. Using csr_matrix to store this sparse matrix.'''
        if not fix_vocab:
            for data in datas:
                #将句子变换为单词列表
                toks = self.tokenize(data)
                #将单词列表变成单词序列
                ngrams_toks = self.get_n_grams(toks)
                #统计单词出现的频率
                self.tok2tf.update(Counter(ngrams_toks))
            #过滤掉高频词
            self.tok2tf = dict(filter(lambda x: x[1] < self.max_tf * len(datas), self.tok2tf.items()))
            #将每个单词序列编号
            self.tok2id = dict([(k, i) for i, k in enumerate(self.tok2tf.keys())])
        # the column indices for row i are stored in indices[indptr[i]:indptr[i+1]]
        # and their corresponding values are stored in nums[indptr[i]:indptr[i+1]]
        #用indices来保存每个单词序列，nums保存单词序列对应的编号，indptr保存单词序列的长度，最后用csr_matrix来压缩存储
        indices = []
        indptr = [0]
        nums = []
        for data in datas:
            toks = self.tokenize(data)
            ngrams_counter = Counter(self.get_n_grams(toks))
            for k, v in ngrams_counter.items():
                if k in self.tok2id:
                    indices.append(self.tok2id[k])
                    nums.append(v)
            indptr.append(len(indices))
        return csr_matrix((nums, indices, indptr), dtype=int, shape=(len(datas), len(self.tok2id)))

2.2 bag of words 的实现

def reg_text(text):
	"""
	将text转化为单词序列：
	如"you are a pig"->["you" "are" "a" "pig"}
	"""
    token = re.compile('[A-Za-z]+|[!?.,()]')
    newtext = token.findall(text)
    newtext = [word.lower() for word in newtext]
    return newtext

def BOWs(data,row_name):
    """
    实现bag of words
    :param data: 需要变化的数据，格式一般是dataframe
    :param row_name:需要变化列的名称
    :return:返回变化后的结果
    """
    data[row_name] = data[row_name].apply(reg_text)
    word_dict = {}
    for name in data[row_name]:
        for word in name:
            if word in word_dict:
                word_dict[word] += 1
            else:
                word_dict[word] = 1
    word_list = list(word_dict)
    for i in range(len(data)):
        print(i,len(data))
        new_text = np.zeros((len(word_dict)))
        for word in data.loc[i,row_name]:
            new_text[word_list.index(word)] = word_dict[word]
        data.loc[i,row_name] = str(new_text)

    print(data)
    return data

2.3 logistic回归的numpy实现

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

class LogisticRegression():
    def __init__(self,num_features,learning_rate = 0.01,regularization = None,c = 1):
         self.w = np.random.uniform(size = num_features)
         self.learning_rate = learning_rate
         self.num_features = num_features
         self.regularization = regularization
         self.c = c

    def _exp_dot(self,x):
        return np.exp(x.dot(self.w))

    def predict(self,x):
        """
        Return the predicted classes.
        :param x: (batch_size, num_features)
        :return: batch_size)
        """
        probs = sigmoid(self._exp_dot(x))
        return (probs > 0.5).astype(np.int)

    def Gradients(self,x,y):
        """
        Perform one gradient descent.
        :param x: (batch_size, num_features)
        :param y: (batch_size)
        :return: None
        """
        probs = sigmoid(self._exp_dot(x))
        #print(self.w.shape,x.shape,y.shape)
        gradients = (x.multiply((y - probs).reshape(-1,1))).sum(0)
        gradients = np.array(gradients.tolist()).reshape(self.num_features)

        if self.regularization == "l2":
            self.w += self.learning_rate * (gradients * self.c - np.sign(self.w))
        else:
            self.w += self.learning_rate * gradients

    def mle(self,x,y):
        """return the mle estimates,log[p(y|x)]"""
        return (y * x.dot(self.w) - np.log(1 + self._exp_dot(x))).sum()

2.4 softmax回归的numpy实现

import numpy as np

def softmax(x):
    return np.exp(x) / np.exp(x).sum(-1,keepdims = True)

def to_onehot(x,class_num):
    return np.eye(class_num)[x]

class SoftmaxRegression():
    def __init__(self,num_features,num_classes,learning_rate = 0.01,regularization = None, c = 1):
        self.w = np.random.uniform(size=(num_features,num_classes))
        self.learning_rate = learning_rate
        self.num_features = num_features
        self.num_classes = num_classes
        self.regularization = regularization
        self.c = c

    def predict(self,x):
        '''
        Return the predicted classes.
        :param x: (batch_size, num_features)
        :return: (batch_size)
        '''
        probs = softmax(x.dot(self.w))
        return probs.argmax(-1)

    def Gradients(self,x,y):
        '''
        Perform one gradient descent.
        :param x:(batch_size, num_features)
        :param y:(batch_size)
        :return: None
        '''
        probs = softmax(x.dot(self.w))
        gradients = x.transpose().dot(to_onehot(y,self.num_classes) - probs)
        if self.regularization == "l2":
            self.w += self.learning_rate * (gradients * self.c - self.w)
        elif self.regularization == "l1":
            self.w += self.learning_rate * (gradients * self.c - np.sign(self.w))
        else:
            self.w += self.learning_rate * gradients
    def mle(self, x, y):
        '''
        Perform the MLE estimation.
        :param x: (batch_size, num_features)
        :param y: (batch_size)
        :return: scalar
        '''
        probs = softmax(x.dot(self.w))
        return (to_onehot(y, self.num_classes) * np.log(probs)).sum()

参考

• 逻辑回归理解及代码实现
• softmax回归原理及理解
• 自然语言处理NLP中的N-gram模型
• code for nlp beginner