MATLAB常见非线性可视化绘制方法-分岔图与庞加莱截面(混沌可视化、Poincare截面、Logistic、Henon、Lorenz、Rossler、Duffing系统)
MATLAB常见非线性可视化绘制方法-分岔图与庞加莱截面(混沌可视化、Poincare截面、Logistic、Henon、Lorenz、Rossler、Duffing系统)
- 1 引言
- 2 离散非线性系统的分岔图绘制
-
- 2.1 一维Logistic系统分岔图
- 2.2 二维Henon系统分岔图
- 3 庞加莱截面
-
- 3.1 绘制思路
- 3.2 利用频闪法快速绘制
- 4 非线性系统的分岔图
-
- 4.1 Duffing系统分岔图
- 4.2 Rossler系统分岔图
- 4.3 Lorenz系统分岔图
本文首发于 matlab爱好者 微信公众号,欢迎关注。
惯例声明:本人没有相关的工程应用经验,只是纯粹对相关算法感兴趣才写此博客。所以如果有错误,欢迎在评论区指正,不胜感激。本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。
1 引言
本文大概介绍一下常用的非线性可视化的方法,由于篇幅问题,分了两章。第一篇介绍一下相图与相空间的概念。第二篇介绍一下庞加莱截面和分岔图的绘制方法。后面第三篇就不打算写可视化了,看看要不要写一个频谱分析、李雅普诺夫指数分析、维数分析之类的时间序列分析,但这一部分有趣性不高,实在没动力o(╥﹏╥)o。
非线性的数学研究诞生时间还是比较久了,从蝴蝶效应开始一直到现在,常用的分析方法变化不是太大。各领域研究方向有所不同,但在论文中如果涉及到方程的非线性,总会需要定性的分析一下,由于方法比较类似,所以常常也可以参阅别的领域的非线性分析相关的方法或者好看的绘图方式。
这篇博客主要讲怎么绘制分岔图,顺便也提了一下怎么绘制庞加莱截面。分岔一般指的是系统中某一个常数发生变化,导致整个系统都会随之改变的现象。在电路中可能是某个电容改变,在机械系统中可能是某个轴承摩擦阻力的变化,在流场中可能是风速的改变。这些参数微小的变化,就会导致系统突然性情大变,变得震荡发散不收控制。
上一篇介绍了相图的绘制,这个可以看做是非线性可视化的基础,建议先看一眼上一篇文章:
MATLAB常见非线性可视化绘制方法-相图与相空间https://blog.csdn.net/weixin_42943114/article/details/123193855
参考目录
[1]Morris W. Hirsch. 微分方程、动力系统与混沌导论[M]. 人民邮电出版社, 2008.
[2]刘秉正. 非线性动力学与混沌基础[M]. 东北师范大学出版社, 1994.
[3] Khalil H K . 非线性系统(第3版)[M].电子工业出版社,2005.
[4]Morris W. Hirsch. Differential equations, dynamical systems, and an introduction to chaos [M] Academic Press
[5] 微分方程、动力系统与混沌导论[M]
[6] 计算物理基础-第10章第77讲(北京师范大学)(中国大学MOOC)计算物理基础_北京师范大学_中国大学MOOC(慕课) (icourse163.org)
[7]Computing accurate Poincaré maps[J]. PHYSICA D, 2002, 171(3):127-137.
[8]Santo Banerjee. Applications of Chaos and Nonlinear Dynamics in Engineering[M]. Springer, 2011
[9]Ali.H.Nayfeh. Applied Nonlinear Dynamics Analytical, Computational, and Experimental Methods[M]. 1995.(用到了P284里面的Henon系统)
[10]詹姆斯·格雷克. 混沌:开创新科学[M].
2 离散非线性系统的分岔图绘制
2.1 一维Logistic系统分岔图
Logistic系统是一种非常简单的二次多项式形式的映射。该映射是1976 年生物学家罗伯特·梅 (Robert May) 发扬光大的,用来说明即使很简单的系统也可以产生混沌现象。其迭代方程如下:
x n + 1 = a ( 1 − x n ) x n x_{n+1}=a(1-x_n)x_n xn+1=a(1−xn)xn
这个迭代方程用来表述某个物种的数量增长变化。其中x的含义为现有物种数量除以理论最大数量,a为增长率。方程认为,物种数量的变化,与物种现存人口x有关,也与人口过多带来的环境压力(1-x)有关。
当增长率a小于1时,物种逐渐灭亡;当增长率在1-3之间,则物种能够稳定在一个范围内;当增长率更大,则会逐渐出现非线性现象。
绘制其分岔图有两种方法:
第一种,均匀分布初始点,然后进行逐次迭代,观察其运动规律。
比如下图选取a=2.1和a=3.3的两个参数,初始分布各个初值,进行迭代,观察这些初值的变化:

可以看到当a=2.1时,最终所有种群收敛到了1个点。当a=3.3时,最终所有种群点收敛到了2个点。
继续细化a的值,列出一个图,可以看到不同参数a变化下,系统的收敛规律:
最终迭代200次的结果如下图:
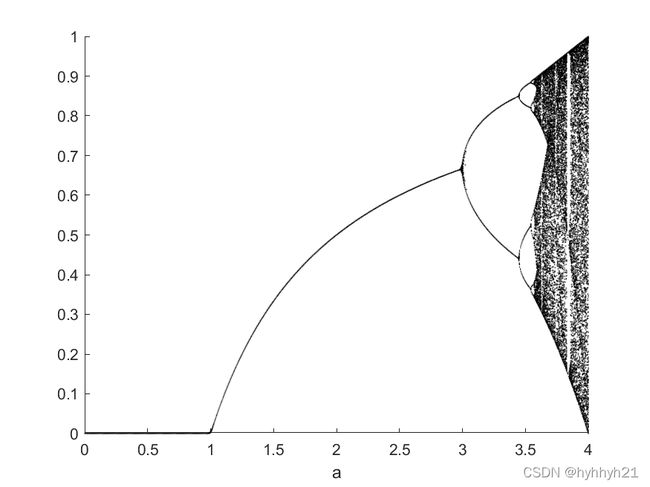
这种体现随着某个参数(比如a)变化,导致系统行为发生改变的图,叫做分岔图。
当然为了好看,也可以根据点的密度来加一点颜色,比如下面这个样子。
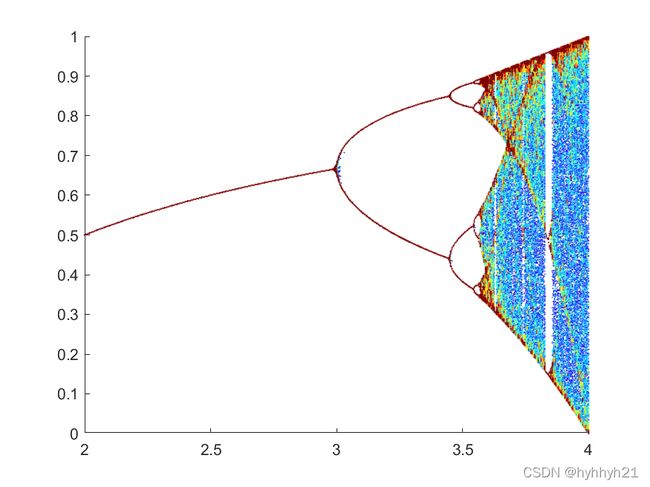
上面几个图的代码如下:
clear
clc
close all
%分岔图
%离散系统
%% 1Logistic系统
%% 1.1Logistic系统 两个典型的a,进行迭代的效果
d=0.004;
x=d:d:1-d;
Nx=length(x);
BF=zeros(1,Nx);
a1=2.1;
a_k1=a1;%第一个a=2.1
a2=3.3;
a_k2=a2;%第二个a=3.3
x1=x;
x2=x;
%在系统中迭代50次
for m=1:50
%把结果绘图
f1=figure(1);
set(f1,'Color',[1,1,1])
clf
subplot(1,2,1)
plot(a1*ones(size(x1)),x1,'.')
ylim([0,1])
text(a1-0.8,0.5,['a1=',num2str(a1)])
text(a1-0.8,0.4,['迭代次数',num2str(m)])
subplot(1,2,2)
plot(a2*ones(size(x1)),x2,'.')
ylim([0,1])
text(a2-0.8,0.5,['a2=',num2str(a2)])
text(a2-0.8,0.4,['迭代次数',num2str(m)])
pause(0.1)
%更新下一次迭代
x1=Logistic(x1,a_k1);
x2=Logistic(x2,a_k2);
end
%% 1.2 不同a,绘制分岔图
%初始种群采用均匀分布
d=0.005;
x=d:d:1-d;
a=0:0.004:4;%把a采集的足够密,就可以绘制随参数a变化的分岔图
Nx=length(x);
Na=length(a);
BF=zeros(Na,Nx);%初始化最终储存的矩阵
for k=1:Na
a_k=a(k);
x1=x;
%在系统中迭代200次
for m=1:200
x1=Logistic(x1,a_k);
end
%把结果保存
BF(k,:)=x1;
end
%画图
figure()
hold on
for k=1:Na
a_k=a(k);
plot(a_k*ones(1,Nx),BF(k,:),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
xlabel('a')
%% 1.3 不同a 动图,把上面那个分岔图的过程展示出来
d=0.005;
x=d:d:1-d;
a=0:0.004:4;
Nx=length(x);
Na=length(a);
BF=ones(Na,1)*x;
BFx=a'*ones(1,Nx);
%在系统中迭代100次
for m=1:90
%绘制图片
f3=figure(3);
clf
scatter(BFx(:),BF(:),0.5,'k','MarkerEdgeAlpha',0.5)
text(0.7,0.6,['迭代次数',num2str(m)])
xlabel('a')
ylabel('x')
set(f3,'Color',[1,1,1])
pause(0.1)
%迭代更新
for k=1:Na
a_k=a(k);
x1=BF(k,:);
x1=Logistic(x1,a_k);
%把结果保存
BF(k,:)=x1;
end
end
%% 1.4 不同a上颜色
d=0.002;
x=d:d:1-d;
a=0:0.002:4;
Nx=length(x);
Na=length(a);
BF=zeros(Na,Nx);
for k=1:Na
a_k=a(k);
x1=x;
%在系统中迭代250次
for m=1:250
x1=Logistic(x1,a_k);
end
%把结果保存
BF(k,:)=x1;
end
%上颜色
BF_C=zeros(size(BF));
for k=1:Na
BF_k=BF(k,:);
[N,~,bin] = histcounts(BF_k,[0:0.01:1]);%统计每个小区间,点的数量,作为颜色
BF_C(k,:)=N(bin);%记录各个点的颜色
end
BFy=BF;
BFx=a'*ones(1,Nx);
figure()
scatter(BFx(:),BFy(:),0.5,BF_C(:),'MarkerEdgeAlpha',0.5)
caxis([0,20])
colormap(jet)
ylim([0,1]);
xlim([2,4]);
%% 后置函数
function x2=Logistic(x1,a)
%Logistic系统
%x(n+1)=a*(1-x(n))*x(n)
x2=a*(1-x1).*x1;
end
前面说分岔图绘制方法有两种,那么第二种,就是选取一个随机的初始点进行迭代,然后取它最后200次的历史位置(或者说运动过程),作为分岔图,而不是最终时刻的所有点的所有位置。
这种方式的优点是计算快,初始点只选取一个就可以,不需要上面动用200个点一起迭代。
代码如下,具体代码差别可以和上面方法1中的代码1.2进行对比:
%% 2.1 换一种计算方法
%初始化
a=0:0.004:4;
Nx=200;%最终储存最后200个点
Na=length(a);
BF=zeros(Na,Nx);
for k=1:Na
a_k=a(k);
x0=0.234;%随便初始一个点
for m=1:100 %先初始100步,来排除初始点选取的干扰
x0=Logistic(x0,a_k);
end
xs=zeros(1,Nx);%再正式开始循环,记录下一个点在迭代时候每一个位置
for m=1:Nx
x2=x0;
x0=Logistic(x2,a_k);
xs(m)=x2;
end
%把结果保存
BF(k,:)=xs;
end
%画图%这里用scatter还是plot函数绘图都行
figure()
hold on
for k=1:Na
a_k=a(k);
plot(a_k*ones(1,Nx),BF(k,:),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
xlabel('a')
ylabel('x')
%% 后置函数
function x2=Logistic(x1,a)
%Logistic系统
%x(n+1)=a*(1-x(n))*x(n)
x2=a*(1-x1).*x1;
end
因为该收敛的终究会收敛,该分岔的也会分岔,该混沌的依然会混沌,这是系统自己的行为特性,和初始选取的点无关。
另外,再多啰嗦一句,Logistic系统有一个非常典型的倍周期分岔特性,也就是分岔图的那根线,由1个分成了2个,2个分成了4个,4个又变成了8个,然后分岔的速度越来越快,直到进入混沌状态。这里2个岔代表在迭代结果在两个点上来回变动,周期为2;同理4个岔代表点在4个点上来回跳动,周期为4。这就是我个人对倍周期分岔的一个比较形象的解释。
2.2 二维Henon系统分岔图
Henon系统由 Michel Hénon大概在20世纪六七十年代,作为Lorenz模型的 Poincaré截面的简化模型引入。因此,我也准备将其作为衔接离散系统与庞加莱截面的一个关键切入口。
所以这一小节,用来如何用二维离散系统来绘制分岔图。
Henon系统有两个变量x和y,其迭代公式为:
x n + 1 = 1 + y n − a ∗ x n 2 y n + 1 = b ∗ x n x_{n+1}=1+y_n-a*x_n^2 \\ y_{n+1}=b*x_n xn+1=1+yn−a∗xn2yn+1=b∗xn
这里我们取b=0.3,则系统的可变参数只剩下a。
当a=0.2时,整个系统最终稳定到(x=1.09,y=3.27)这个点上。当a=0.95时,系统则在4个点上来回周期运动。当a=1.38时,系统则会陷入混沌。
下图可以看到当取不同a值时,系统的最终形式。

那么如何将这个二维的结果图转换到分岔图上呢?在前面一维的Logistic系统分岔图中,纵轴直接就是x。而对于二维离散结果,我们需要先投影到一维结果上,再绘制分岔图。
简单一点,可以直接投影的y轴上,我们用系统的y值来绘制分岔图;或者投影到x轴上,用系统的x值绘制分岔图。(或者投影到某个特殊的线上,不过一般简单点就直接投影到轴上了)


可以看到,除了形状可能会稍微有点不同,其分岔点的位置和分岔后的形态是完全一致的。
因此,对于二维系统或更高维系统的分岔图,只需要把离散点投影到一个轴上就可,不影响系统分岔点的分析和判断。
绘图代码如下。这里由于二维计算量较大,所以直接用的是第二种方法,也就是只选取一个初始点进行迭代,然后记录过程。
clear
clc
close all
%分岔图
%离散系统
%% 2 Henon系统
a=0:0.0016:1.4;
%采用直接截取迭代中间过程,作为分岔图
NT=300;%选取最后300次结果
Na=length(a);
BF_x=zeros(Na,NT);
BF_y=zeros(Na,NT);
for k=1:Na
a_k=a(k);
%初始值取0
x1=0;
y1=0;
%先初始迭代200次,避免初始值选取引起的干扰
for m=1:200
[x1,y1]=Henon(x1,y1,a_k,0.3);
end
%然后再迭代300次,作为要保存的结果
for m=1:NT
[x1,y1]=Henon(x1,y1,a_k,0.3);
%把结果保存
BF_x(k,m)=x1;
BF_y(k,m)=y1;
end
end
%分岔图1,用y绘图
figure()
hold on
for k=1:Na
a_k=a(k);
plot(a_k*ones(1,NT),BF_y(k,1:NT),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
xlabel('a')
ylabel('y')
%分岔图2,用x绘图
figure()
hold on
for k=1:Na
a_k=a(k);
plot(a_k*ones(1,NT),BF_x(k,1:NT),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
xlabel('a')
ylabel('x')
ylim([-1.5,2])
%绘制典型情况的最终x-y图
figure()
aa=[0.2,0.95,1.036,1.076,1.08,1.38];%要展示的aa图
for k=1:6
subplot(2,3,k)
[~,Ind_a]=min(abs(a-aa(k)));
plot(BF_x(Ind_a,:),BF_y(Ind_a,:),'LineStyle','none','Marker','.')
xlim([-1.5,1.5])
ylim([-0.4,0.4])
xlabel('x');ylabel('y');
title(['a=',num2str(aa(k))])
end
%% 后置函数
function [x2,y2]=Henon(x1,y1,a,b)
%Henon系统
%x(n+1)=1+y(n)-a*x(n)^2
%y(n+1)=b*x(n)
x2=1+y1-a*x1.*x1;
y2=b*x1;
end
3 庞加莱截面
3.1 绘制思路
对于一个混沌系统,其轨线往往是混乱无序的,很难去简洁的描述。那么其中一个思路就是,简化信息,降低描述的维度,把空间的轨线化简为一系列离散点。
对于一个周期或拟周期运动的系统,在相空间的运动表现为一圈又一圈的转动。我们定义一个截面(一般是平面),当轨线穿过这个面时,把交点记录下来。当记录足够多的交点后,这些交点形成的图像就是庞加莱截面的图像。我们把这个和轨线相交的面称作庞加莱截面(Poincaré section)。
接下来就以杜芬(Duffing)方程分岔图的绘制大概演示一下上面所说的大概思路。
Duffing方程是以 Georg Duffing命名的一个非线性方程。它是基于强迫振动的单摆所提出的方程,它提出的时间非常早,但是被拿来做混沌研究还是比较晚的。由于它背后有着非常明显与简单的物理模型,所以甚至可以做实验去观察这个方程的非线性[6]。方程的形式为:
x ¨ = − x 3 + x − δ x ˙ + γ cos ( ω t ) \ddot{x}=-x^3+x-\delta \dot{x}+\gamma \cos{(\omega t)} x¨=−x3+x−δx˙+γcos(ωt)
把这个方程整理成一个三阶的方程组,得到:
[ x x ˙ z ] ′ = [ x ˙ − x 3 + x − δ x ˙ + γ z − ω sin ( ω t ) ] \begin{bmatrix} x \\ \dot{x} \\ z \end{bmatrix} ' =\begin{bmatrix} \dot{x} \\ -x^3+x-\delta \dot{x}+\gamma z \\ -\omega \sin{(\omega t)} \end{bmatrix} ⎣⎡xx˙z⎦⎤′=⎣⎡x˙−x3+x−δx˙+γz−ωsin(ωt)⎦⎤
这里有个随时间变化的变量cos(wt),为了方便分析,把它单独定义为z=cos(wt)。
现在,我就得到了一个三阶的非线性方程组。默认ω=1,γ=1。
之后,我们定义空间中的z=0作为其要切割轨线的平面。而且当轨线正向穿过平面时才被记录,反向穿过平面则不被记录。这是为了让一个周期只取记录1个点。
下图是当δ=1.5、δ=1.35、δ=1.15时,其三维轨线和庞加莱截面:

当然,实际上定义的z=0截面应该是空间上没有边界限制无穷大的,这里为了方便作图,所以用了一个四边形来代替,希望不要造成误解。
通过庞加莱截面,就可以知道系统的大概特性。比如当δ=1.5时,庞加莱截面是只有1个点,证明系统是周期1的系统。当δ=1.35时,庞加莱截面是变为2个点,说明系统是周期2的系统,每转两次回到起点。当δ=1.5时,庞加莱截面是变为接近一条曲线,说明系统很可能是一个准周期运动。
所以庞加莱截面的绘制方法可以分为3步:
1 计算出轨线
2 计算轨线与某一平面的交点
3 将交点绘制出来,就得到了庞加莱截面
其中第二步计算交点,通常采用插值的方法得到。
这里给出绘图代码:
%庞佳莱截面
%截面采用公式Ax+By+Cz+D=0;的形式
%采用杜芬方程
clear
clc
close all
%% 第一步,计算出轨迹
h=5e-3;
x0=0:h:1600;
y0=[0.1;0.1;1];%最后一项是cos(w*t),当t=0时必须为1.
[y1,Output]=ODE_RK4_hyh(x0,h,y0,[1.5,1,1]);
%[1.5,1,1],[1.35,1,1],[1.15,1,1]
Lx=y1(1,2000:end);
Ly=y1(2,2000:end);
Lz=y1(3,2000:end);
%% 第二步,计算与平面的交点
Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面。这里是Ax+By+Cz+D=0的形式给出的平面。
[tP_List,yP_List]=Solve_Poincare(x0,y1,Plane);%计算Poincare平面
%% 第三步,绘制庞加莱截面
%1庞加莱截面
%最开始几个点还没有稳定,没有体现出系统特点,所以放弃
figure()
plot(yP_List(1,10:end),yP_List(2,10:end),'.')%从第10个点之后开始绘制
xlim([-1,0.6])
ylim([-0.8,0.2])
%2展示用的示意图,只作为演示
figure()
hold on
patch([Lx,nan],[Ly,nan],[Lz,nan],[Lx+Ly,nan],...
'EdgeColor','interp','Marker','none','MarkerFaceColor','flat','LineWidth',0.8,'FaceAlpha',1);
plot3(yP_List(1,10:end),yP_List(2,10:end),zeros(size(yP_List(2,10:end))),...
'.','MarkerSize',8,'color','r')
patch([-1.6,0.4,0.4,-1.6],[-0.7,-0.7,0.0,0.6],[0,0,0,0],[1,1,1,1],...
'FaceAlpha',0.8,'EdgeColor',[0.5,0.5,0.5])
view([-17,39])
box on
grid on
%绘制投影的相图
set(gcf,'position',[300 200 560 500])
xlim([-2,2])
zlim([-3,1])
plot3( Lx,Ly,zeros(size(Ly))-3 ,'color','k')
hold off
%% 后置函数
function [tP_List,yP_List]=Solve_Poincare(t,y,Plane)
%截面方程z=0
% Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面
%一般只记录从负到正穿越。如果想反向也记录,可以设置Plane=-Plane。
%第二步,插值得到线与面的交点
yP_List=[];
tP_List=[];
Dis=DistancePlane(y,Plane);
N=size(y,2);
for k=1:N-1
if Dis(k)<=0 && Dis(k+1)>0
t0=t(k);t1=t(k+1);
yP0=y(:,k);yP1=y(:,k+1);
Dis0=Dis(k);Dis1=Dis(k+1);
%一维线性插值,求Dis=0时的t和y
%(相比较前面积分的4阶RK,这里用线性插值精度有点低,先这么凑合着吧)
yP=yP0+(yP1-yP0)/(Dis1-Dis0)*(0-Dis0);
tP=t0+(t1-t0)/(Dis1-Dis0)*(0-Dis0);
%储存
yP_List=[yP_List,yP];
tP_List=[tP_List,tP];
end
end
end
%点到平面的距离
function Dis=DistancePlane(xk,Plane)
% xk,坐标点,如果是3维坐标,大小就是3*N的矩阵。
% Plane,平面,形如Ax+By+Cz+D=0形式的平面。
N=size(xk,2);%计算总共多少个点
xk2=[xk;ones(1,N)];
Dis=dot(xk2,Plane*ones(1,N),1)./norm(Plane(1:end-1));
end
%两点线性插值
function y=interp2point_linear(x0,x1,y0,y1,x)
y=y0+(y1-y0)/(x1-x0)*(x-x0);
end
%两点3次插值
function y=interp2point_spline(x0,x1,y0,y1,x)
%y0包含y0的值和y0的导数,yy=y0(1),dy=y0(2)
xx0=x0;
xx1=x1;
yy0=y0(1);dy0=y0(2);
yy1=y1(1);dy1=y1(2);
cs = csape([xx0,xx1],[dy0,yy0,yy1,dy1],[1,1]);
y=ppval(cs,x);
end
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
%杜芬方程duffing,参见中国大学MOOC,北京师范大学-计算物理基础-77倒摆与杜芬方程
d=Input(1);
r=Input(2);
w=Input(3);
dy(1)=y(2);
dy(2)=-y(1)^3+y(1)-d*y(2)+r*y(3);
dy(3)=-w*sin(w*x);
F=[dy(1);dy(2);dy(3)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end
3.2 利用频闪法快速绘制
这种计算方法,具体思路还是那三步。
1 计算出轨线
2 计算轨线与某一平面的交点
3 将交点绘制出来,就得到了庞加莱截面
但是第二步不再是直接通过轨线上两点进行插值得到,而是直接通过时间t得到。
比如下面是我们3.1节的杜芬方程,我们取的是z=0平面作为庞加莱截面。
[ x x ˙ z ] ′ = [ x ˙ − x 3 + x − δ x ˙ + γ z − ω sin ( ω t ) ] \begin{bmatrix} x \\ \dot{x} \\ z \end{bmatrix} ' =\begin{bmatrix} \dot{x} \\ -x^3+x-\delta \dot{x}+\gamma z \\ -\omega \sin{(\omega t)} \end{bmatrix} ⎣⎡xx˙z⎦⎤′=⎣⎡x˙−x3+x−δx˙+γz−ωsin(ωt)⎦⎤
但是,z=0明明是可以计算出来的。z=cos(t),当t=0.5π+2kπ和t=1.5π+2kπ的时候,z无条件的等于0。
对于庞加莱截面,一个周期我们只取一个点,所以所有位于庞加莱截面上的点,其时间t都应该满足t=1.5π+2kπ。
因为,对于频闪采样法,意思就是隔一段时间取一次点,这些点天然的在某个庞加莱截面上。这种方法采用预先计算得到的时刻间隔,大大减少了程序内的计算量。
同样取δ=1.15,其庞加莱截面的结果如下图。可以看到这种偷懒方法和上一章节老老实实计算结果相同。

事实上,由于不需要再计算z具体的值,方程中甚至可以省略掉计算z的步骤。这样就变成了虽然没有z这变量,但是却依然计算了系统在z=0的庞加莱截面。
[ x x ˙ ] ′ = [ x ˙ − x 3 + x − δ x ˙ + γ cos ( ω t ) ] \begin{bmatrix} x \\ \dot{x} \\ \end{bmatrix} ' =\begin{bmatrix} \dot{x} \\ -x^3+x-\delta \dot{x}+\gamma \cos{(\omega t) } \end{bmatrix} [xx˙]′=[x˙−x3+x−δx˙+γcos(ωt)]
代码如下:
%庞佳莱截面(频闪法)
%采用杜芬方程
clear
clc
close all
%第一步,计算出轨迹
h=5e-3;
x0=0:h:1600;
y0=[0.1;0.1];%这里简化了方程,所以只有两个输入
[y1,Output]=ODE_RK4_hyh(x0,h,y0,[1.15,1,1]);
%[1.5,1,1],[1.35,1,1],[1.15,1,1],[0.1,0.35,1.4]
Lx=y1(1,:);
Ly=y1(2,:);
%Lz=cos(1*x0);
%采用频闪采样法计算
tP_Ideal=3*pi/2:(2*pi/1):x0(end);%这里考虑z=0平面,时间间隔dt=2*pi。
tP_List=zeros(1,length(tP_Ideal));
Ind_List=zeros(1,length(tP_Ideal));
for k=1:length(tP_Ideal)
[~,Ind]=min(abs( tP_Ideal(k)-x0 ));%直接根据索引来找到对应的点
Ind_List(k)=Ind;
tP_List(k)=x0(Ind);
end
yP_List=y1(:,Ind_List);
%注,如果上面时间间隔h为pi/600之类的形式,这里连min函数都可以取消,直接按照索引去寻找就行
%绘图
%1庞加莱截面
%最开始几个点还没有稳定,没有体现出系统特点,所以放弃
figure()
plot(yP_List(1,10:end),yP_List(2,10:end),'.')
xlim([-1,0.6])
ylim([-0.8,0.2])
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
d=Input(1);
r=Input(2);
w=Input(3);
dy(1)=y(2);
dy(2)=-y(1)^3+y(1)-d*y(2)+r*cos(w*x);
% dy(3)=-w*sin(w*x);%由于无需计算具体的z值,所以这里把z合并到了dy(2)项里,减少计算量
F=[dy(1);dy(2)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end
这种方法只在某些特殊的存在明确周期性的系统中才可以用的到。
当[δ,γ,ω] = [ 0.1 ,0.35 ,1.4]时,系统会由于混沌,其庞加莱截面还会出现混沌形式:
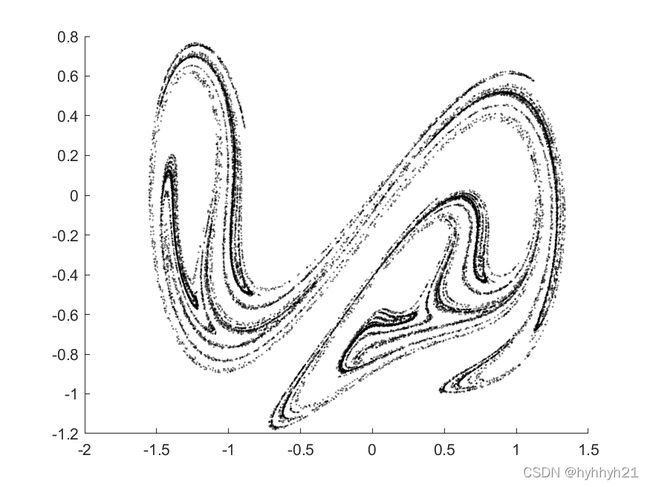
上面的图涉及到的点非常多,所以无法一口气全部得到,只能采取一段一段计算的方式得到。绘图代码如下,仅供参考:
clear
clc
close all
%初始化
h=2*pi/700;
x0=0:h:2e5*pi/700;
y0=[0.1;0.1];%最后一项是cos(w*t),当t=0时必须为1
%这里一口气求出一大堆点不太现实,内存有限,所以采取分批计算,逐步绘图来实现
figure(1)
hold on
for k=1:100
[y1,Output]=ODE_RK4_hyh(x0,h,y0,[0.1,0.35,1.4]);
Lx=y1(1,:);
Ly=y1(2,:);
%采用频闪采样法计算
%由于w变为了1.4,这里还是z=0平面,采样间隔改为 (3*pi/2:(2*pi/1):2000)/1.4
yP_List=y1(:,376:500:end);%注,这里376=3/2/1.4*350+1
%内存有点不够了,分段进行下面的计算
x0=x0+2e5*pi/700;%时间整体向后移动
y0=y1(:,end);%把最后一刻的状态当做下一个时间段初始状态
%绘图
%1庞加莱截面
scatter(yP_List(1,1:end),yP_List(2,1:end),0.8,'k','MarkerEdgeAlpha',0.6)
%disp(k)
end
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
d=Input(1);
r=Input(2);
w=Input(3);
dy(1)=y(2);
dy(2)=-y(1)^3+y(1)-d*y(2)+r*cos(w*x);
F=[dy(1);dy(2)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end
4 非线性系统的分岔图
前面介绍了离散系统绘制分岔图。对于连续系统,如何绘制分岔图呢?
大概思路为:
1先绘制出系统的轨线 (3维系统转3维曲线,用轨线)
2绘制轨线和某个面的交点(3维曲线转2维点,用庞加莱截面)
得到某个平面的上的若干点后,问题就转化为前面二维离散系统的分岔图了:
4将这些点投影到某个线上(2维的点转1维的值)
5绘制分岔图
目的就是把连续系统转化为可以绘制分岔图的散点形式。
4.1 Duffing系统分岔图
以前面的介绍的杜芬方程为例,固定ω=1,γ=1,改变δ的分岔图如下。绘制方法就是计算出每一个δ下的庞加莱截面,然后仿照前面离散点分岔的,取坐标y作为分岔图。
绘图代码如下,计算时间比较长,需要耐心等待一段时间:
%利用庞佳莱截面绘制分岔图
clear
clc
close all
%第一步,计算出轨迹
h=8e-3;
x0=0:h:1600;
y0=[0.1;0.1];%最后一项是cos(w*t),当t=0时必须为1.
%不同的d
d=0.5:0.002:1.5;%0.02
N_c=length(d);
N_P=250;%假设穿过截面的共有250个点
BF=nan(N_c,N_P);
%第二步,这里直接用频闪法求出截面所在点的索引
%z=0平面
tP_Ideal=3*pi/2:(2*pi/1):x0(end);%这里考虑z=0平面,时间间隔dt=2*pi。
tP_List=zeros(1,length(tP_Ideal));
Ind_List=zeros(1,length(tP_Ideal));
for m=1:length(tP_Ideal)
[~,Ind]=min(abs( tP_Ideal(m)-x0 ));
Ind_List(m)=Ind;
tP_List(m)=x0(Ind);
end
%第三步,开始对每一个d进行循环,计算其庞加莱截面
for k=1:N_c
d_k=d(k);
[y1,~]=ODE_RK4_hyh(x0,h,y0,[d_k,1,1]);
yP_List=y1(:,Ind_List);
%储存
N_P_temp=size(tP_List,2);
if N_P_temp>N_P
BF(k,1:N_P)=yP_List(2,1:N_P);%取坐标y作为分岔图
else
BF(k,1:N_P_temp)=yP_List(2,1:N_P_temp);%取坐标y作为分岔图
end
disp(d_k)
end
%最后一步,绘图
figure()
hold on
for k=1:N_c
d_k=d(k);
plot(d_k*ones(1,N_P-30+1),BF(k,30:N_P),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
d=Input(1);
r=Input(2);
w=Input(3);
dy(1)=y(2);
dy(2)=-y(1)^3+y(1)-d*y(2)+r*cos(w*x);
F=[dy(1);dy(2)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end
4.2 Rossler系统分岔图
Rossler系统是Rössler本人在70年代提出的一个非线性系统,形式比较简单,但是却依然拥有复杂的非线性行为。
方程为:
x ˙ = − y − z y ˙ = x + a y z ˙ = b + z ( x − c ) \dot{x}=-y-z \\ \dot{y}=x+ay \\ \dot{z}=b+z(x-c) \\ x˙=−y−zy˙=x+ayz˙=b+z(x−c)
下图绘制了a=0.1,b=0.1,改变不同的c绘制的轨迹图。

这里根据其轨迹特性,选择x=0.1平面作为其庞加莱截面。
绘图代码如下,运行时间比较长,还需耐心等待。
%利用庞佳莱截面绘制分岔图
%截面采用公式Ax+By+Cz+D=0;的形式
%Rossler方程
clear
clc
close all
h=5e-3;%时间步长
x0=0:h:800;%时间
y0=[2;2;2];
%不同的c开始循环
c=3:0.02:16;
N_c=length(c);
N_P=300;%假设穿过截面的共有300个点
BF=nan(N_c,N_P);
for k=1:N_c
c_k=c(k);disp(c_k)
%计算出轨迹
[y1,~]=ODE_RK4_hyh(x0,h,y0,[0.1,0.1,c_k]);
%计算Poincare平面
Plane=[1;0;0;0.1];%x=0.1平面(正方向)
[tP_List,yP_List]=Solve_Poincare(x0,y1,Plane);%计算Poincare平面
%储存y值作为待会分岔图的点
N_P_temp=size(tP_List,2);
if N_P_temp>N_P
BF(k,1:N_P)=yP_List(2,1:N_P);
else
BF(k,1:N_P_temp)=yP_List(2,1:N_P_temp);
end
end
%绘制分岔图
figure()
hold on
for k=1:N_c
c_k=c(k);
plot(c_k*ones(1,N_P-30+1),BF(k,30:N_P),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
%后置函数
function [tP_List,yP_List]=Solve_Poincare(t,y,Plane)
%截面方程z=0
% Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面
%一般只记录从负到正穿越。如果想反向也记录,可以设置Plane=-Plane。
%第二步,插值得到线与面的交点
yP_List=[];
tP_List=[];
Dis=DistancePlane(y,Plane);
N=size(y,2);
for k=1:N-1
if Dis(k)<=0 && Dis(k+1)>0
t0=t(k);t1=t(k+1);
yP0=y(:,k);yP1=y(:,k+1);
Dis0=Dis(k);Dis1=Dis(k+1);
%一维线性插值,求Dis=0时的t和y
%(相比较前面积分的4阶RK,这里用线性插值精度有点低)
yP=yP0+(yP1-yP0)/(Dis1-Dis0)*(0-Dis0);
tP=t0+(t1-t0)/(Dis1-Dis0)*(0-Dis0);
%储存
yP_List=[yP_List,yP];
tP_List=[tP_List,tP];
end
end
end
%点到平面的距离
function Dis=DistancePlane(xk,Plane)
% xk,坐标点,如果是3维坐标,大小就是3*N的矩阵。
% Plane,平面,形如Ax+By+Cz+D=0形式的平面。
N=size(xk,2);%计算总共多少个点
xk2=[xk;ones(1,N)];
Dis=dot(xk2,Plane*ones(1,N),1)./norm(Plane(1:end-1));
end
%两点线性插值
function y=interp2point_linear(x0,x1,y0,y1,x)
y=y0+(y1-y0)/(x1-x0)*(x-x0);
end
%两点3次插值
function y=interp2point_spline(x0,x1,y0,y1,x)
%y0包含y0的值和y0的导数,yy=y0(1),dy=y0(2)
xx0=x0;
xx1=x1;
yy0=y0(1);dy0=y0(2);
yy1=y1(1);dy1=y1(2);
cs = csape([xx0,xx1],[dy0,yy0,yy1,dy1],[1,1]);
y=ppval(cs,x);
end
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
%Rossler 吸引子
a=Input(1);
b=Input(2);
c=Input(3);
dy(1)=-y(2)-y(3);
dy(2)=y(1)+a*y(2);
dy(3)=b+y(3)*(y(1)-c);
F=[dy(1);dy(2);dy(3)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end
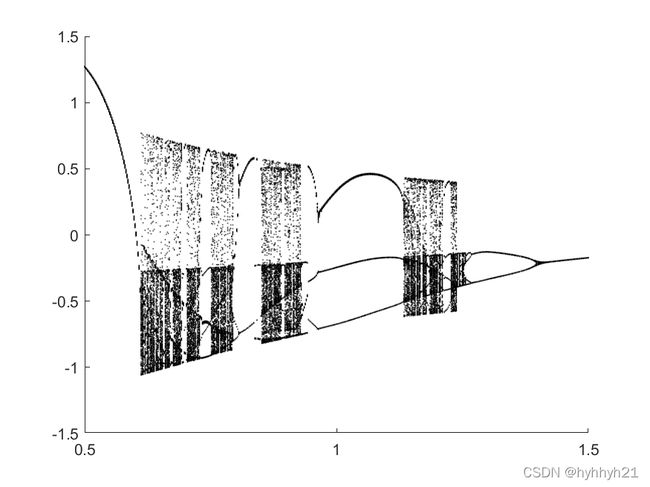
分岔图绘制如下:

庞加莱截面的选取会导致系统分岔图的形状发生改变。但是不会改变分岔点的位置。因为分岔点的位置是由系统本身所决定。
4.3 Lorenz系统分岔图
Lorenz系统是气象学家洛伦兹发现并提出的一个非线性系统,也是混沌学科的开端。在模拟大气流动时,洛伦兹发现初始的一个小小的误差,都会导致系统未来极大的变化。这种思想在20世纪60年代,给了那些物理学界中决定论者沉重的打击。洛伦兹也将这种不确定性,总结为“蝴蝶效应”。
这个系统可以被写为:
x ˙ = a ( y − x ) y ˙ = r x − y − x z z ˙ = x y − b z \dot{x}=a(y-x)\\ \dot{y}=rx-y-xz\\ \dot{z}=xy-bz x˙=a(y−x)y˙=rx−y−xzz˙=xy−bz
一般系统a=10,b=8/3,变化r值来观察系统的不同样子。下图分别展示了取不同r值所对应的xy平面的三维相轨线图:
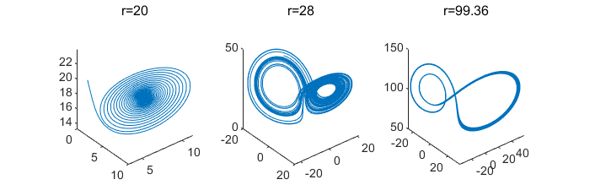
分岔图为:

绘图代码如下:
%利用庞佳莱截面绘制分岔图
%截面采用公式Ax+By+Cz+D=0;的形式
%Lorenz方程
clear
clc
close all
h=2e-3;
x1=100;
x0=0:h:x1;
y0=[2;2;2];
%不同的c
c=1:1:500;
N_c=length(c);
N_P=300;%假设穿过截面的共有300个点
BF=nan(N_c,N_P);
for k=1:N_c
c_k=c(k);disp(c_k)
%计算出轨迹
[y1,~]=ODE_RK4_hyh(0:10*h:x1,10*h,y0,[10,8/3,c_k]);%先粗略的计算前几步,然后排除初始点的影响,舍弃不要
[y1,~]=ODE_RK4_hyh(x0+x1,h,y1(:,end),[10,8/3,c_k]);
%计算Poincare平面
Plane=[1;-1;0;0];%x-y=0平面(正方向)
[tP_List,yP_List]=Solve_Poincare(x0,y1,Plane);%计算Poincare平面
%对于Lorenz系统再加一条,如果系统稳定了,则将稳定点也记录在最终分岔图内:
if isempty(tP_List) && sum(y1(1,end)-y1(2,end))<1e-2%如果最后x和y足够接近,则认为收敛了
tP_List=x0(end-1:end);
yP_List=y1(:,end-1:end);
end
%储存y值作为待会分岔图的点
N_P_temp=size(tP_List,2);
if N_P_temp>N_P
BF(k,1:N_P)=yP_List(2,1:N_P);
else
BF(k,1:N_P_temp)=yP_List(2,1:N_P_temp);
end
end
%绘制分岔图
figure()
hold on
for k=1:N_P
c_k=c(k);
plot(c_k*ones(1,N_P),BF(k,1:N_P),...
'LineStyle','none','Marker','.','MarkerFaceColor','k','MarkerEdgeColor','k',...
'MarkerSize',1)
end
hold off
function [tP_List,yP_List]=Solve_Poincare(t,y,Plane)
%截面方程z=0
% Plane=[0;0;1;0];%一般情况下是个垂直某个轴的平面
%一般只记录从负到正穿越。如果想反向也记录,可以设置Plane=-Plane。
%第二步,插值得到线与面的交点
yP_List=[];
tP_List=[];
Dis=DistancePlane(y,Plane);
N=size(y,2);
for k=1:N-1
if Dis(k)<=0 && Dis(k+1)>0
t0=t(k);t1=t(k+1);
yP0=y(:,k);yP1=y(:,k+1);
Dis0=Dis(k);Dis1=Dis(k+1);
%一维线性插值,求Dis=0时的t和y
%(相比较前面积分的4阶RK,这里用线性插值精度有点低)
yP=yP0+(yP1-yP0)/(Dis1-Dis0)*(0-Dis0);
tP=t0+(t1-t0)/(Dis1-Dis0)*(0-Dis0);
%储存
yP_List=[yP_List,yP];
tP_List=[tP_List,tP];
end
end
end
%点到平面的距离
function Dis=DistancePlane(xk,Plane)
% xk,坐标点,如果是3维坐标,大小就是3*N的矩阵。
% Plane,平面,形如Ax+By+Cz+D=0形式的平面。
N=size(xk,2);%计算总共多少个点
xk2=[xk;ones(1,N)];
Dis=dot(xk2,Plane*ones(1,N),1)./norm(Plane(1:end-1));
end
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程,参见数值分析求解常系数微分方程相关知识
%高次用列向量表示,F=[dy(1);dy(2)];y(1)为函数,y(2)为函数导数
%Lorenz 吸引子
a=Input(1);b=Input(2);r=Input(3);
dy(1)=a*(y(2)-y(1));
dy(2)=r*y(1)-y(2)-y(1)*y(3);
dy(3)=y(1)*y(2)-b*y(3);
F=[dy(1);dy(2);dy(3)];
Output=[];
end
function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
yn=y(:,ii);
xn=x(ii);
[K1,~]=Fdydx(xn ,yn ,Input);
[K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
[K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
[K4,~]=Fdydx(xn+h ,yn+h*K3 ,Input);
y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end