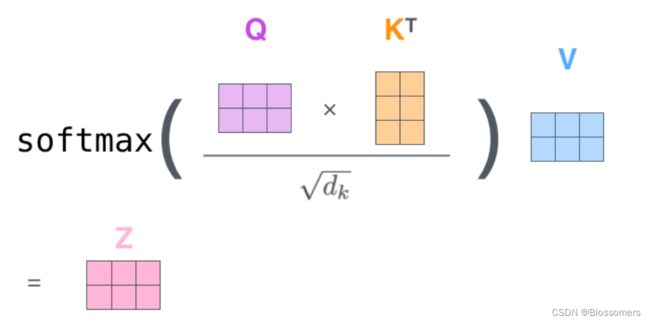Self-attention模块学习记录（附代码复现）

尝试一下以问答的形式，阐述自己对自注意力模型的理解。

1、self-attention模块，输入与输出在通道数上是相同的，如何理解？

这是由模块的计算方式所决定的。

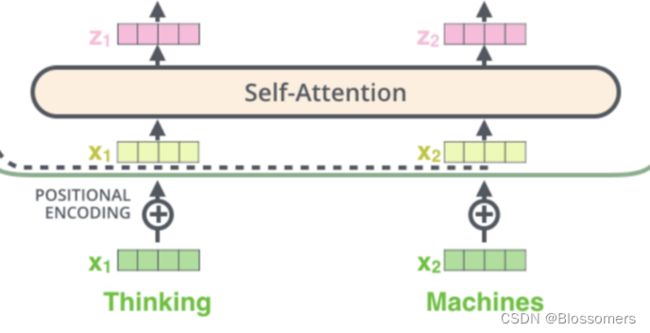
首先需要弄清楚的是，模块的输入可以看作是一个句子里的各个词组，比如说I love eating apples. 那输入就包括这四个单词，以及句子的结束标志'.' 经过embedding得到的特征向量。输出的是这个词组与其他词组的关联程度，也就是Z向量。从直观上看，这两者都是围绕着“一个词”所做的编码工作，那么在通道数目上自然是会相等的。

Q、K、V矩阵的运算方式如下图：

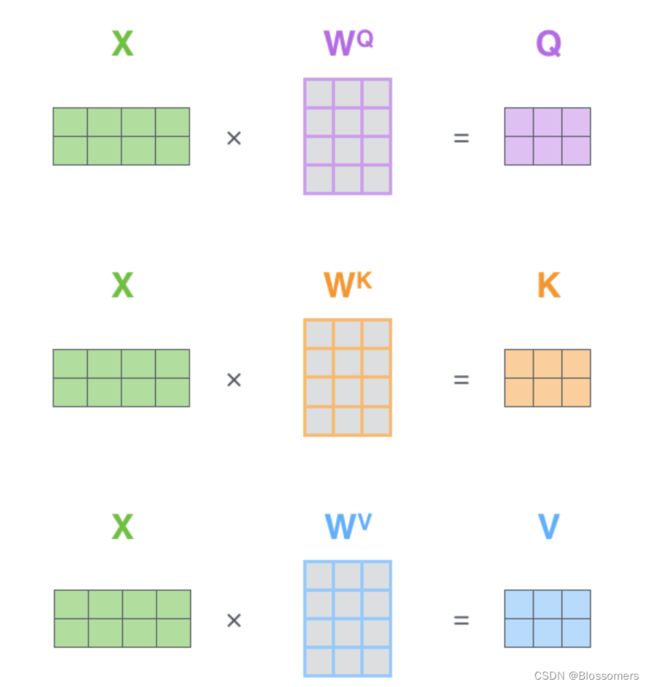
其中Q、K、V矩阵正是网络需要训练的参数。它们由输入X分别与、、相乘得到。

2、如何理解Multi-head的作用？

受到李沐老师的启发，我认为Multi-head与CNN中多通道的卷积层发挥的作用是类似的，是去帮助网络能够有能力识别不同的模式，增加其学习能力。具体来说，可以帮助网络关注到每一个位置上的词，而不是被自己当前位置这个词组占据了绝大部分的注意力。

具体应用来说，如果我们给了一个Eight-head的self-attention模块，那么一个输入vector就会对应8个Zvector的输出。这个时候再把八个vector concat起来，与新的矩阵做乘法，最终可以得到一个新的输出vectorZ。

这也符合self-attention引入的初衷：根据一个sequence内别的语句的词义 来更好地解码当前这个  词的含义。

问题：原文为什么会说这样的Multi-Head并不影响计算复杂度呢？这个维度降低到底是啥意思

或许应该去代码里找一下答案。 （Mark一下 搞明白了回来再记录）

3、为何Softmax之前需要对于做归一化?

因为这样可以产生更加稳定的梯度信息。Softmax本身对于输出较大的值，就会让其在输出概率占比中占的更大。而网络的训练目的就是要让对应值的概率接近于1。如果一开始值就非常大的话，对于softmax来说就没有什么梯度可言，这会导致网络难以训练下去。

至于为什么是除以，我的理解是因为softmax的值正是由Q与K做dotproduct而得到的。这样就可以动态地根据KVector的长度，调整输入softmax的值。

4、对于位置编码Positional-encoding的理解？

位置编码是加在最开始的embedding的Xvector上的，与Xvector同维度。

这是为了更好地表征sequence里不同词之间的次序关系

具体的编码规则感觉比较随意，只要能表征出词与词之间的距离信息就够了。在论文中作者用的是半边sin+半边cos的组合，这种组合仅基于当前的位置和sequence的总长度，所以可以推广到训练集里不曾出现过的长度词上。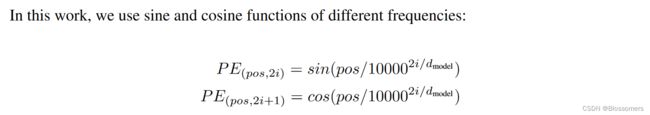

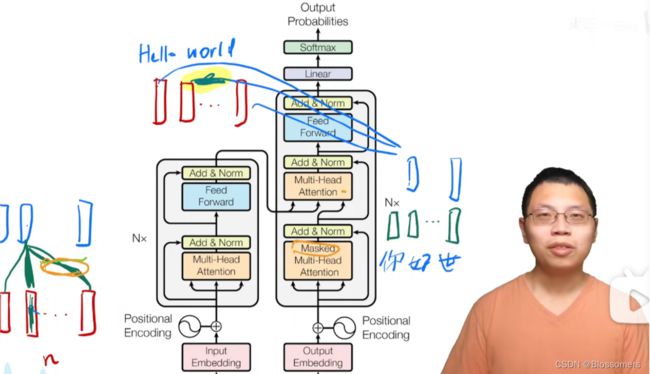
5、如何理解encoder-decoder self-attention layer？

以李沐老师的讲解，可以看出：这一层的attention就是为了让decoder里的词组去“注意到”encoder的输入，比如让“你”注意到“Hello”，从而建立起两者之间的联系。

这里的具体实现方式是，把decoder输出作为Q，encoder的输出作为K，V，放入这个attention layer里进行计算。

顺带一提，在decoder的“Masked Multi-head Attention”模块里，Masked存在的意义是让，当前解码的词只与前面已经解码的词去做attention，不能够与还未出现的词去做。这符合自回归的逻辑(self-regressive）。

下面是代码复现环节

1、实现一个self-attention模块（numpy version）

import numpy as np
from numpy.random import randn

n = 32 # sequence里有32个词
d = 256 # 256维特征

x = randn(d,n)
w = [randn(d,d) for i in range(3)] # 构建wq,wk,wv矩阵
q,k,v = [wi@x for wi in w]

def softmax(x):
    e_x = np.exp(x-np.max(x))# 防溢出
    return e_x/e_x.sum(axis=0)

out = v @ softmax(k.T @ q)/d**(0.5)

print(out.shape)

可以看到x与output的维度是保持一致的（在dim=1上保持一致其实就行了，这对应一个个词）

Pytorch Version

from math import sqrt
import torch
import torch.nn as nn


# Self-Attention 机制的实现
class Self_Attention(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self,input_dim,dim_k,dim_v):
        super(Self_Attention,self).__init__()
        self.q = nn.Linear(input_dim,dim_k) # (4,3,input_dim) -> (4,3,dim_k)
        self.k = nn.Linear(input_dim,dim_k) # 
        self.v = nn.Linear(input_dim,dim_v)
        self._norm_fact = 1 / sqrt(dim_k)
        
    
    def forward(self,x):
        Q = self.q(x) # Q: batch_size * seq_len * dim_k
        K = self.k(x) # K: batch_size * seq_len * dim_k
        V = self.v(x) # V: batch_size * seq_len * dim_v

        atten = nn.Softmax(dim=-1)(torch.bmm(Q,K.permute(0,2,1))) * self._norm_fact # Q * K.T() # batch_size * seq_len * seq_len
        
        output = torch.bmm(atten,V) # Q * K.T() * V # batch_size * seq_len * dim_v
        
        return output



X = torch.randn(4,3,2)
self_attention = Self_Attention(2,4,5)
res = self_attention(X)

Reference：

强烈推荐！！讲的太好了这篇，可视化做的相当好

Self-Attention概念详解_fkyyly的博客-CSDN博客_self-attention

【手撕Self-Attention】self-Attention的numpy实现和pytorch实现_顾道长生'的博客-CSDN博客