基于用户的协同过滤推荐算法研究

摘要：近年来，随着线上可供选择的增加，推荐系统变得越来越不可或缺。推荐系统通过发掘用户的行为，找到用户的个性化需求，从而将长尾物品准确推荐给需要它的用户，帮助用户找到他们感兴趣但很难发现的物品。本文采用基于用户的协同过滤算法实现电影的推荐，并针对该方法存在的稀疏性，冷启动和扩展性问题进行了分析，结果表示此算法可以得到不错的推荐效果。
关键词：协同过滤；用户；皮尔逊系数；相似度
Abstract：In recent years, with the increase of online choices, recommendation system becomes more and more indispensable. Recommendation system finds users’ personalized needs by exploring users’ behavior, and accurately recommending long tail items to users who need them which could helps users to find items they are interested in but difficult to find. In this paper, user-based collaborative filtering algorithm is used to implement movie recommendation, and the sparsity, cold start and expansibility of this method are analyzed. The results show that this algorithm can get good recommendation effect.
Key words: collaborative filtering; users; Pearson coefficient; similarity

一．推荐系统介绍
随着电子商务和网络通讯的兴起,互联网成为人们获取信息以及购物的重要工具,导致了数据的爆炸式增长,也就是信息过载。用户要从互联网上的茫茫信息海洋中找到自己需要的信息十分困难,因此,推荐系统应运而生。推荐系统的目标是帮助用户从大量的物品中筛选出最适合其偏好的个性化物品，除此之外，许多商业公司将推荐系统运用到了实际中，通过推按物品来确定他们的目标用户。多年来，用于推荐系统的不同算法已得到了发展。高质量的推荐系统会使用户对系统产生依赖，因此，推荐系统不仅能为用户提供个性化服务，还能与用户建立长期稳定的关系，提高用户忠诚度，防止用户流失。通用的推荐系统模型流程为
a）推荐系统通过用户行为，建立用户模型；
b）通过物品的信息，建立推荐对象模型；
c）通过用户兴趣匹配物品的特征信息，再经过推荐算法计算筛选，找到用户可能感兴趣的推荐对象，然后推荐给用户。
用户行为数据在网站上最简单的存在形式就是日志，日志中记录了用户的各种行为，比如网页浏览、点击、购买、评论、评分等等。用户行为在个性化推荐系统中一般分为显性反馈行为和隐性反馈行为。显性反馈行为包括用户明确表示对物品的喜好的行为，比如给物品评分，而隐性反馈行为是指那些不能明确反应用户喜好的行为，比如页面浏览行为。隐性反馈数据比显性反馈不明确，但其数据量更庞大。
二．数据预处理
2.1 相似度计算
相似度计算主要有三个经典算法：余弦定理相似性度量、欧氏距离相似度度量和皮尔逊相关系数法
（1）余弦定理相似性度量
通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。在比较过程中，向量的规模大小不予考虑，仅仅考虑到向量的指向方向。余弦相似度通常用于两个向量的夹角小于90°之内，因此余弦相似度的值为0到1之间。

（2）欧氏距离相似性度量
与余弦定理通过方向度量相似度不同，欧氏距离是通过计算样本实际距离在度量相似度的。二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离

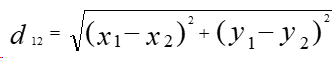
（3）皮尔逊相关系数
两个变量之间的相关系数越高，从一个变量去预测另一个变量的精确度就越高，这是因为相关系数越高，就意味着这两个变量的共变部分越多，所以从其中一个变量的变化就可越多地获知另一个变量的变化。如果两个变量之间的相关系数为1或-1，那么你完全可由变量X去获知变量Y的值。
当相关系数为0时，X和Y两变量无关系；当相关系数在0.00与1.00之间，X、Y正相关关系；当相关系数在-1.00与0.00之间，X、Y负相关关系。由此可知，相关系数的绝对值越大，相关性越强，相关系数越接近于1和-1，相关度越强，相关系数越接近于0，相关度越弱。
2.2 抽样
抽样是数据挖掘从大数据集中选择相关子数据集的主要技术，用于数据预处理和最后的解释步骤中。抽样的原因是处理全部数据集的计算开销太大，同时可以被用来创造训练和测试数据集。其中，训练集被用于分析阶段学习参数或配置算法，测试及用于评估训练阶段获得的样本或模型，确保将来在未知数据上运行良好。
抽样的关键是发现具有整个原始数据及代表性的子集。最简单的抽样技术是随机抽样。抽样可能导致过特殊化划分的训练集和测试集，因此训练的过程可以重复好几次。在分离训练集和测试集是最常用的是使用80/20的训练集和测试集比例，并使用无替代的标准随机抽样。
在推荐系统中常用的方法是从用户中抽取可能的反馈以用户评分的方式来划分训练和测试。交叉验证的方法也很常见。在一般案例中可接受标准随机抽样，但在其他场景中需要用不同的方法定向调整抽样出来的测试集。
2.3 降维
推荐系统中不仅有定义高维空间的数据集，而且在空间中的信息非常稀疏。例如，每个对象只有几个有限的特征有值。密度以及点之间的距离，这些对于聚类和孤立点检测非常重要，但在高维空间中的意义并不大，这就是著名的维度灾难。降维技术通过把原始高维空间转化成低维有助于克服这类问题。
推荐系统中最常用的降维算法有：主成分分析（PCA）和奇异值分解（SVD）。主成分分析（PCA）是一种经典统计方法，主成分分析可以获得一组有序的成分列表，根据其最小平方误差计算出变化最大的值。列表中第一个成分所代表的变化量要比第二个成分所代表的变化量大，以此类推，我们可以通过忽略这些对变化贡献较小的成分来降低维度。
2.4 去燥
数据挖掘中采集的数据可能有各种噪声，如缺失数据，或者是异常数据。去燥是非常重要的预处理步骤，其目的是在最大化信息量时去除不必要的影响。一般意义上，我们把噪声定义为在数据收集阶段收集到的一些可能影响数据分析和解释结果的伪造数据。 在推荐系统环境中，我们区分自然的和恶意的噪声。前者是用户在选择偏好反馈时无意识产生的，后者是为了偏离结果在系统中故意引用的。为了解决这个问题，我们可以设计去燥的方法，能够通过要求用户重新评价一些物品来提高精确度。我们推断通过预处理步骤来提高精确度能够比复杂的优化算法优化效果好得多。
三．协同过滤算法
3.1 基于用户的协同过滤（user-based）
这种算法给用户推荐和他兴趣相似的其他用户喜欢的物品。算法步骤：(1) 找到和目标用户兴趣相似的用户集合；(2) 找到这个集合中的用户喜欢的，且目标用户没有听说过的物品，推荐给目标用户。算法的关键是计算两个用户的兴趣相似度。协同过滤计算用户兴趣相似度是利用用户行为的相似度。
3.2 基于物品的协同过滤（item-based）
这种算法给用户推荐和他之前喜欢的物品相似的物品。该算法是目前业界应用最多的算法，如亚马逊、Netflix、YouTube，都是以该算法为基础。算法步骤：(1) 根据用户的历史行为，计算物品之间的相似度；(2) 根据物品的相似度和用户的历史行为给用户生成推荐列表。两个物品产生相似度，是因为它们共同被很多用户喜欢，也就是说，每个用户都可以通过它们的历史兴趣列表给物品“贡献”相似度。
3.3 关联算法
3.3.1 关键指标
一般我们可以通过找出用户购买的所有物品数据里频繁出现的项集活序列，来做频繁集挖掘，找到满足支持度阈值的关联物品的频繁N项集或者序列。如果用户购买了频繁N项集或者序列里的部分物品，那么我们可以将频繁项集或序列里的其他物品按一定的评分准则推荐给用户，这个评分准则包括支持度，置信度和提升度等。常用的关联推荐算法有Apriori，FP Tree和PrefixSpan。下面简要介绍三个关键指标。
支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。如果我们有两个想分析关联性的数据X和Y，则对应的支持度为:

置信度体现了一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。如果我们有两个想分析关联性的数据X和Y，X对Y的置信度为

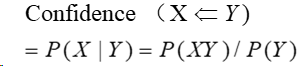
提升度表示含有Y的条件下，同时含有X的概率，与X总体发生的概率之比，即:

提升度体先了X和Y之间的关联关系, 提升度大于1则X⇐YX⇐Y是有效的强关联规则，提升度小于等于1则X⇐YX⇐Y是无效的强关联规则。
3.3.2 算法简介
Apriori算法是常用的用于挖掘出数据关联规则的算法，它用来找出数据值中频繁出现的数据集合，以此辅助人们做出决策。一般来说，要选择一个数据集合中的频繁数据集，则需要自定义评估标准。最常用的评估标准是用自定义的支持度，或者是自定义支持度和置信度的一个组合。对于Apriori算法，我们使用支持度来作为我们判断频繁项集的标准。而Apriori算法的目标是找到最大的K项频繁集。这要求我们要找到符合支持度标准的频繁集，并且要找到最大个数的频繁集，主要方法是迭代。由于它需要多次扫描数据，I/O成为很大的瓶颈，为了解决这个问题，FP Tree算法（也称FP Growth算法）进行了优化。通过引入项表头，FP Tree和节点链表三个数据结构，使得只需要扫描两次数据集，因此提高了算法运行的效率。
3.4 分类算法
根据用户评分的高低，将分数分段就可以把问题变成分类问题。目前使用最广泛的是逻辑回归，其广泛应用于大型公司，由于我们可以对每个物品是否推荐给出一个明确的概率，因此可以对数据的特征做工程化，进而调优。常见的分类推荐算法有逻辑回归和朴素贝叶斯。逻辑回归由线性回归发展来，对于线性回归模型，可以得到输出特征向量Y和输入样本矩阵X之间的线性关系，利用函数将Y转化为g(Y)（常用sigmoid函数），可以得到只有两种结果的逻辑回归,从而达到分类的效果。在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。对于大多数的分类算法，都是直接学习出特征输出Y和特征X之间的关系，比如决策树,KNN,逻辑回归，支持向量机等都是判别方法。但是朴素贝叶斯通过直接找出特征输出Y和特征X的联合分布P(X,Y)的一种生成方法。
四．代码实现与结果展示
本文实现基于用户的协同过滤推荐算法。用到的数据结构有数组和矩阵。利用皮尔逊相关系数来计算用户间相似度，通过设定合适的min_periods参数值实现较为准确地电影推荐。
4.1 数据规整
使用的数据分析包为pandas，Numpy和matplotlib，数据集为经典数据集ml-100k。首先将评分数据从ratings.dat中读出到一个DataFrame 里，然后 取出user_id、movie_id 和 rating的数值放到一个以 user 为行，movie 为列，rating 为值的data表里。

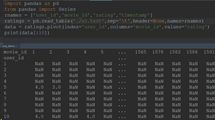
可以看到这个表相当得稀疏，填充率大约只有 5%，接下来要实现推荐的第一步是计算 user 之间的相关系数。
4.2相关度测算
DataFrame计算用户相似度可通过.corr(method=‘pearson’, min_periods=1) 方法，对所有列互相计算相关系数。其中method默认为皮尔逊相关系数，min_periods参数的作用是设定计算相关系数时的最小样本量，低于此值的一对列将不进行运算。这个值的取舍关系到相关系数计算的准确性，因此接下来确定具体的参数值。
4.3 min_periods 参数测定
统计在 min_periods 取不同值时，相关系数的标准差值（越小越好）但同时需要考虑到样本空间稀疏的问题，min_periods 定得太高会导致滤除后的数据太小，因此需要选定一个折中的值。
这里我们测定评分系统标准差的方法为：在data中挑选一对重叠评分最多的用户，用他们之间的相关系数的标准差去对整体标准差做点估计。在此前提下对这一对用户在不同样本量下的相关系数进行统计，观察其标准差变化。
首先，要找出重叠评分最多的一对用户。计算出其相似度为0.37左右。

对这两个用户的相关系数统计，我们分别随机抽取 5,10,15,20,30 个样本值，各抽 20 次。并统计结果：

观察stu一行，我们需要得到较低的方差，但参数值不能设置太高（以防滤除后的数据量过少），因此我们取参数为10。
4.3 min_periods 参数检验
通过算法检验，进一步判断min_periods 参数的设置是否合理。随机抽取300个用户，每人随机提取一个评价另存到一个数组里，并在数据表中删除这个评价。然后基于阉割过的数据表计算被提取出的评分的期望值，最后与真实评价数组进行相关性比较，看结果如何。接下来对与用户相关系数大于 0.1 的其他用户评分进行加权平均，权值为相关系数。

我们可以看到，当参数设置为10时，在随机抽取的300个用户中，依然有119个被滤除，但同时得到了0.57的相关系数。证明参数设置为10比较合理。
4.5 实现推荐

五．面临问题
尽管协同过滤技术自被提出以来，得到了推广和应用，也取得了很大的成功，但是由于自身的算法特性以及应用场景不可回避的一些问题，该方法也面临着一系列挑战，主要表现在：
5.1 稀疏性问题（Sparsity）
在没有任何刺激和鼓励评分的优惠措施下，用户自愿给出评价的很少，更不用说不同用户在同一项目上的共同评价了。传统协同过滤推荐算法在评价数据稀疏的情况下，用户间、项目间的相似性计算不准确，导致推荐精度受到极大的影响。
5.2 冷启动问题（Cold-start）
推荐系统需要根据用户的历史评价数据预测用户未来的兴趣，当一个新用户或一个新项目进入系统，亦或是一个全新的系统刚启动，都会面临冷启动问题。
5.3 扩展性问题（Scalability）
正常的商业网站都会存在数以万计的用户和项目，推荐算法在最近邻居计算时的搜索时间和空间将会非常庞大。可想而知，在如此巨大的数据量面前，协同过滤推荐方法很难保证算法的实时性。
六．解决方案
6.1稀疏性
解决数据稀疏性的问题，主要有两种思路：其一，基于数据填充的方法，借助其他有用信息建立有效的项目特征模型和用户兴趣模型并以此弥补评价数据的稀疏问题，这类信息可以是项目的内容信息[1]、用户对项目的标签信息[2]、用户对项目的隐式反馈数据[3]等等。其二，在原有评分数据的基础上，通过矩阵划分、聚类、矩阵分解等机器学习方法进行评分数据的预处理。
针对评价数据的稀疏性问题，文献[4]基于降低维度的思想，将参与相似度计算的两个用户投影到一个低维空间上，增加评价数据的稠密度，从而提高了协同过滤算法的效率。文献[5]提出了基于Bayesian模型的多准则推荐算法，该方法从多方面建立用户偏好数据，并通过隐主题将用户和项目映射到各自群体，实验证明贝叶斯模型在多准则评价推荐系统中是有效的，同时可以缓解冷启动问题。文献[6]为了降低数据的稀疏度，对原有评分矩阵进行划分，尽可能缩小近邻搜索的范围和需要预测的资源数目，实验结果表明该方法在算法性能上优于传统协同过滤算法。
6.2冷启动
目前针对冷启动问题提出了一些解决方法，如随机推荐法（对于新用户，系统从包括新项目在内的所有项目中随机选取进行推荐，然后根据用户的评价反馈，了解新用户的兴趣偏好同时得到接受新项目的用户群体）、平均值法（将项目的评分均值作为目标用户对未评价项目的预测值）、众数法（将用户曾经使用过最多的评价值作为对未评价项目的预测值）。另一类方法是，在计算相似性时融入用户的人口统计学信息[7]、背景知识（社交网络[8]）、信任关系[9]，综合考虑项目的内容信息[10]等。不同的算法具有各自的优缺点，具有一定的适用场景。
6.3扩展性
协同过滤推荐算法的时间复杂度为O(n2m)，当推荐系统面临数以百万甚至千万级别的用户和项目时，计算开销非常庞大，算法的实时性将很难保证，相应的推荐系统将面临算法的扩展性问题。一类方法是采用并行技术，以提高算法的运行效率[11]。比如，文献[12]提出了一种基于扩展向量的并行协同过滤推荐模型，为了解决冷启动问题和向目标用户提供更准确的推荐结果，文中对项目向量进行了扩展，并运用并行计算框架对系统进行了进一步的优化。与传统的协同过滤推荐方法相比，该方法不仅克服了冷启动问题，提高了一倍的推荐精度，而且在理想环境下可以提高170倍运行速度。
另一类方法是采用降维、聚类、分类等策略对评分样本数据进行离线学习，建立可以用来推荐的模型，一定程度上解决了算法的扩展性问题。例如，SVD等降维技术通过压缩矩阵，降低算法的时间复杂度，同时确保推荐结果的准确性。
七．参考文献
[1]孙金刚，艾丽蓉.基于项目属性和云填充的协同过滤推荐算法[J].计算机应用，2012,32(3):658-660.
[2]郭彩云,王会进.改进的基于标签的协同过滤算法[J].计算机工程与应用,2016,52(8):56-61.
[3]Cui H,Zhu M.Collaboration filtering recommendation optimization with user implicit feedback[J].Journal of Computational Information Systems,2014,10(14):5855-5862.
[4]Sarwar B,Karypis G,Konstan J,et al.Application of dimensionality reduction in recommender systems—A case study[C]//Proc of the WebKDD 2000 Workshop at the ACM-SIGKDD Conf on Knowledge Discovery in Databases(KDD 2000),2000:1-12.
[5]Samatthiyadikun P，Takasu A，Maneeroj S.Multicriteria collaborative filtering by Bayesian model-based user profiling[J].Information Reuse and Integration(IRI),2012,59(5):124-131.
[6]高风荣,杜小勇,王珊.一种基于稀疏矩阵划分的个性化推荐算法[J].微电子学与计算机,2004,21(2):58-62.
[7]Pereira A L V，Hruschka E R.Simultaneous co-clustering and learning to address the cold start problem in recommender systems[J].Knowledge-Based Systems,2015,82:11-19.
[8]He J,Chu W,A Social Network-based Recommender System(SNSR)[M].[S.l.]:Springer US,2010:47-74.
[9]Shambour Q,Lu J.An effective recommender system by unifying user and item trust information for B2B applications[J].Journal of Computer and System Sciences,2015,81(7):1110-1126.
[10]Balabanovic M,Shoham Y,Fab:content-based collaborative recommendation[J].Communications of the ACM,1997,40(3):66-72.
[11]田保军，胡培培，杜晓娟，等.Hadoop下基于聚类协同过滤推荐算法优化的研究[J].计算机工程与科学,2016,38(8):1615-1624.
[12]Su H，Zhu Y，Wang C，et al.Parallel collaborative filtering recommendation model based on expand-vector[C]//Proceedings of the IEEE Second International Conference on Cognitive Systems and Information Processing,Beijing,China,2014:102-113.
八．代码

import numpy as np
import pandas as pd
from pandas import Series,DataFrame

##以下为找出两个相似度最大的用户
rnames = ['user_id','movie_id','rating','timestamp']
ratings = pd.read_csv('./u1.test',sep='\t',header=None,names=rnames)
data = ratings.pivot(index='user_id',columns='movie_id',values='rating')
print(data[:10])
foo = DataFrame(np.empty((len(data.index),len(data.index)),dtype=int),
                index=data.index, columns=data.index)
#print(len(data.index))
'''
for i in foo.index:
    for j in foo.columns:
        foo.loc[i, j] = data.loc[i][data.loc[j].notnull()].dropna().count()
#print(foo.loc[i,j])
for i in foo.index:
    foo.loc[i, i] = 0
ser = Series(np.zeros(len(foo.index)))
for i in foo.index:
    ser[i] = foo[i].max()
'''
#print(ser.idxmax())  # 返回ser的最大值所在的行号
#print(ser[416])     # 取得最大值
#print(foo[foo == 58][416].dropna())    # 取得另一个 user_id
#print(data.loc[13].corr(data.loc[276]))    #计算两个用户的相关度


##把两个用户评分情况放到test表里,并随机抽取两用户的样本值来估计min_periods参数值
test = data.reindex([13, 276], columns=data.loc[13][data.loc[276].notnull()].dropna().index)
#print(test)
#test.loc[276].value_counts(sort=False).plot(kind='bar')
periods_test = DataFrame(np.zeros((20,5)),columns=[5,10,15,20,30])
for i in periods_test.index:
    for j in periods_test.columns:
        sample = test.reindex(columns=np.random.permutation(test.columns)[:j])
        periods_test.loc[i,j] = sample.iloc[0].corr(sample.iloc[1])
#print(periods_test[:10])
#print(periods_test.describe())



##算法检验，判断min_periods参数值取得是否合适
#在评价数大于5的用户中随机抽取300位用户，每人随机提取一个评价另存到一个数组里，并在数据表中删除这个评价.
# 然后基于阉割过的数据表计算被提取出的 300 个评分的期望值，最后与真实评价数组进行相关性比较，看结果如何。
check_size = 300
check = {}
check_data = data.copy()  # 复制一份 data 用于检验，以免篡改原数据
check_data = check_data.loc[check_data.count(axis=1) > 10]  # 滤除评价数小于5的用户,axis=1表示沿每一行索引下去
#print(len(check_data))   #check_data=428
for user in np.random.permutation(check_data.index):
    movie = np.random.permutation(check_data.loc[user].dropna().index)[0]
    check[(user, movie)] = check_data.loc[user, movie]
    check_data.loc[user, movie] = np.nan
    check_size -= 1
    if not check_size:                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       
        break

corr = check_data.T.corr(min_periods=10)
corr_clean = corr.dropna(how='all')
corr_clean = corr_clean.dropna(axis=1, how='all')  # 删除全空的行和列
check_ser = Series(check)  # 这里是被提取出来的 300 个真实评分
#print(check_ser)
result = Series(np.nan, index=check_ser.index)
for user, movie in result.index:  # 这个循环看着很乱，实际内容就是加权平均而已
    prediction = []
    if user in corr_clean.index:
        corr_set = corr_clean[user][corr_clean[user] > 0.1].dropna()  # 仅限大于 0.1 的用户
    else:
        continue
    for other in corr_set.index:
        if not np.isnan(data.loc[other, movie]) and other != user:  # 注意bool(np.nan)==True
            prediction.append((data.loc[other, movie], corr_set[other]))
        if prediction:
         result[(user, movie)] = sum([value * weight for value, weight in prediction]) / sum(
            [pair[1] for pair in prediction])

result.dropna(inplace=True)
#print(len(result))  # 随机抽取的 300 个用户中也有被 min_periods=10 刷掉的，刷掉132个
#print(result.corr(check_ser.reindex(result.index)))
#print((result-check_ser.reindex(result.index)).abs().describe())

def user_based_cf():
    rnames = ['user_id', 'movie_id', 'rating', 'timestamp']
    ratings = pd.read_csv('./u1.test', sep='\t', header=None, names=rnames)
    data = ratings.pivot(index='user_id', columns='movie_id', values='rating')
    corr = data.T.corr(min_periods=5)
        #print(corr)

    corr_clean = corr.dropna(how='all')
        #print(corr_clean)

    corr_clean = corr_clean.dropna(axis=1, how='all')
    lucky = np.random.permutation(corr_clean.index)[0]

    gift = data.loc[lucky]
    gift = gift[gift.isnull()]
    corr_lucky = corr_clean[lucky].drop(lucky)  # lucky 与其他用户的相关系数 Series，不包含 lucky 自身
    corr_lucky = corr_lucky[corr_lucky > 0.1].dropna()  # 筛选相关系数大于 0.1 的用户
    for movie in gift.index:  # 遍历所有lucky没看过的电影
        prediction = []
        for other in corr_lucky.index:  # 遍历所有与lucky 相关系数大于 0.1 的用户
            if not np.isnan(data.loc[other, movie]):

                prediction.append((data.loc[other, movie], corr_clean[lucky][other]))
        if prediction:
            gift[movie] = sum([value * weight for value, weight in prediction]) / sum([pair[1] for pair in prediction])
    return gift.dropna().sort_values(ascending=False)

def main():
    list = user_based_cf()
    print(list)


if __name__ == "__main__":
    main()