(C/C++)STL函数（3）二分算法题以及二分模板 和（蓝桥杯）递推与递归题目及解法(ACwing)

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 前言
• 一、STL函数:双端队列、set和multiset两个容器.
• 二、二分算法（数的精度）
• 三、（蓝桥杯）递推与递归题目及解法(ACwing)
• 总结

---

前言

本篇文章为大家简要介绍STL库函数和蓝桥杯递推和递归题目及其相应解法

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、STL函数

1、#include
        双端队列deque是一个支持在两端高效插入或删除元素的连续线性存储空间。它就像是vector和queue的结合。与vector相比，deque在头部增删元素仅需要 O(1)O(1) 的时间；与queue相比，deque像数组一样支持随机访问。

[]              // 随机访问
begin/end       // 返回deque的头/尾迭代器
front/back      // 队头/队尾元素
push_back       // 从队尾入队
push_front      // 从队头入队
pop_back        // 从队尾出队
pop_front       // 从队头出队
clear           // 清空队列

2、 #include
        头文件set主要包括set和multiset两个容器，分别是“有序集合”和“有序多重集合”，即前者的元素不能重复，而后者可以包含若干个相等的元素。set和multiset的内部实现是一棵红黑树，它们支持的函数基本相同。

2.2 size/empty/clear
与vector类似

2.3 迭代器
set和multiset的迭代器称为“双向访问迭代器”，不支持“随机访问”，支持星号*解除引用，仅支持++和--两个与算术相关的操作。

设it是一个迭代器，例如set::iterator it;

若把it ++，则it会指向“下一个”元素。这里的“下一个”元素是指在元素从小到大排序的结果中，排在it下一名的元素。同理，若把it --，则it将会指向排在“上一个”的元素。

2.4 begin/end
返回集合的首、尾迭代器，时间复杂度均为 O(1)O(1)。

s.begin()是指向集合中最小元素的迭代器。

s.end()是指向集合中最大元素的下一个位置的迭代器。换言之，就像vector一样，是一个“前闭后开”的形式。因此-- s.end()是指向集合中最大元素的迭代器。

2.5 insert
s.insert(x)把一个元素x插入到集合s中，时间复杂度为 O(logn)O(logn)。

在set中，若元素已存在，则不会重复插入该元素，对集合的状态无影响。

2.6 find
s.find(x)在集合s中查找等于x的元素，并返回指向该元素的迭代器。若不存在，则返回s.end()。时间复杂度为 O(logn)O(logn)。

2.7 lower_bound/upper_bound
这两个函数的用法与find类似，但查找的条件略有不同，时间复杂度为 O(logn)O(logn)。

s.lower_bound(x)查找大于等于x的元素中最小的一个，并返回指向该元素的迭代器。

s.upper_bound(x)查找大于x的元素中最小的一个，并返回指向该元素的迭代器。

2.8 erase
设it是一个迭代器，s.erase(it)从s中删除迭代器it指向的元素，时间复杂度为 O(logn)O(logn)。

设x是一个元素，s.erase(x)从s中删除所有等于x的元素，时间复杂度为 O(k+logn)O(k+logn)，其中 kk 是被删除的元素个数。

2.9 count
s.count(x)返回集合s中等于x的元素个数，时间复杂度为 O(k+logn)O(k+logn)，其中 kk 为元素x的个数。（ACWing)

#include 
#include 
using namespace std;

int main ()
{
    set  a;// 元素不能重复
    multiset  b; // 元素可以重复
    
    struct Rec
    {
        int x, y;
        bool operator <(const Rec& t) const//重载小于号
        {
            return x < t.x;
        }
        set  c;//set定义一个结构体
    }
    set ::iterator it = a.begin();//定义一个迭代器
    it ++;//有序数对中加加
    it--;
    a.end();//表示最后一个元素的后一个数
    
    a.insert(x);
    if(a.find(x) == a.end()); //判断x在a中是否存在。
    a.low_bound(x);//找到大于等于x的最小的元素的迭代器
    a.upper_bound(x);//查找大于x的元素中最小的一个
    a.erase(x);//从a中删除迭代器x指代的元素
    a.count(x);
    return 0;
}

二、二分算法（数的精度）

 数的范围​​​​​​​

给定一个按照升序排列的长度为 nn 的整数数组，以及 qq 个查询。

对于每个查询，返回一个元素 kk 的起始位置和终止位置（位置从 00 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 nn 和 qq，表示数组长度和询问个数。

第二行包含 nn 个整数（均在 1∼100001∼10000 范围内），表示完整数组。

接下来 qq 行，每行包含一个整数 kk，表示一个询问元素。

输出格式

共 qq 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤1000001≤n≤100000
1≤q≤100001≤q≤10000
1≤k≤100001≤k≤10000

输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

3 4
5 5
-1 -1

#include
#include
#include
#include
using namespace std;

const int N = 100010;
int n, m;//n是数组长度，m表示查询次数
int q[N];
int main ()
{
    cin >> n >> m;
    for(int i = 0; i < n; i++) cin >> q[i];
    
    for(int i = 0; i < m; i++)
    {
        int x;
        cin >> x;
        int l = 0, r = n - 1;//定义左右两端点
        while(l < r)//递归求左端点
        {
            int mid = l + r >> 1;//l + r 除以2
            if(q[mid] >= x) r = mid;//说明q[mid]在答案右边此时mid的值赋给右边界
            else l = mid + 1;//否则q[mid]在答案左边此时mid+1的值赋给左边界
        }
        if(q[r] == x)
        {
            cout << r << ' ';//如果q[r] == x说明找到了起始的左边界并且输出
            r = n - 1;
            while(l < r)//递归求右端点
            {
                int mid = r + l + 1 >> 1;//mid 要加一是为了防止死循环
                if(q[mid] <= x) l = mid;//说明q[mid]在答案左边此时mid的值赋给左边界
                else r = mid - 1;//否则q[mid]在答案右边此时mid-1的值赋给右边界
            }
            cout << l << endl;
        }
        else cout << "-1 -1" << endl;
    }
    return 0;
}

 三、（蓝桥杯）递推与递归题目及解法(ACwing)

1、递归实现指数型枚举​​​​​​​​​​​​​​

从 1∼n1∼n 这 nn 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 nn。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 11 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1≤n≤151≤n≤15

输入样例：

3

输出样例：

3
2
2 3
1
1 3
1 2
1 2 3

#include 
#include 
#include 
#include 
using namespace std;

const int N = 20;//数组开大些
int st[N];//表示每个位置的当前状态，0表示还没考虑，1表示选他，2表示不选
int n;

void dfs(int u)
{
    if (u > n) //从1 开始，当 u > n 时表示已经到边界了
    {
        for(int i = 1; i <= n; i++)
        if(st[i] == 1)
            printf("%d ", i);
            printf("\n");
        return;
    }
    st[u] = 2;
    dfs(u + 1); //第一个分支，不选
    st[u] = 0;//恢复现场

    st[u] = 1;
    dfs(u + 1);//第二个分支,选
    st[u] = 0;

}
int main ()
{
    cin >> n;

    dfs(1);//从0位到n-1 位
    return 0;
}

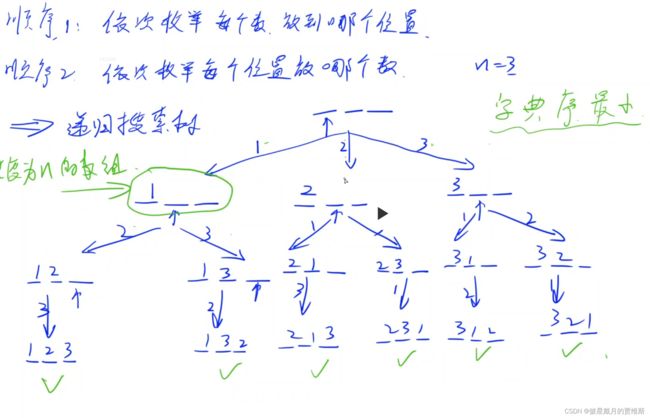
 2、递归实现排列型枚举​​​​​​​​​​​​​​

把 1∼n1∼n 这 nn 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 nn。

输出格式

按照从小到大的顺序输出所有方案，每行 11 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围

1≤n≤91≤n≤9

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

闫学灿老师画的递归搜索树

 

---

#include
#include
#include
#include
using namespace std;

const int N = 10; 
int n;
int st[N];//0表示还没放数，1到n表示放的数
bool used[N];

void dfs(int u)
{
    if(u > n)
    {
        for(int i = 1; i <= n; i++) printf("%d ", st[i]);
        puts("");
        return;
    }
    //依次枚举每个分支，即当前位置可以填哪些数
    for(int i = 1; i <= n; i++)
    if(!used[i])
    {
        st[u] = i;
        used[i] = true;
        dfs(u + 1);
        //恢复现场
        st[u] = 0;
        used[i] = false;
    }
}
int main ()
{
    cin >> n;
    dfs(1);
    return 0;

}

 

 

总结

提示：这里对文章进行总结：
本文主要是作者从ACWing学习的内容与大家分享，简要介绍了STL函数，二分算法题以及二分模板 和（蓝桥杯）递推与递归题目及解法，希望对读者有所启发。