【PyG】理解MessagePassing过程,GCN demo详解
文章目录
- PyG的信息传递机制
- MessagePassing Class
- GCN demo
-
- 1. 导入头文件
- 2. 构造函数
- 3. 前向传播forward
- 4. message
- 5. aggregate
- 6. update
- 完整GCN demo代码
参考:
PyG利用MessagePassing实现GCN(了解pyG的底层逻辑)
PyG官方demo GCN
PyG的信息传递机制
PyG提供了信息传递(邻居聚合) 操作的框架模型。
x i k = γ k ( x i k − 1 , □ j ∈ N ( i ) ϕ ( x i k − 1 , x j k − 1 , e j , i ) ) x_i^k = \gamma^k(x_i^{k-1}, \square_{j \in \mathcal{N}(i)} \phi(x_i^{k-1},x_j^{k-1},e_{j,i})) xik=γk(xik−1,□j∈N(i)ϕ(xik−1,xjk−1,ej,i))
其中,
□ \square □ 表示 可微、排列不变 的函数,比如说sum、mean、max
γ \gamma γ 和 ϕ \phi ϕ 表示 可微 的函数,比如说 MLP
在propagate中,依次会调用message,aggregate,update函数。
其中,
message为公式中 ϕ \phi ϕ 部分
aggregate为公式中 □ \square □ 部分
update为公式中 γ \gamma γ 部分
MessagePassing Class
PyG使用MessagePassing类作为实现 信息传递 机制的基类。我们只需要继承其即可。
GCN demo
GCN信息传递公式如下:
x i k = ∑ j ∈ i ∪ { i } 1 d e g ( i ) ⋅ d e g ( j ) ⋅ ( Θ T ⋅ x j k − 1 ) x_i^k = \sum_{j \in \mathcal{i} \cup \{i\}} {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } \cdot (\Theta^T \cdot x_j^{k-1}) xik=j∈i∪{i}∑deg(i)⋅deg(j)1⋅(ΘT⋅xjk−1)
注:GCN是运行在 无向图 上的。
1. 导入头文件
from typing import Optional
from torch_scatter import scatter
import torch
import numpy as np
import random
import os
from torch import Tensor
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
2. 构造函数
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super().__init__(aggr='add') # "Add" aggregation (Step 5).
self.lin = torch.nn.Linear(in_channels, out_channels)
定义类GCNConv继承MessagePassing。
aggr定义了聚合函数的作用。这里add表示累加。
当然,我们也可以通过重写aggregate方法,来自定义 聚合函数。
定义了线性变换层lin,也就是公式中的 Θ \Theta Θ。不过,与公式不同的是,这里的lin是有偏置bias的。
3. 前向传播forward
def forward(self, x, edge_index):
# x.shape == [N, in_channels]
# edge_index.shape == [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
# Step 4-5: Start propagating messages.
return self.propagate(edge_index, x=x, norm=norm)
定义 神经网络的 前向传播 过程。
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
添加自环。
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
计算 Θ ⋅ x \Theta \cdot x Θ⋅x
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
计算 系数,也就是公式中的
1 d e g ( i ) ⋅ d e g ( j ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } deg(i)⋅deg(j)1
这里有点难理解。可以根据 张量的形状 进行理解。
row表示出边的顶点,col表示入边的顶点。
注:PyG是支持有向图的,所以
(0,1), (1,0)一起表示无向图中的一条边。
degree计算 入顶点的度数。但,由于GCN运行在无向图上,其实 入顶点个数 == 顶点个数。
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0 把度数为0的节点去掉,因为他们是无穷大。
最后结果得到的norm 表示的含义是,边上两个节点度数乘积。即,每条边表示 1 d e g ( i ) ⋅ d e g ( j ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } deg(i)⋅deg(j)1 一个权重系数。
4. message
def message(self, x_i, x_j, norm):
# x_j ::= x[edge_index[0]] shape = [E, in_channels]
# x_i ::= x[edge_index[1]] shape = [E, in_channels]
# norm.view(-1, 1).shape = [E, 1]
# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j
定义 信息传递函数。
有同学会问,
x_i, x_j哪里来的?
PyG为我们提供的。
其中,MessagePassing默认信息流向flow为source_to_target。若存在边(0,1),那么 信息流向 为0->1。
x_j就是source点,x_i就是target点。
norm.view(-1, 1) * x_j,将 边上的权重 乘上 source点的特征。即完成了 1 d e g ( i ) ⋅ d e g ( j ) ⋅ ( Θ T ⋅ x j k − 1 ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } \cdot (\Theta^T \cdot x_j^{k-1}) deg(i)⋅deg(j)1⋅(ΘT⋅xjk−1)。
5. aggregate
def aggregate(self, inputs: Tensor, index: Tensor,
ptr: Optional[Tensor] = None,
dim_size: Optional[int] = None) -> Tensor:
# 第一个参数不能变化
# index ::= edge_index[1]
# dim_size ::= [number of node]
# Step 5: Aggregate the messages.
# out.shape = [number of node, out_channels]
out = scatter(inputs, index, dim=self.node_dim, dim_size=dim_size)
return out
定义 聚合函数。
其实,到这步 我们可以不用写了,因为之前的aggr="add"就已经足够了。
index参数 由 PyG提供,为 入顶点的编号。
torch_scatter.scatter函数 简单的说,就是把 编号相同 的属性[累加、求最大、求最小]聚集在一起。
下面这张图为,scatter求最大。
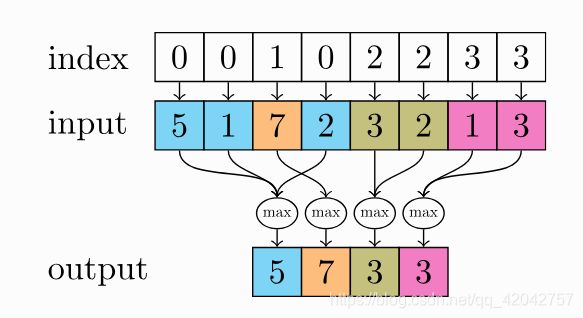
详见:
pytorch:torch_scatter.scatter_max
torch.scatter与torch_scatter库使用整理
6. update
def update(self, inputs: Tensor, x_i, x_j) -> Tensor:
# 第一个参数不能变化
# inputs ::= aggregate.out
# Step 6: Return new node embeddings.
return inputs
使用得到的 信息,更新当前节点的信息。
inputs为 更新得到的信息,其实就是 aggregate的输出。
update 对应了 公式中的 γ \gamma γ 。
注意:第一个参数 为
aggregate的输出。可改名字,但不能换位置。
完整GCN demo代码
from typing import Optional
from torch_scatter import scatter
import torch
import numpy as np
import random
import os
from torch import Tensor
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super().__init__(aggr='add') # "Add" aggregation (Step 5).
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# x has shape [N, in_channels]
# edge_index has shape [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
# Step 4-6: Start propagating messages.
return self.propagate(edge_index, x=x, norm=norm)
def message(self, x_i, x_j, norm):
# x_j ::= x[edge_index[0]] shape = [E, in_channels]
# x_i ::= x[edge_index[1]] shape = [E, in_channels]
print("x_j", x_j.shape, x_j)
print("x_i: ", x_i.shape, x_i)
# norm.view(-1, 1).shape = [E, 1]
# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j
def aggregate(self, inputs: Tensor, index: Tensor,
ptr: Optional[Tensor] = None,
dim_size: Optional[int] = None) -> Tensor:
# 第一个参数不能变化
# index ::= edge_index[1]
# dim_size ::= [number of node]
print("agg_index: ",index)
print("agg_dim_size: ",dim_size)
# Step 5: Aggregate the messages.
# out.shape = [number of node, out_channels]
out = scatter(inputs, index, dim=self.node_dim, dim_size=dim_size)
print("agg_out:",out.shape,out)
return out
def update(self, inputs: Tensor, x_i, x_j) -> Tensor:
# 第一个参数不能变化
# inputs ::= aggregate.out
# Step 6: Return new node embeddings.
print("update_x_i: ",x_i.shape,x_i)
print("update_x_j: ",x_j.shape,x_j)
print("update_inputs: ",inputs.shape, inputs)
return inputs
def set_seed(seed=1029):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed) # 为了禁止hash随机化,使得实验可复现
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # if you are using multi-GPU.
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
if __name__ == '__main__':
set_seed(0)
# x.shape = [5, 3]
x = torch.tensor([[1,2], [3,4], [3,5], [4,5], [2,6]], dtype=torch.float)
# edge_index.shape = [2, 6]
edge_index = torch.tensor([[0,1,2,3,1,4], [1,0,3,2,4,1]])
print("num_node: ",x.shape[0])
print("num_edge: ",edge_index.shape[1])
in_channels = x.shape[1]
out_channels = 3
gcn = GCNConv(in_channels, out_channels)
out = gcn(x, edge_index)
print(out)
PyTorch固定随机数种子
固定住 随机数种子 后,多次运行,比较好 比较 与 理解。