【力扣刷题笔记（二）】特别技巧，模块突破，45道经典题目分类总结，在不断巩固中精进

希望大家都能：简单题 重拳出击，中等题信手拈来，困难题想想能做

必会的基础算法：贪心，双指针，二分，搜索，动态规划。还没掌握的可以从这里开始哦：
【力扣刷题笔记】由简到难，模块突破， 你与AC只差一句提示。https://blog.csdn.net/weixin_44179010/article/details/123847312

下面是数学技巧、位运算、基础数据结构 模块， 45道经典题目助你透彻理解、运用自如。
有用可以收藏，记得点赞！

一、巧妙的数学

复杂的数学问题没有通用解法，但是经典的数学套路一定要掌握哦~ 比如： 最大公约数、最小公倍数、质数、数字处理、随机与采样。

1.1 公倍数与公因数

利用辗转相除法，我们可以很方便的求得两个数得最大公因数，再有最大公因数得出最小公倍数。

如果对辗转相除法不是很理解，可以这样想：
a 和 b 代表两个不同长度的线段。 假设 a 比较长。 如果长线 a 是短线 b 的整数倍，那么最大公约数就是短线 b 的长度
如果不是整数倍， 我们先把长线 a 中 短线 b 的整数倍取出来， 剩下的部分，和短线 b 的最大公约数和之前是相同的。
因为最大公约数相当于最大量度， 能整倍取出的部分不会影响这个量度， 多出来的那一部分才会决定它们的量度

    public int gcd(int a, int b) {
        return b != 0 ? gcd(b, a % b) : a;
    }

知道了最大公约数，最小公倍数就简单了 直接 a * b 再除以最大公约数即可

    public int lcm(int a, int b) {
        return a * b / gcd(a, b);
    }

1.2 质数

质数又称素数，指：一个大于 1 的自然数，除了 1 和它本身，没有不在有其他因数。比如 2、 3、 5、 7、 11、 13、17、 19
值得注意的是： 任何大于 1 的整数，都可以分解成质数的乘积，且如果不考虑次序的话这个分解是唯一的

204.计数质数

题目： 给你一个整数n， 求小于 n 的所有的质数个数。

i 从 2 遍历到 n， 遍历过程中把 i 之后的且是 i 的倍数的数进行标记，遍历完之后，没被标记的就是质数

        if(n <= 2) return 0;
        int count = n - 2;  //去掉 1 和 0
        boolean[] notPrimes = new boolean[n];
        for(int i = 2; i < n; i++) {
            if(!notPrimes[i]) {
                for(int j = 2 * i; j < n; j += i) {
                    if(!notPrimes[j]) {
                        notPrimes[j] = true;
                        count--;
                    }
                }
            }
        }
        return count;

1.3 数字处理

504.七进制数

给你一个十进制数，转化成7进制数的字符串
输入：100
输出：“202” —解释：100 = 2 * 49 + 0 * 7 + 2 * 1

Java API ：

return Integer.toString(num, 7);

进制转换一般利用除法和取模进行计算， 类似十进制取出每位的数。取出七进制每位的数再拼接起来就行了。

while (num != 0) {
      sb.append(num % 7); //最低位到最高位
      num /= 7;
 }

172.阶乘后的零

给你一个整数，求这个数的阶乘结尾有几个0；

尾部的 0 是 由 2 x 5 而来的， 把阶乘中每个数都拆成质数相乘，统计有多少个 2 和 5. 由于 2 的个数一定是远多于 5 的个数的，所有只需统计 5 的个数。 6 之前有 1 个 5 ， 25 之前有 6个5【5、10、15、20、5、5】

    public int trailingZeroes(int n) {
        return n == 0 ? 0 : n / 5 + trailingZeroes(n / 5);
    }

326.3的幂

判断一个数，是否是3的整数次方。

两种办法：

1. 利用对数， ${\log }_3^n=m$， 如果 n 是 3 的整数次方，那么m一定是整数。由换底公式：${\log }_3^n=\frac{{\log }_{10}^n}{{\log }_{10}^3}$
2. 由于3的幂次的质因子只有3，利用3的次方的最大数， 在 int 范围 3的最大次方数是 $3^{19}$, 如果 n 是 3 的整数次方，那么一定能被这个数整除，反正亦然，注意 n 小于0 的情况直接返回。

        double tem = Math.log10(n) / Math.log10(3);
        return tem == (int)tem;

1.4 随机与采样

384.打乱数组

给你一个数组， 实现两个指令函数，第一个随机打乱这个数组，第二个恢复这个数组。

把原始数组保存下来，恢复的时候直接恢复。打乱数组可以用洗牌算法。即遍历数组，把位置 i 的数字和其他随机位置的数字交换。
打乱数组代码：

    public int[] shuffle() {
        int[] tem = nums.clone();
        for(int i = 0; i < tem.length; i++) {
            swap(i, r.nextInt(tem.length), tem); //位置 i 数字 和 随机位置交换
        }
        return tem;
    }

练习

168.Excel表列名称

给你一个整数 columnNumber ，返回它在 Excel 表中相对应的列名称。
A – 1
Z – 26
AA–27
AB–28

26进制变种， 注意这里是1-26, 不是0-25， 所有取余和相除的时候得注意

        char[] arr = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M',
        'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z'};
        StringBuilder sb = new StringBuilder();
        while(columnNumber != 0) {
            int num = ((columnNumber % 26 - 1) + 26) % 26; // 余1 对应 0 ， 余0 对应 25
            sb.append(arr[num]);
            columnNumber = (columnNumber - 1) / 26; // 26 对应 25。再除以 26
        }
        return sb.reverse().toString();

67.二进制求和

给你两个二进制数字得字符串， 计算相加后的二级制字符串

思路： 模拟。 模拟进位即。

238.除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

思路： 类似前缀和思想，answer[i] = 左边的积 * 右边的积

        int[] ret = new int[nums.length];
        //左边乘积 
        int sum = 1;
        for(int i = 0 ; i < nums.length; i++) {
            ret[i] = sum;
            sum *= nums[i];
        }
        //* 右边乘积
        sum = 1;
        for(int i = nums.length - 1 ; i >= 0; i--) {
            ret[i] *= sum; //左边乘积 * 右边乘积 
            sum *= nums[i];
        }
        return ret;

462.最少移动次数使数组元素相等II

给你一个整数数组， 每次可以使一个数 +1 或 -1, 求最少多少次能把所有数字变成相同的数字。

思路： 全变成中位数就是最优解。

169.多数元素

给你一个数组，返回多数元素，多数元素指出现次数 大于 ⌊ n/2 ⌋ 的元素

思路： 摩尔投票。
可以这样理解。每个不同的元素都是一个阵营，现在所有人大混战，所有人战斗力都是一样的也就是1v1 一定同归于尽。
如果有人数超过一半的阵营，那这个阵营一定是最后胜出者。

470.用Rand7()实现Rand10()

系统给你一个能实现生成1-7随机数的函数， 你在这个函数基础上写一个能生成1-10随机数的函数。不能借助其他内置函数。

生成1-10的随机数，即每个数的概率的 $\frac{1}{10}$ 。 $\frac{1}{2}\ast \frac{1}{5}=\frac{1}{10}$ ，所以只需得到一个生成概率为 $\frac{1}{2}$ 的数 和一个生成概率为 $\frac{1}{5}$ 的数

        int a = rand7(), b = rand7();
        while(a > 5) a = rand7(); // 1 / 5
        while(b == 7) b = rand7(); // b 为偶数的概率是 1/2
        return ((b & 1) == 0 ? 0 : 5) + a;

202.快乐数

快乐数，就是每位变成它的平方再相加，最后变成1。是快乐数就返回true
例如：n = 19
$1^2+9^2=82$
$8^2+2^2=68$
$6^2+8^2=100$
$1^2+0^2+0^2=1$
返回true

如果一个数是快乐数，那么它最后一定是变成 1 。
如果不是快乐数，分为两种情况：①陷入一个循环 ②无限递增不循环
分析无限递增的情况：$9^2=81$ 、$9^2+9^2=162$ 、$9^2+9^2+9^2=243$ 、$9^2+9^2+9^2+9^2=324$ 11个9 = 81*11=891
3位数收敛在243 以内， 4位数到11位数收敛在891（三位数），下一步一定也收敛在243以内。所以不存在无限递增的情况

最后只有两种情况 要么变成1，要么陷入一个不是1的循环中。
方法1： 做个标记，陷入循环返回false，得到1返回true
方法2： 快慢指针，由于它们一定陷入循环，要么是全为1的循环，要么是别的循环，类似快慢指针判断环形链表。
如果头碰到1了返回true， 如果头尾相遇了还没碰到1返回false
你快乐了吗

二、神奇的位运算

2.1 位运算常用技巧

最基础的位运算： 复习一遍吧 ：
<< 左移， >>右移， >>> 忽略符号位右移

除此之外，还有以下常用技巧 ，记忆一下吧！⭐️
-n = ~n + 1
n & (n - 1) 可以去除 n 的最低位的 1 比如 1010 --> 1000
n & (-n) 可以只保留 n 的最低位的 1 比如： 1010–> 0010
两个数异或，相当于无进位的加法。两个数相与， 可以得到进位位。

2.2 位运算基础

461.汉明距离

汉明距离是两个二进制数，二进制位不同的数目。 给你两个数返回汉明距离

二进制位不同的数目，也就是两个数异或一下，不同的地方变成了1，看异或的结果有几个1。

        int tem = x ^ y;
        int ret = 0;
        while(tem != 0) {
            ret++;
            tem &= tem - 1;//每次去除最后一位1
        }
        return ret;

190.颠倒二进制位

给你一个32位的无符号数， 返回左右翻转后得到的二进制数。
比如：输入11111111111111111111111111111101 返回 10111111111111111111111111111111对于的数

思路： 位运算，左移、右移来实现，第 1 位移到32位处， 第 2 位移到31位处… 第32位移到第1位处，32位全移动一遍就欧克了。

        int ret = 0;
        for(int i = 0; i < 32; i++) {
            ret |= (n & 1) << (31-i);
            n >>>= 1;
        }
        return ret;

136.只出现一次的数字

一个数组，里面有一个数字只出现了一次，其他都出现了两次

应为 x ^ x = 0, 且异或满足结合律，直接全部异或，把出现两次的清除。

        int ret = 0;
        for(int num : nums) {
            ret ^= num;
        }
        return ret;

2.3 二进制特性

我们可以创建一个数，把二进制每位的0 、 1当作一种标记，比如第一位为1， 表示选中了第一个选项。

342.4的幂

给你一个整数，判断他是不是 4 的整数次方。

法一： 和 3 的幂的方法 1 一样 ，利用对数， ${\log }_4^n=m$， 如果 n 是 4 的整数次方，那么m一定是整数

法二： 2的次幂二进制只有 1 个 1。 4 的 次幂也是，并且多一个限制条件， 1只能在奇数位置 。 1、 100、 10000、等
5二进制是0101，奇数位全为1

if (n < 0 || (n & (n-1)) != 0) return false; //有多个1， 或 < 0
return (n & 0x55555555) != 0; //只有一个1 且 奇数位为1；

318.最大单词长度乘积

给你一个字符串数组，返回其中两个字符串长度乘积的最大值， 且这两个字符串不能有相同字母。

思路： 首先得判定两个字符串有没有共同字母， 首先想到的可能是用HashSet存字母，两两判断。或者用 bool 数组标记字母，两两判断。
每次两两判断都遍历两人标记数组或集合，很浪费。 用二进制位表示是否有对于字母，两两直接相与即可得到是否有相同字母。

    public int maxProduct(String[] words) {
        int n = words.length;
        int[] flag = new int[n];
        for(int i = 0; i < n; i++) flag[i] = getFlag(words[i]);
       
        int ret = 0;
        for(int i = 0; i < n; i++) 
            for(int j = i + 1; j < n; j++) 
                if((flag[i] & flag[j])== 0) ret = Math.max(words[i].length() * words[j].length(), ret);     
        return ret;
    }
    int getFlag(String s) {
        int ret = 0;
        for(char c : s.toCharArray()) ret |= 1 << (c - 26);
        return ret;
    }

338.比特位计数

给你一个整数n， 返回0 - n 每个数的二进制数有几个1；返回的是一个长度为 n + 1 的数组

法一：可能最容易想到的遍历每个数， 计算这个是的二进制数 1 的个数。
计算二进制数个数可以用API， Integer.bitCount()， 也能用循环+ n & (n - 1) 消除最后一位

法二： 动态规划， 可以发现后面的数的二进制数，其实是前面某个较小的某位 0 变成 1 形成的。
假设我们用消除最后一位1来找到前面比他小的数， 那0001， 0010，0100，1000都可以由 0000推出。

        int[] ret = new int[n + 1];
        for(int i = 1; i < n + 1; i++) {
            ret[i] = ret[(i & (i - 1))] + 1;
        }
        return ret;

练习题

268.丢失的数字

给你长度为 n 的数组， 数组的数字从 [0, n] 这 n + 1个数中选的，数组里的数不重复。 返回哪个数没被选中。

哪个没选中呢？最简单方法： 求个和， 0 到 n 总和 - 数组总和 剩下的数不就是没选中的嘛

求和得两次遍历， [0, n] 和数组里的值合并起来， 丢失的数字不就是只出现一次的数字嘛。用异或即可得到。

        int ret = 0, n = nums.length;
        for(int i = 0; i < n; i++) {
            ret ^= nums[i] ^ i;
        }
        return ret ^ n;

693.交替位二进制数

给定一个正整数，检查它的二进制表示是否总是 0、1 交替出现

交替出现，最简单方法，从最低位第一位开始，设置一个标志位，进行0 1判断即可

        int pre = (n & 1);
        n >>= 1;
        while(n != 0) {
            int cur = (n & 1);
            if((pre ^ cur) == 0) return false;
            n >>= 1;
            pre = cur;
        }
        return true;

方法二： 不用循环遍历，如果是0 1 交替出现的，则 n ^ (n << 1) ==> 得到最高位1之前全为1， 即 00001010 ==> 00001111
怎么判断最高位及之前低位全是1呢？ 给这个数 + 1， 就变成最高位后一位高位为1其他为0， 即00001111 ==> 00010000。 两者相与必为0。

        int m = n ^ (n >> 1);
        return (m & (m + 1)) == 0;

476.数字的补数

对整数的二进制表示取反,再表示为十进制数。 前导0不算。

给每个位置赋值就好啦✌️

        int ret = 0;
        int count = 0;
        while(num != 0) {
            ret |= ((num & 1) == 1 ? 0 : 1 ) << count;
            num >>= 1;
            count++;
        }
        return ret;

260.只出现一次的数字III

给你一个数组，恰好有两个数只出现一次，其他数都是出现两次。 进阶：线性复杂度，常数空间

方法一：用Map，直接做。

进阶：线性复杂度，常数空间
恰好两个数只出现一次， 把数组分成两组，每组一个单独的数字，一组异或起来就可以得到拿个单独的数字。

有什么办法能使这些数分为两组，且一样的数字一定被分在同一组，个数为1的数字被分到不同组？
奇偶肯定不行，个数为 1 的数可能是奇数也可能是偶数。这个区分的标准一定和这两个数的特征相关。
怎么一次遍历就能获得这两个数的特征呢？ 全部异或起来， 相同的数的特征被变成了0， 结果相当于这只有两个数异或。
这两个数异或结果为1的位，就可以把两个数区分开。
因为两个数为异或结果为 1 的位 ，对于原始数字来说一定一个为 1 一个 为 0

怎么得到这个为 1 的位呢？ 可以用位运算获取最后一个1的位置即 n & (-n)

        int sum = 0;
        for(int num : nums) sum ^= num;
        int flag = sum & (-sum); //最后一个1的位
        int[] ret = new int[2];
        for(int num : nums) {
            //flag 那个位为 0 
            if((num & flag) == 0) ret[0] ^= num;
            else ret[1] ^= num;
        }
        return ret;

三、基础数据结构

3.1 数组

448.找到所有数组中消失的数字

给你一个数组， 数组里的数字是[1, n]， 返回[1, n]中数组中没出现的数字

方法很多。有个不用开新空间，用原始数组做标记的方法： 出现过的数A，将原始数组nums[A] 置为负数。最后为正的数的位置是没出现的数字

        for(int i = 0; i < nums.length; i++) {
            int cur = Math.abs(nums[i]);
            if(nums[cur - 1] > 0) nums[cur - 1] = - nums[cur - 1];
        }
        List<Integer> ret = new ArrayList<>();
        for(int i = 0; i < nums.length; i++) {
        	if(nums[i] > 0) ret.add(i + 1);
        }
        return ret;

48.旋转图像

给你一个二维矩阵，原地旋转90度。

思路： 模拟即可，可以找找规律，例如先转置，再交换左右列

240.搜索二维矩阵II

给你一个二维矩阵，已知每行每列都是递增的，设计可以能快速搜索一个数组是否在矩阵中的算法

从右上角， 大就往下，小就往左。到左下角还没有那就是无了

769.最多能完成排序的块

给你一个数组，数组包含数组0-n 每个数只出现一次。求这个数组最多可以分割成多少个子数组，使得子数组排序后，再拼起来仍是有序的。
例如：4 3 2 1 0 只能分成一块，子块排序后整体才是有序的
例如：0 3 2 1 5 4 能分成三块 【0】【3 2 1】【5 4】 子块排序后整体有序

思路：什么情况能拆成子块？ 数字大于索引的时候我们必须把他和后面的放到一块，好让他排序达到数字对应索引。 5 1 2 3 4 0， 只能分一块。数字大于索引，必须有足够的位置让这个数字放到对应索引

        int ret = 0, max = 0;
        for(int i = 0; i < arr.length; i++) {
            if(arr[i] == i) ret++;
            else {
                max = arr[i];
                while(i < max) {
                    i++;
                    max = Math.max(arr[i], max);
                }
                ret++;
            }
        }
        return ret;

3.2 栈和队列

232.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）

思路： 栈是先入后出， 队列是先入先出。 栈实现队列，入的时候直接放入一个栈1，放到栈顶
出的时候如果栈2为空就把栈1全弹入栈2，这样栈2的顶即为栈1 的底，如果栈2不为空，那栈2的顶一直都是栈1的低

155.最小栈

设计一个支持以O(n) 返回栈内最小值的最小栈

思路： 再加一个栈2，栈2里放栈1中的最小值， 如果栈 1 弹出了最小值，栈2也弹出，如果栈1新放入更小的值，就给栈2也加入更小值。

20.有效的括号

给定一个只由左右原括号、花括号、和方括号组成的字符串。求这个字符串是否合法。合法就是左右一一对应。

思路：左括号放栈里右括号和栈顶比，匹配不上就返回，匹配上就弹出

3.3 单调栈

单调栈通过维持栈内值的单调递增（递减）性，在整体O(n) 的时间内处理需要大小比较的问题

单调栈保证栈内元素单调递增（递减），代码框架：

        Stack<Integer> stack = new Stack<>();
        int[] nums = new int[]{9, 6, 4, 3, 1, 2, 6, 3};
        for (int num : nums) {
        	//如果栈顶元素小于要放入的元素，就弹出。
            while (!stack.isEmpty() && stack.peek() < num) {
                stack.pop();
               //
            }
            stack.push(num);
        }
        //看情况处理栈内剩余元素

更多练习和技巧：单调栈的运用思路及相关题解 https://blog.csdn.net/weixin_44179010/article/details/122278178

739.每日温度

给定一个数组，表示每日温度，求几天后会有更高的温度，如果没有更高的温度返回0
输入: [73, 74, 75, 71, 69, 72, 76, 73]
输出: [1, 1, 4, 2, 1, 1, 0, 0]

单调栈最简单的应用： 找到下一个更大（更小）的数。
维持一个单调递减的栈，一旦遇到更大的数就取出之前之前所有比他小的数，计算天数差。
为方便计算，栈内存放数组下标（即日期）

        Stack<Integer> stack = new Stack<>();
        int n = temperatures.length;
        int[] ret = new int[n];
        for(int i = 0; i < n; i++) {
            while(!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                int index = stack.pop();
                ret[index] = i - index; // 遍历到更大的数，就把之前较小的数取出，进行计算即可
            }
            stack.push(i);
        }
        //如果栈内还有元素，说明这些都是后几天没有更高温度的，天数返回为0，可以省略这一步
        return ret;

3.4 优先队列

优先队列可以在O(1)时间获取最大（最小）值， 可以在O(log(n))时间取出最大值或插入任意值
优先队底层是堆来实现的。堆是一个完全二叉树，每个节点的值总是大于等于子节点的值

如果对优先队列不了解，可以看看我另一篇博文：
优先队列用法及相关题目解题思路 https://blog.csdn.net/weixin_44179010/article/details/122127012

23.合并K个升序链表

给你一个链表数组，每个链表都是增序的，把这些链表合并成一个增序链表

优先队列，直接把链表放队列里，按照头节点值的大小升序，每次取出头最小的链表，得到这个最小值后，再把链表的next放回队列

用优先队列这道困难题很容易就秒了

        if(lists == null || lists.length == 0) return null;
        //创建小顶堆
        PriorityQueue<ListNode> priorityQueue  = new PriorityQueue<>((node1, node2) -> node1.val - node2.val);
        //把链表全放入小顶堆
        for(ListNode tem : lists) {
            if(tem == null) continue;
            priorityQueue.add(tem);
        }
        ListNode dump = new ListNode();
        ListNode cur = dump;
        while(!priorityQueue.isEmpty()) {
            //取出头最小的链表
            ListNode tem = priorityQueue.poll();
            cur.next = new ListNode(tem.val);
            cur = cur.next;
            //把链表下一个放回堆
            tem = tem.next;
            if(tem != null) priorityQueue.add(tem);
        }
        return dump.next;

218.天际线问题

给定建筑物起始位置和高度，返回建筑物轮廓线的拐点（水平线的左端点）

题目分析：关键点即水平线的左端点，从左到右扫描所以的边，可以发现，所以的关键点都在两条扫面线围成的矩形的左上角， 还要忽略没有高度后面没有高度变化的矩形。

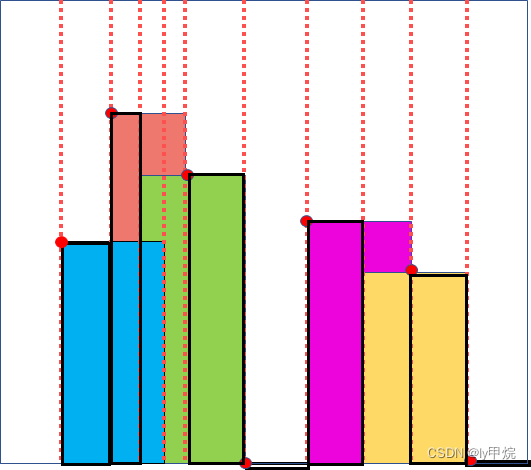
怎么确定扫描线维成的矩形的真实高度？

遍历到左端点的时候，记录一个高度，碰到更高的左端点记录更高的，获取最高高度
碰到右端点，就把右端点对应的高度去掉，再获取最高的高度
可以用优先队列实现这个功能

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        List<List<Integer>> ret = new ArrayList<>();
        int n = buildings.length;
        List<int[]> points = new ArrayList<>();
        for (int[] building : buildings) {
            int h = building[2];
            points.add(new int[]{building[0], h});  //左端点存正值，右端点存负值，便于区分左右端点
            points.add(new int[]{building[1], -h});
        }
        Collections.sort(points, (q, w) ->{
            if(q[0] != w[0]) return q[0] - w[0];
            //两个端点相等，得保证重合得时候下一个左端点在前面
            return w[1] - q[1];
        });

        int preH = 0;
        PriorityQueue<Integer> queue = new PriorityQueue<>((q, w) -> w - q);
        queue.add(preH);
        for (int[] point : points) {
            if(point[1] < 0) {
                // 如果是右端点，说明这条边结束了，将当前高度从队列中移除
                queue.remove(-point[1]);
            }else {
                // 如果是左端点，说明存在一条往右延伸的可记录的边，将高度存入优先队列
                queue.offer(point[1]);
            }
      
            // 取出最高高度，如果和前一个高度一样则不记录
            int cur = queue.peek();
            if (cur != preH) {
                List<Integer> list = new ArrayList<>();
                list.add(point[0]);
                list.add(cur);
                ret.add(list);
                preH = cur;
            }
        }
        return ret;
    }
}

主要参考：【宫水三叶】的题解

3.5 双端队列

双端队列：既能先入先出【获取底部数据】，也能先入后出。【获取顶部数据】。

239.滑动窗口最大值

给你一个整数数组nums 和一个整数 k ， 大小为 k 的滑动窗口从最左侧滑动到最右侧。返回滑动窗口中的最大值
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]

递增单调栈， 来一个小的放上面，来个大的，把小的踢出去。保证栈底到栈顶是递减的。
取底部就是最大的，最大的出去了就移除底部

    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] ret = new int[nums.length - k + 1];
        Deque<Integer> deque = new LinkedList<>();
        for(int i = 0; i < k - 1; i++) {
            // 递增单调栈， 来一个小的放上面，来个大的全出去，取底部就是最大的，最大的出去了就移除底部
            while(!deque.isEmpty() && nums[i] > deque.peekLast()) {
                deque.removeLast();
            }
            deque.offer(nums[i]);
        }
        //
        int left = 0;
        for(int i = k - 1; i < nums.length; i++) {
            while(!deque.isEmpty() && nums[i] > deque.peekLast()) { // 保证栈底到栈顶是递减的。
                deque.removeLast();
            }
            deque.offer(nums[i]);
            //System.out.println(deque);
            ret[i - k + 1] = deque.peekFirst();  // 取底部就是最大的
            if(deque.peekFirst() == nums[left++]) { //最大的出去了就移除底部
                deque.removeFirst();
            }
        }
        return ret;
    }

3.6 哈希表

1.两数之和

给定一个整数数组，已知有且只有两个数的和等于给定值，求这两个数的位置

哈希表key存数组的值， value存数组的索引，遍历hash表的key， 如果存在另一个key，使得两个key和为给定值，那就返回这两个key的value值，即这两个数的位置。

128.最长连续序列

字节一面原题。我干了一个排序，凉了。

给你个未排序的数组，找出数字连续的最长序列。 用时间复杂度为O(n)解决
输入：nums = [100,4,200,1,3,2]
输出：4 ， 解释： 最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

方法一：排序时间复杂度 O(nlogn)

方法二：用HashSet， 先放入，然后遍历数组找前后+1，2，3…和-1，-2，–3…的元素，找过的数字直接删除。最差O(2n)。

    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();

        for(int num : nums) {
            set.add(num);
        }
        int ret = 0;
        for(int num : nums) {
            if(!set.contains(num)) continue;

            int countInc = 0, countDec = 0;
            while(set.contains(num + countInc)) {
                set.remove(num + countInc);
                countInc++;
            }

            while(set.contains(num - countDec - 1)) {
                set.remove(num - countDec);
                countDec++;
            }
            if(countInc + countDec > ret) ret = countInc + countDec;
        }

        return ret;
    }

方法三： HashMap存每个值及其对应区间长度。每次找比他大1，2，3…的数。 从最小那个数开始往后找才是最长的，所有如果存在比这个数小1的数，就不从它开始找。最差O(2n)不用删除元素。
方法核心，从最小的数位置开始往后找。一段连续的数字，最小位置只有一个

    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums) set.add(num);
        int ret = 0;
        for(int num : set) {
            if(set.contains(num - 1)) continue;
            int count = 1;
            while(set.contains(num + count)) {
                count++;
            }
            if(count > ret) ret = count;
        }
        return ret;
    }

149.直线上最多的点

给你一个数组points, points[i] = [xi, yi] 表示X-Y平面上一个点，求最多多个点在一条直线上。

看数据长度，数组长度不大于300。可以疯狂暴力啦。

最简单的思路， 遍历所有点，计算这个点到其他点的斜率，斜率相同就是一条线的，用Map计数， 时间复杂度O(n²).
【一个点+斜率就可以唯一确定一条直线】
虽然是暴力遍历，还是要注意一些细节。 斜率应该用分数来存储，因为浮点数不准。
怎么化简为最简分数呢？ 两数都除以最大公约数。 当然这是分子分母都不为0， 如果分子为0，直接等于0，分母为0等于一个特殊值即可。

    public int maxPoints(int[][] points) {
        int ret = 1;
        int n = points.length;
        if(n <= 2) return n;
        for(int i = 0; i < n; i++) {
            if (ret >= n - i || ret > n / 2) break; //如果一条直线上的点的数量已经超过半数，那这条直线一定是点最多的直线
            Map<Integer, Integer> map  = new HashMap<>();
            for(int j = i + 1; j < n; j++) {
                int dx = points[i][0] - points[j][0];
                int dy = points[i][1] - points[j][1];
                if(dx == 0) dy = 1;
                else if(dy == 0) dx = 1;
                else {
                    if(dy < 0) {//负数提到前面
                        dy = -dy;
                        dx = -dx;
                    }
                    int gcdXY = gcd(Math.abs(dx), Math.abs(dy));
                    dx /= gcdXY;
                    dy /= gcdXY;
                }
                int k = dx * 20001 + dy ;
                map.put(k, map.getOrDefault(k, 1) + 1);
                ret = Math.max(ret, map.get(k));
            }
        }
        return ret;
    }

    public int gcd(int a, int b) {
        return b != 0 ? gcd(b, a % b) : a; 
    }

3.7 前缀和

一维、二维的前缀和，都是把每个位置之前的一维线段或二维矩形预先存储，方便加速计算。
通过前缀和，我们很容易获取到数组任意 [l ,r]的连续区间的和。后面的前缀和减前面的就是一段连续子数组[l ,r]区间和。
更多前缀和总结：看我的这篇文章 https://blog.csdn.net/weixin_44179010/article/details/121906773

303.区域和检索-数组不可变

一维前缀和简单应用

304.二维区域和检索-矩阵不可变

二维前缀和简单应用

560.和为K的子数组

给你一个整数数组 nums 和一个整数 k ，返回 该数组中和为 k 的子数组的个数 。

思路：拿到前缀和数组后，题目相当于返回前缀和数组，两两区间差为k的个数。

我们可以把前缀和存入Map中，后面得前缀和找前面是否存在相减为k的前缀和

        int n = nums.length;
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0,1);
        int sum = 0, ret = 0;
        for(int i = 0; i < n; i++) {
            sum += nums[i];
            if(map.containsKey(sum - k)) ret += map.get(sum - k);
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return ret;

简单练习题

566.重塑矩阵

实现MATLAB中的reshape函数， 把m * n 的矩阵重塑为 r * c 的， 如果不能重塑就返回原始矩阵

计算一下下标怎么对应的即可，很简单

225.队列实现栈

用两个队列实现一个栈

和之前用栈实现队列思路差不多。 核心是后来的放前头去.
每次放入一个空队列，然后之前的数全加入这个空队列，就把新来的放最下面了，出去的时候直接poll()。就把晚进来的先拿出去了

503.下一个更大的元素Ⅱ

返回下一个更大的元素，循环搜索， 没有返回 -1
输入: nums = [1,2,1]
输出: [2,-1,2]

和739每日温度类似。相当于数组首位拼接。用单调栈，遇到小的就先存着， 遇到更大的就把之前存的小的处理掉
（这个更大的数就是这些较小数的下一个更大的数）

        Deque<Integer> stack = new LinkedList<>();
        int n = nums.length;
        int[] ret = new int[n];
        Arrays.fill(ret, -1);
        for(int i = 0; i < n * 2; i++) {
            while(!stack.isEmpty() && nums[i % n] > nums[stack.peekLast()]) {
                ret[stack.removeLast()] = nums[i % n];
            }
            stack.offer(i % n);
        }
        return ret;

697.数组的度

给你一个数组nums， 包含数量最多的数的最短连续子数组。 如果数量最多的数有多个，就返回能包含其中一个的最短的子数组。
输入：nums = [1,2,2,3,1]
输出：2 解释：出现次数最多的数有1，2都出现了两次，最短的子数组是包含2的 [2,2]这个子数组，其长度为2，所以返回2

哈希表的题目, 哈希表把每个数字第一次出现位置，最后一次出现位置，总出现次数都存上

    public int findShortestSubArray(int[] nums) {
        //先找众数，再找众数最早和最晚出现的下标差
        //int[0] 第一次出现的位置  int[1]最后一次出现的位置， int[2] 出现次数
        Map<Integer, int[]> map = new HashMap<>();
        int max = 1;
        for(int i = 0; i < nums.length; i++) {
            if(map.containsKey(nums[i])) {
                map.get(nums[i])[1] = i;
                map.get(nums[i])[2]++;
                max = Math.max(max, map.get(nums[i])[2]);
            }else {
                map.put(nums[i], new int[]{i,i,1});
            }
        }
        int ret = nums.length;
        for(int[] values : map.values()) {
            if(values[2] == max) {
                ret = Math.min(ret, values[1] - values[0] + 1);
            }
        }
        return ret;
    }

594.最长和谐子序列

最大值和最小值差别刚好是1，叫和谐序列，给你一个数组，然后返回最长和谐子序列。

思路：统计所有数的个数，然后当前数数目 和 +1的数的数目总和。找最长的，没有+1的不统计。

class Solution {
    public int findLHS(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        int ret = 0;
        for(int num : nums) {
            if(map.containsKey(num + 1)) {
                ret = Math.max(map.get(num) + map.get(num + 1), ret);
            }
        }
        return ret;
    }
}

进阶练习题

287.寻找重复数

一个数组有 n + 1 个数， 这些数字都在[1，n]。至少存在一个重复多次的整数，返回这个重复的整数。要求不修改数组且O(1)额外空间
进阶：O(n) 时间复杂度

方法一：二进制
算[1-n]所有的二进制累加，每位有多少个1，算nums数组每位多少个1，相减。多出来的1一定是重复数多出来的。

        int[] dic = new int[32];
        for(int i = 0; i < nums.length; i++) {
            for(int j = 0; j < 32; j++) {
                dic[j] += (nums[i] & (1 << j));
                if(i > 0) {
                    dic[j] -= (i & (1 << j));
                }
            }
        }
        int ret = 0;
        for(int i = 0; i < 32; i++) {
            if(dic[i] > 0) ret |= (1 << i);
        }
        return ret;

方法二：快慢指针，Floyd判圈
Floyd判圈，又称龟兔赛跑算法，判断环形链表入口的时候我们用过： https://blog.csdn.net/weixin_44179010/article/details/122132496

数组长度是 n + 1, 里面所有的数都是 [1,n], 碰到一个数就去访问索引为这个数的数，由于所有的数都大于0，所有索引0处一定在环外。
如果长度是 n ，且没有重复的数字，那一定会遍历完所有情况才会形成一个大环，其中出现了重复数字里面就会进入这个小环。
用快慢指针+Floyd判圈，得到环的入口位置即为重复数字

Floyd判圈， 两人相遇了就一个人回到头部，然后都一步一步走，最终在入口处相遇

        int slow = 0, fast = 0;
        slow = nums[slow];
        fast = nums[fast];
        fast = nums[fast];
        while(nums[slow] != nums[fast]) {
            slow = nums[slow];
            fast = nums[fast];
            fast = nums[fast];
        }
        
        slow = 0;
        while(nums[slow] != nums[fast]) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return nums[fast];

313.超级丑数

超级丑数 是一个正整数，并满足其所有质因数都出现在质数数组 primes 中。
给你一个质数数组primes, 返回你 n 个超级丑数
输入：n = 12, primes = [2,7,13,19]
输出：32 解释：给定长度为 4 的质数数组 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。

之前的超级丑数 * primes 中每一个数即可。用优先队列保证顺序，发现重复的数就弹出

        PriorityQueue<Long> queue = new PriorityQueue<>();
        long ret = 1;
        for(int i = 1; i < n; i++) {
            for(int prime : primes) {
                queue.offer(prime * ret);
            }
            ret = queue.poll();
            while(!queue.isEmpty() && queue.peek() == ret) queue.poll(); //把重复的数弹出，保证每次取得都是从小到大第 i 个丑数
        }
        return (int)ret;

870.优势洗牌

给你两个长度相同的数组， 改变数组1的顺序，使得数组1[i] > 数组2[i]的数量最多。 题目类似于田忌赛马
输入：nums1 = [2,7,11,15], nums2 = [1,10,4,11]
输出：[2,11,7,15]

这题很明显是一个贪心问题， 类似最开始做的分发饼干。

类似田忌赛马。数组1最大的数对上数组二最大的数，如果更大，就放着。如果比不过就把最小的拿过来放着

这里我们要从大到小获取nums2的值已经对应索引， 所以用优先队列，存入值和索引。
对nums1排序。以便方便的拿到最大值和最小值

        int n = nums2.length;
        int[] ret = new int[n];

        PriorityQueue<int[]> queue = new PriorityQueue<>((q,w) -> w[0] - q[0]);
        for(int i = 0; i < n; i++) {
            queue.offer(new int[]{nums2[i], i});
        }
        Arrays.sort(nums1);
        int right = n - 1, left = 0;
        for(int i = 0; i < n; i++) {
            int[] tem = queue.poll();
            if(nums1[right] > tem[0]) {
                ret[tem[1]] = nums1[right--];
            }else {
                ret[tem[1]] = nums1[left++];
            }
        }
        return ret;

如果发现有错误的地方，欢迎大家提出批评指正。

致力于分享记录各种知识干货，关注我，让我们一起进步，互相学习，不断创作更优秀的文章。
希望大家能多多支持，你们的支持是我最大的动力！不要忘了三连哦 ⭐️
下篇预告：攻破复杂数据结构：字符串问题+链表+树+字典树+图+欧拉分路+并查集