3D点云 (Lidar)检测入门篇 - PointPillars PyTorch实现

3D点云 (Lidar)检测入门篇 - PointPillars PyTorch实现

完整代码:https://github.com/zhulf0804/PointPillars。

自动驾驶中基于Lidar的object检测，简单的说，就是从3D点云数据中定位到object的框和类别。具体地，输入是点云$\mathbf{X}\in {\mathbb{R}}^{N\times c}$ (一般$c=4$)，输出是$n$个检测框bboxes, 以第$i$个检测框bbox为例, 它包括位姿信息$(x_i,y_i,z_i,w_i,l_i,h_i,{\theta }_i)$和类别信息$({\text{label}}_i,{\text{score}}_i)$。

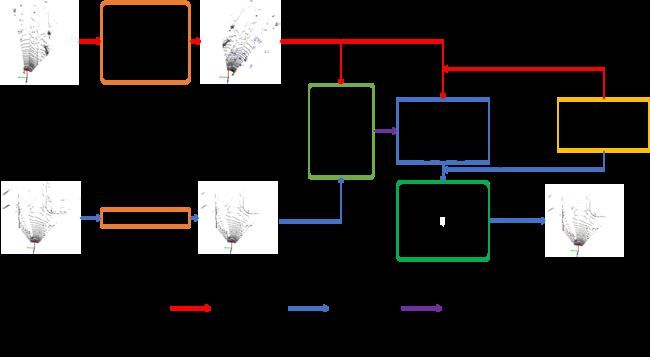
基于Lidar的object检测模型包括Point-based [PointRCNN(CVPR19), IA-SSD(CVPR22)等], Voxel-based [PointPillars(CVPR19), CenterPoint(CVPR21)等]，Point-Voxel-based [PV-RCNN(CVPR20), HVPR(CVPR21)等]和Multi-view-based[PIXOR(CVPR18)等]等。本博客主要记录，作为菜鸟的我，在KITTI数据集上(3类)基于PyTorch实现PointPillars的一些学习心得, 训练和测试的pipeline如Figure 1所示。这里按照深度学习算法的流程进行展开: 数据 + 网络结构 + 预测/可视化 + 评估，和实现的代码结构是一一对应的，完整代码已更新于github: https://github.com/zhulf0804/PointPillars。

[说明 - 代码的实现是通过阅读mmdet3dv0.18.1源码, 加上自己的理解完成的。因为不会写cuda, 所以cuda代码和少量代码是从mmdet3dv0.18.1复制过来的。]

一、KITTI 3D检测数据集

1.1 数据集信息:

• KITTI数据集论文: Are we ready for autonomous driving? the kitti vision benchmark suite [CVPR 2012] 和 Vision meets robotics: The kitti dataset [IJRR 2013]
• KITTI数据集下载(下载前需要登录): point cloud(velodyne, 29GB), images(image_2, 12 GB), calibration files(calib, 16 MB)和labels(label_2, 5 MB)。数据velodyne, calib 和 label_2的读取详见utils/io.py。

1.2 ground truth label信息 [file]

对每一帧点云数据, label是$n$个15维的向量, 组成了8个维度的信息。

	含义	样例
0	类别名称(type)	Car
1	截断(truncated, float)	从 0 (non-truncated) 到 1 (truncated)
2	遮挡(occluded, int)	0=fully visible, 2 = largely occluded
3	观测角(alpha)	$[-\pi ,\pi ]$
4:8	图像2d bbox	(57.68 178.66 341.72 285.91)
8:11	3d 尺寸(dimensions) (h, w, l)	(1.65 1.68 3.88)
11:14	相机坐标系下的坐标(location) (x, y, z), 下平面中心点的坐标	(-6.88 1.77 12.36)
14	相机坐标系下绕$Y$轴旋转的弧度(rotation_y)	[$-\pi ,\pi$]

• 训练时主要用到的是类别信息(type) 和3d bbox 信息 (location, dimension, rotation_y).
• 观测角(alpha)和旋转角(rotation_y)的区别和联系可以参考博客https://blog.csdn.net/qq_16137569/article/details/118873033。

1.3 坐标系的变换

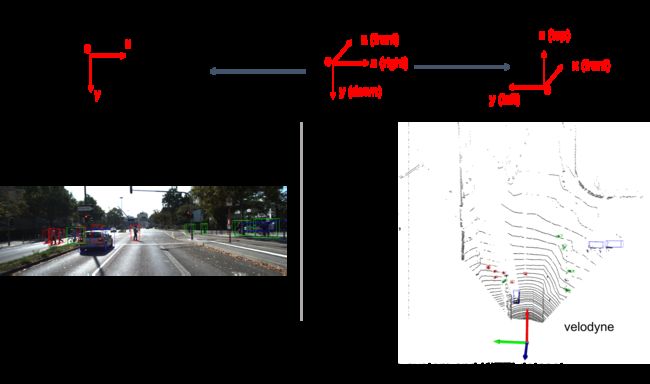
因为gt label中提供的bbox信息是Camera坐标系的，因此在训练时需要使用外参等将其转换到Lidar坐标系; 有时想要把3d bbox映射到图像中的2d bbox方便可视化，此时需要内参。具体转换关系如Figure 2。坐标系转换的代码见utils/process.py。

1.4 数据增强

数据增强应该是Lidar检测中很重要的一环。发现其与2D检测中的增强差别较大，比如3D中会做database sampling(我理解的是把gt bbox进行cut-paste), 会做碰撞检测等。在本库中主要使用了采用了5种数据增强, 相关代码在dataset/data_aug.py。

• 采样gt bbox并将其复制到当前帧的点云
  • 从Car, Pedestrian, Cyclist的database数据集中随机采集一定数量的bbox及inside points, 使每类bboxes的数量分别达到15, 10, 10.
  • 将这些采样的bboxes进行碰撞检测, 通过碰撞检测的bboxes和对应labels加到gt_bboxes_3d, gt_labels
  • 把位于这些采样bboxes内点删除掉, 替换成bboxes内部的点.
• bbox 随机旋转平移
  • 以某个bbox为例, 随机产生num_try个平移向量t和旋转角度r, 旋转角度可以转成旋转矩阵(mat).
  • 对bbox进行旋转和平移, 找到num_try中第一个通过碰撞测试的平移向量t和旋转角度r(mat).
  • 对bbox内部的点进行旋转和平移.
  • 对bbox进行旋转和平移.
• 随机水平翻转
  • points水平翻转
  • bboxes水平翻转
• 整体旋转/平移/缩放
  • object旋转, 缩放和平移
  • point旋转, 缩放和平移
• 对points进行shuffle: 打乱点云数据中points的顺序。

Figure3是对上述前4种数据增强的可视化结果。

二、网络结构与训练

对于输入点云$\mathbf{X}\in {\mathbb{R}}^{N\times 4}$, PointPillars是如何一步步地得到bbox的呢 ? 相关代码见model/pointpillars.py。

2.1 网络结构

• PillarLayer

  Lidar的range是[0, -39.68, -3, 69.12, 39.68, 1], 即(xmin, ymin, zmin, xmax, ymax, zmax)。

  • 基于预先设定好的voxel_size=(0.16, 0.16, 4), 将点云$\mathbf{X}$中的$N$个点划分到(432, 496, 1)个Pillars里。
  • 选择$P$(训练集中最多16000, 测试集中最多40000)个Pillars, 并且每个Pillar选择$M=32$个点, 不足32个点时补(0, 0, 0, 0)。

  数据shape的变化: $(N,4)$ -> $(P,M,4)$, 同时记录这$P$个Pillars在(432, 496)的map中的位置(coors)和每个Pillar中有效点的数量(npoints_per_pillar)。

• PillarEncoder

  • 对每个Pillar中的点进行去均值编码: $(P,M,4)$ -> $$(P, M, 3)
  • 对每个Pillar中有效点进行去中心编码: $(P,M,4)$ -> $(P,M,2)$
  • 合并编码: 将原始的$(P,M,4)$同去均值编码和去中心编码的结果进行cat, 得到$(P,M,9)$的向量。这里有两点需要注意: (1)每个Pillar中只对有效点(npoints_per_pillar)进行操作, 即(0, 0, 0, 0)还是保持(0, 0, 0, 0); (2)这应该是一个trick, 把9维编码向量中的前2维换成去中心编码的向量, 详情见https://github.com/open-mmlab/mmdetection3d/issues/1150。
  • 进行embedding(卷积核池化): $(P,M,9)$ -> $(P,M,64)$ -> $(P,64)$。
  • Pillar scatter: 根据Pillars在map中的位置(coors), 将$P$个pillars的特征scatter到(432, 496)的特征图上(没有Pillar的位置补0向量), 得到$(64,496,432)$的特征图, 这里不妨记为$(C,H,W)$。

  数据shape的变化: $(P,M,4)$ -> $(C,H,W)$。

• Backbone

  在得到了$(C,H,W)$的特征图后, Backbone及接下来的Neck, Head都是在2D上进行操作了，基本是Conv2d + BN + ReLU的组合，所以接下来主要介绍tensor的shape变化。

  • block1: $(C,H,W)$ -> $(C,H/2,W/2)$, 即 $$ -(64, 496, 432)> $(64,248,216)$。
  • block2: $(C,H/2,W/2)$ -> $(2\ast C,H/4,W/4)$, 即 $(64,248,216)$ -> $(128,124,108)$。
  • block3: $(2\ast C,H/4,W/4)$ -> $(4\ast C,H/8,W/8)$, 即 $(128,124,108)$ -> $(256,62,54)$。

  数据shape的变化: $(C,H,W)$ -> $[(C,H/2,W/2),(2\ast C,H/4,W/4),(4\ast C,H/8,W/8)]$。

• Neck

  • decoder1: $(C,H/2,W/2)$ -> $(2\ast C,H/2,W/2)$。
  • decoder2: $(2\ast C,H/4,W/4)$ -> $(2\ast C,H/2,W/2)$。
  • decoder3: $(4\ast C,H/8,W/8)$ -> $(2\ast C,H/2,W/2)$。
  • cat: $$ -[(2C, H/2, W/2), (2C, H/2, W/2), (2*C, H/2, W/2)]> $(6\ast C,H/2,W/2)$。此时，得到的特征图为 $(384,248,216)$。

  数据shape的变化: $[(C,H/2,W/2),(2\ast C,H/4,W/4),(4\ast C,H/8,W/8)]$ -> $(6\ast C,H/2,W/2)$。

• Head

  PointPillars共有3个不同尺寸的anchors(详情见2.2小节), 每个尺寸的anchor有2个角度, 因此共有6个anchors。网络训练了3个类别: Pedestrian, Cyclist和Car。

  • 类别分类branch: $(6\ast C,H/2,W/2)$ -> $(6\ast 3,H/2,W/2)$, 即$(384,248,216)$ -> $(18,248,216)$。
  • bbox回归branch: $(6\ast C,H/2,W/2)$ -> $(6\ast 7,H/2,W/2)$, 即$(384,248,216)$ -> $(42,248,216)$。
  • 朝向分类branch: $(6\ast C,H/2,W/2)$ -> $(6\ast 2,H/2,W/2)$, 即$(384,248,216)$ -> $(12,248,216)$。

  数据shape的变化: $(6\ast C,H/2,W/2)$ -> $[(6\ast 3,H/2,W/2),(6\ast 7,H/2,W/2),(6\ast 2,H/2,W/2)]$。

2.2 GT值生成

Head的3个分支基于anchor分别预测了类别, bbox框(相对于anchor的偏移量和尺寸比)和旋转角度的类别, 那么在训练时, 如何得到每一个anchor对应的GT值呢 ? 相关代码见model/anchors.py

• Anchor生成

  针对3个不同的类别, anchor共包含预先设置了3个尺寸: [0.6, 0.8, 1.73], [0.6, 1.76, 1.73] 和 [1.6, 3.9, 1.56], 2个旋转弧度: 0和$\frac{\pi }{2}$。在尺寸为$(H/2,W/2)$的特征图上每一个位置上放置3*2个anchors, 因此得到shape为$$(H/2,W/2,3,2,7)的anchortensor,即anchortensor的shape为$$(248, 216, 3, 2, 7)。

• Anchors和Gt_bboxes的对应

  这里以尺寸为[0.6, 0.8, 1.73]的anchor为例, 首先将$n$个gt_bboxes与$248\ast 216\ast 2$个anchors进行iou的计算, 并依次划分正负anchors:

  • 正anchor: (1) 如果anchor与所有的gt_bboxes中的最大iou大于pos_iou_thr(0.5), 那么此anchor为正anchor, 且此anchor负责与其有最大iou的gt_bbox (类别, bbox框, 旋转角度的类别); (2) 对每一个gt_bbox, 选择与其有最大iou的anchor, 如果其iou大于min_iou_thr(0.35), 那么此anchor为正anchor, 且此anchor对该gt_bbox负责(类别, bbox框, 旋转角度的类别)。
  • 负anchor: 如果anchor与所有的gt_bboxes中最大iou小于neg_iou_thr(0.35), 那么此anchor为负anchor。

  除了正anchors和负anchors外, 其实还有一些不属于两者的anchors, 即与gt_bboxes的最大iou在0.35-0.5中间的anchors。这里对某一个样本进行了统计, 直观的看一下不同anchors之间的比例: (正anchors, 负anchors, 其它anchors) = (23， 107083， 30)。可以看到: 大部分都是负anchors, 且正负anchors的比例相差很大(后面可以看到focal loss在这里发挥的巨大作用了)。

  另外, 尺寸为[0.6, 1.76, 1.73]的anchor: pos_iou_thr=0.5, neg_iou_thr=0.35, min_iou_thr=0.35; 尺寸为[1.6, 3.9, 1.56]的anchor: pos_iou_thr=0.6, neg_iou_thr=0.45, min_iou_thr=0.45。

• Head输出的GT值

  经过Anchors和Gt_bboxes的对应, 我们知道哪些是正anchors, 哪些是负anchors; 并且知道正anchor与哪个gt_bbox对应。

  • 类别分类: 正负anchors参与类别分类的监督。 此处的输出是3个sigmoid的结果, 即该anchor是第0, 1, 2类的置信度。负anchor的GT值是(0, 0, 0)。正anchor的GT值是(0, 0, 1)或(0, 1, 0)或(1, 0, 0)。

  • bbox回归: 正anchors参与bbox回归的监督。

    对于anchor $(x^a,y^a,z^a,w^a,l^a,h^a,{\theta }^a)$和其对应的gt_bbox $(x^{gt},y^{gt},z^{gt},w^{gt},l^{gt},h^{gt},{\theta }^{gt})$, 模型预测的gt bbox与anchor的位置偏移量和尺寸比:

    $$\begin{gathered} \Delta x=\frac{x^{gt}-x^a}{d^a},\Delta y=\frac{y^{gt}-y^a}{d^a},\Delta z=\frac{z^{gt}-z^a}{h^a}, \\ \Delta w=\log \frac{w^{gt}}{w^a},\Delta l=\log \frac{l^{gt}}{l^a},\Delta h=\log \frac{h^{gt}}{h^a}, \\ \Delta \theta =\sin ({\theta }^{gt}-{\theta }^a), \end{gathered}$$

    其中$d^a=\sqrt{((w^a{)}^2+(l^a{)}^2)}$。

  • 朝向分类: 正anchors参与角度分类的监督。 若anchor对应的gt_bbox的角度在$[0,\pi ]$, 则label为0; 若anchor对应的gt_bbox的角度在$[\pi ,2\ast \pi )$, 则label为1。需要朝向分类是因为, 如果两个车的朝向相差180°, 那么$\sin ({\theta }^{gt}-{\theta }^a)=\sin (({\theta }^{gt}+\pi )-{\theta }^a)$, 即回归的$\Delta \theta$是相同的, 因为不能区分车的朝向。

2.3 损失函数和训练

现在知道了类别分类head, bbox回归head和朝向分类head的预测值和GT值, 接下来介绍损失函数。相关代码见loss/loss.py。

• 类别分类loss: Focal Loss

  $$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$

  $${\alpha }_t=\{\begin{array}{c}\alpha ,y=1,\\ 1-\alpha ,y=0.\end{array},p_t=\{\begin{array}{c}p,y=1,\\ 1-p,y=0.\end{array}$$

  其中$\alpha =0.25,\gamma =2.0$。

  前面提到正负anchors的数量极不平衡, 我在这里测试了一下Focal Loss对于分类loss的影响(batch_size=6)。如下表所示, 经过了Focal Loss (FL), 完全逆转了正负anchors在分类loss中发挥的作用。太强了。这里有一篇博客介绍Focal Loss很详细: https://zhuanlan.zhihu.com/p/82148525。

  	# 正anchors	# 负anchors	正anchors Loss	负anchors Loss
  wo. FL	938	5780509	4416.1719	58345.1328
  w. FL	938	5780509	1083.7280	4.7090

• 回归loss: SmoothL1 Loss

  $$L(x_n,y_n)=\{\begin{array}{c}0.5(x_n-y_n{)}^2/\beta ,|x_n-y_n|<\beta ,\\ |x_n-y_n|-0.5\beta ,\text{otherwise}.\end{array}$$

  这里 $\beta =\frac{1}{9}$。

• 朝向分类loss: Cross Entropy Loss

  $$L(y,\hat{y})=-\sum _{i=1}^n{\hat{y}}_i\log y_i$$

总loss = 1.0*类别分类loss + 2.0*回归loss + 2.0*朝向分类loss。

模型训练: 优化器torch.optim.AdamW(), 学习率的调整torch.optim.lr_scheduler.OneCycleLR(); 模型共训练160epoches。

三、单帧预测和可视化

基于Head的预测值和anchors, 如何得到最后的候选框呢 ? 相关代码见model/pointpillars.py。一般经过以下几个步骤:

1. 基于预测的类别分数的scores, 选出nms_pre (100) 个anchors: 每一个anchor具有3个scores, 分别对应属于每一类的概率, 这里选择这3个scores中最大值作为该anchor的score; 根据每个anchor的score降序排序, 选择anchors。

2. 根据选择的anchors和对其预测的bbox回归值, 解码成bboxes: 以某个anchor$(x^a,y^a,z^a,w^a,l^a,h^a,{\theta }^a)$和预测值$(\Delta x,\Delta y,\Delta z,\Delta w,\Delta l,\Delta h,\Delta \theta )$为例:
   $$\begin{gathered} x^p=\Delta x\cdot d^a+x^a,y^p=\Delta y\cdot d^a+y^a,z^p=\Delta z\cdot h^a+z^a, \\ {w}^p=w^a\cdot e^{\Delta w},l^p=l^a\cdot e^{\Delta l},h^p=h^a\cdot e^{\Delta h},{\theta }^p=\Delta \theta +{\theta }^a \end{gathered}$$

3. 逐类进行以下操作:

• 过滤掉类别score 小于 score_thr (0.1) 的bboxes
• 基于nms_thr (0.01), nms过滤掉重叠框:
  1. 根据score对bboxes从高到低进行排序, 设bboxes集合为$\mathbf{B}$;
  2. 建立空的bboxes集合 $\mathbf{D}$;
  3. 选择score最高的bbox $\mathbf{b}$加入到$\mathbf{D}$;
  4. 计算$\mathbf{B}$中剩余bboxes与$\mathbf{b}$的iou, 过滤掉$\mathbf{B}$中iou大于nms_thr的bboxes;
  5. 重复3, 4, 直到$\mathbf{B}$为空集。
• 根据朝向分类的结果对${\theta }^p$进行矫正:
  • 若朝向分类的结果是0, 则将${\theta }^p$调整到$[0,\pi ]$;
  • 若朝向分类的结果是1, 则将${\theta }^p$调整到$[-\pi ,0]$。

4. 过滤更多的框: 为了避免剩余bboxes仍然过多, 超过max_num (50), 又根据分类score值, 选择出了top max_num个bboxes。

5. 根据Image size和Lidar range过滤bboxes:

• Image size 过滤 (可选): 若知道Lidar对应的image size和相对应的内/外参信息等, 则将3d bbox的顶点映射到2d image, 如果在2d的这些顶点仍然包含在image里, 则保存该bbox; 否则, 过滤掉该bbox。
• Lidar range 过滤: 选择$(x,y,z)$在Lidar range ([0, -40, -3, 70.4, 40, 0.0]) 的bboxes。

至此, 完成了单帧点云的预测过程: 输入是$\mathbf{X}\in {\mathbb{R}}^{N\times c}(c=4)$, 输出是n个bboxes: Lidar_bboxes $\in R^{n\times 7}$, Labels $\in R^{n\times 1}$ 和 Scores $\in R^{n\times 1}$。

另外, 基于Open3d实现了在Lidar和Image里3d bboxes的可视化, 相关代码见test.py和utils/vis_o3d.py。下图是对验证集中id=000134的数据进行可视化的结果。

四、模型评估

评估指标同2D检测类似, 也是采用AP, 即Precison-Recall曲线下的面积。不同的是, 在3D中可以计算3D bbox, BEV bbox 和 (2D bbox, AOS)的AP。

先说明一下AOS指标和Difficulty的定义。

AOS(average orientation similarity): $\frac{1+\cos ({\alpha }^{gt}-{\alpha }^p)}{2}$, 用于评估朝向, 常于2D Bbox一块评估(因为2D Bbox在评估时是基于axis-aligned的bbox的)。

Difficulty: 根据2d框的高度, 遮挡程度和截断程度, 把bbox分为 difficulty=0, 1, 2 或 其它。相关定义具体查看代码pre_process_kitti.py#L16-32。

这里以3D bbox为例, 介绍类别=Car, difficulty=1 AP的计算。注意, difficulty=1的数据实际上是指difficulty<=1的数据; 另外这里主要介绍大致步骤, 具体实现见evaluate.py。

1. 计算3D IoU (utils/process.py iou3d(bboxes1, bboxes2)), 用于判定一个det bbox是否和gt bbox匹配上 (IoU > 0.7)。

2. 根据类别=Car, difficulty=1选择gt bboxes和det bboxes。

• gt bboxes: 选择类别=Car, difficulty<=1的bboxes;
• det bboxes: 选择预测类别=Car的bboxes。

3. 确定P-R曲线中的点对(Pi, Ri)对应的score阈值。

• 建立空的scores集合$\mathbf{S}$;
• 对于每一个gt bbox ${\mathbf{g}}_{\mathbf{b}}$, 选择未被匹配的且与其IoU>0.7中最大的det bbox ${\mathbf{d}}_{\mathbf{b}}$作为匹配框, 并将${\mathbf{d}}_{\mathbf{b}}$标识为已被匹配, 且将${\mathbf{d}}_{\mathbf{b}}$的预测score加入到集合$\mathbf{S}$中; 若没有满足条件的${\mathbf{d}}_{\mathbf{b}}$, 则无需将${\mathbf{d}}_{\mathbf{b}}$的预测score加入到集合$\mathbf{S}$中;
• 对集合$\mathbf{S}$中scores进行由高到低排序;
• 计算gt bboxes的数量, 根据$\mathbf{S}$计算Recall在0, 1/40, 2/40, …, $|\mathbf S| / |\text{gt bboxes}| $ 的scores, 构成阈值集合${\mathbf{S}}^{\ast }$。

4. PR曲线和AP的计算。

• 针对阈值集合${\mathbf{S}}^{\ast }$中的每一个${\mathbf{s}}_i$, 计算一组(Pi, Ri):

  • 匹配: 对于gt bbox ${\mathbf{g}}_{\mathbf{b}}$, 选择未被匹配的, 预测score >= ${\mathbf{s}}_i$ 且与其IoU>0.7中最大的det bbox ${\mathbf{d}}_{\mathbf{b}}$作为匹配框, 并将${\mathbf{d}}_{\mathbf{b}}$标识为已被匹配;
  • 计算TP: 所有匹配的det bboxes ${\mathbf{d}}_{\mathbf{b}}$的数量; 如果${\mathbf{d}}_{\mathbf{b}}$对应的2D bbox的height不满足difficulty<=1的要求, 则不计入TP。
  • 计算FN: 所有未被匹配的 gt bboxes ${\mathbf{g}}_{\mathbf{b}}$ 的数量; 即使${\mathbf{g}}_{\mathbf{b}}$仅被不满足difficulty<=1要求的${\mathbf{d}}_{\mathbf{b}}$匹配, 仍旧不算FN。
  • 计算FP: 所有未被匹配的预测score >= ${\mathbf{s}}_i$且height满足difficulty<=1的det bboxes的数量; 对于2D Bbox AP的评估, 需要注意的是, 如果${\mathbf{d}}_{\mathbf{b}}$匹配到了Dontcare的gt bboxes, 不算在FP(标注为Dontcare的有些是比较远的, 在2D中可以看到, 但在3D中是不可见的; 因此在2D中进行了标注, 但在3D中未进行标注)。
  • 计算Precision: Pi = TP / (TP + FP), Recall: Ri = TP / (TP + FN).

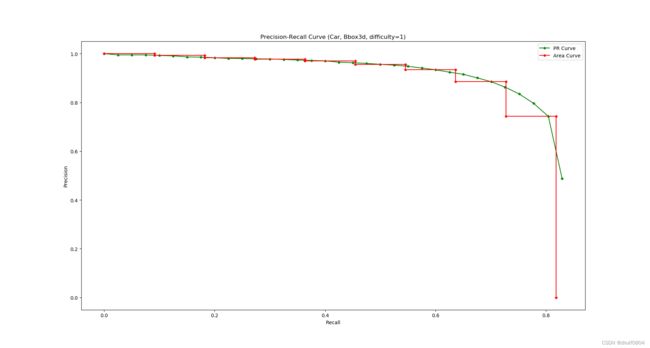
• PR曲线和AP计算

  基于点对(Pi, Ri)绘制曲线如下图绿色曲线所示, 曲线下的面积记为AP。但在实现的时候使用了11 recall positions方式的进行评估, 如下图红色折线所示。

  mAP是求取所有(3个)类别AP的均值。

五、总结

• 点云检测, 相比于点云中其它任务(分类, 分割和配准等), 逻辑和代码都更加复杂, 但这并不是体现在网络结构上, 更多的是体现在数据增强, Anchors和GT生成, 单帧推理等。
• 点云检测, 相比于2D图像检测任务, 不同的是坐标系变换, 数据增强(碰撞检测, 点是否在立方体判断等), 斜长方体框IoU的计算等; 评估方式因为考虑到DontCare, difficulty等, 也更加复杂一些.
• 初次接触基于KITTI的3D检测, 如有理解错误的, 还请指正; 内容太多了, 如有遗漏, 待以后补充。