数据结构——二叉树

二叉树的基本定义

二叉树就是度不超过2的树(每个结点最多有两个子结点)

 

二叉查找树的创建

二叉查找树的API设计

二叉查找树实现步骤

1.插入方法put实现思想

（1）如果当前树没有任何一个结点，则直接把新结点当做根节点使用

（2）如果当前树不为空，则从根节点开始：

1）如果新结点的key小于当前结点的key，则继续找当前结点的左子结点

2）如果新结点的key大于当前结点的key，则继续找当前结点的右子结点

3）如果新结点的key等于当前结点的key，则树中已经存在这样的结点，替换该结点的value值即可

2.查询方法get实现思想

从根节点开始

（1）如果要查询的key小于当前结点的key，则继续寻找当前结点的左子结点

（2）如果要查询的key大于当前结点的key，则继续寻找当前结点的右子结点

（3）如果要查询的key等于当前结点的key，则树中返回当前结点的value值

3.删除方法delete实现思想

（1）找到被删除结点

（2）找到被删除结点右子树中的最小结点minNode

（3）删除右子树中的最小结点

（4）让被删除结点的左子树称为最小结点minNode的左子树，让被删除结点的右子树称为最小结点minNode的右子树

（5）让被删除结点的父节点指向最小结点minNode

二叉查找树的代码实现

public class BinaryTree,Value> {
    //记录根节点
    private Node root;
    //记录树中元素的个数
    private int N;
    private class Node{
        private Key key;
        private Value value;
        private Node left;
        private Node right;
        public Node(Key key,Value value,Node left,Node right){
            this.key=key;
            this.value=value;
            this.left=left;
            this.right=right;
        }
    }
    //获取树中元素的个数
    public int size(){
        return N;
    }
    //向树中插入一个键值对
    public void put(Key key,Value value){
         root = put(root, key, value);
    }
    //给指定树x上，添加一个键值对，并返回添加后的新树
    public Node put(Node x,Key key,Value value){
        //当前树没有结点，就把新结点当做是根节点
        if(x==null){
            x=new Node(key,value,null,null);
            N++;
            return x;
        }
        int cmp=key.compareTo(x.key);
        //新结点的key大于当前结点，继续寻找当前结点的右子结点
        if(cmp>0){
            x.right=put(x.right,key,value);
        }else if(cmp<0){
            //新结点的key小于当前结点，继续寻找当前结点的左子结点
            x.left=put(x.left,key,value);
        }else{
            //新结点的key等于当前结点，替换当前结点的value值
            x.value=value;
        }
        return x;
    }
    //根据key，从树中找到对应的值
    public Value get(Key key){
        return get(root,key);
    }
    //从指定的树x中，找到key对应的值
    public Value get(Node x,Key key){
          if(x==null){
              return null;
          }
          int cmp=key.compareTo(x.key);
          if(cmp>0){
              //新结点的key大于当前结点，继续寻找当前结点的右子结点
              return get(x.right,key);
          }else if(cmp<0){
              //新结点的key小于当前结点，继续寻找当前结点的左子结点
               return get(x.left,key);
          }else{
              //新结点的key等于当前结点，返回当前结点的value值
              return x.value;
          }
    }
    //根据key，删除树中对应的键值对
    public void delete(Key key){
        root=delete(root,key);
    }
    //删除指定树x上的键为key的键值对，并返回删除后的新树
    public Node delete(Node x,Key key){
         if(x==null){
             return null;
         }
        int cmp=key.compareTo(x.key);
         if(cmp>0){
             //新结点的key大于当前结点，继续寻找当前结点的右子结点
             x.right=delete(x.right,key);
         }else if(cmp<0){
             //新结点的key小于当前结点，继续寻找当前结点的左子结点
             x.left=delete(x.left,key);
         }else{
             //新结点的key等于当前结点
             //让元素个数-1
             N--;
             //1.如果当前结点的右子树不存在，则直接返回当前结点的左子节点
             if(x.right==null){
                 return x.left;
             }
             //2.如果当前结点的左子树不存在，则直接返回当前结点的右子结点
             if(x.left==null){
                 return x.right;
             }
             //3.当前结点的左右子树都存在,要删除的结点就是x
             //3.1找到右子树中最小的结点
             Node minNode=x.right;
             while(minNode!=null){
                 minNode=minNode.left;
             }
             //3.2删除右子树中最小的结点
             Node n=x.right;
             while (n.left!=null){
                 if(n.left.left==null){
                     n.left=null;
                 }else{
                     n=n.left;
                 }
             }
             //3.3让被删除结点的左子树称为最小结点的左子树，让被删除结点的右子树成为最小结点的右子树
             minNode.left=x.left;
             minNode.right=x.right;
             //3.4让被删除结点的父节点指向最小结点
             x=minNode;
         }
         return x;
    }
}

//测试代码
public class BinaryTreeTest {
    public static void main(String[] args){
        BinaryTree bt=new BinaryTree<>();
        bt.put(2,"aaa");
        bt.put(1,"1222");
        bt.put(4,"ddd");
        bt.put(32,"qw");
        System.out.println(bt.size());
        bt.put(1,"qqqq");
        System.out.println(bt.size());
        System.out.println(bt.get(1));
        bt.delete(1);
        System.out.println(bt.size());
    }
}

二叉查找树中查找最小的键和最大的键

   //找出树中最小的键
    public Key min(){
        return min(root).key;
    }
    //找出指定树x中，最小键所在的结点
    public Node min(Node x){
        if(x.left!=null){
            return min(x.left);
        }else{
            return x;
        }
    }
    //找出树中最大的键
    public Key max(){
        return max(root).key;
    }
    //找出指定树x中，最大键所在的结点
    public Node max(Node x){
        if(x.right!=null){
            return max(x.right);
        }else{
            return x;
        }
    }

二叉树的基础遍历

可以把二叉树的遍历分为以下三种方式：
1.前序遍历：先访问根结点，然后再访问左子树，最后访问右子树
2.中序遍历：先访问左子树，中间访问根节点，最后访问右子树
3.后序遍历：先访问左子树，再访问右子树，最后访问根节点

前序遍历

实现步骤

1.把当前结点的key放入到队列中
2.找到当前结点的左子树，如果不为空，递归遍历左子树
3.找到当前结点的右子树，如果不为空，递归遍历右子树

代码实现

 //使用前序遍历，获取整个树中所有的键
    public Queue preErgodic(){
        Queue keys=new LinkedList<>();
        preErgodic(root,keys);
        return keys;
    }
    //使用前序遍历，把指定树x中的所有键放入keys队列中
    public void preErgodic(Node x,Queue keys){
        if(x==null){
            return;
        }
        //1.把当前结点的key放入队列中
        keys.offer(x.key);
        //2.找到当前结点的左子树，如果不为空，递归遍历左子树
        if(x.left!=null){
            preErgodic(x.left,keys);
        }
        //3.找到当前结点的右子树，如果不为空，递归遍历右子树
        if(x.right!=null){
            preErgodic(x.right,keys);
        }
    }

//测试代码
public class PreTest {
    public static void main(String[] args){
        BinaryTree bt=new BinaryTree<>();
        bt.put("E","5");
        bt.put("B","2");
        bt.put("G","7");
        bt.put("A","1");
        bt.put("D","4");
        bt.put("F","6");
        bt.put("H","8");
        bt.put("C","3");
        Queue queue = bt.preErgodic();
        for(String q:queue){
            System.out.println(q);
        }
    }
}

中序遍历

实现步骤

1.找到当前结点的左子树，如果不为空，递归遍历左子树
2.把当前结点的key放入到队列中
3.找到当前结点的右子树，如果不为空，递归遍历右子树

代码实现

   //使用中序遍历，获取整个树中所有的键
    public Queue midErgodic(){
        Queue keys=new LinkedList<>();
        midErgodic(root,keys);
        return keys;
    }
    //使用中序遍历，把指定树x中的所有键放入keys队列中
    public void midErgodic(Node x,Queue keys){
        if(x==null){
            return;
       }
        //1.找到当前结点的左子树，如果不为空，递归遍历左子树
        if(x.left!=null){
            midErgodic(x.left,keys);
        }
        //2.把当前结点的key放入队列中
        keys.offer(x.key);
        //3.找到当前结点的右子树，如果不为空，递归遍历右子树
        if(x.right!=null){
            midErgodic(x.right,keys);
        }
    }

后序遍历

实现步骤

1.找到当前结点的左子树，如果不为空，递归遍历左子树
2.找到当前结点的右子树，如果不为空，递归遍历右子树
3.把当前结点的key放入到队列中

代码实现

 //使用后序遍历，获取整个树中所有的键
    public Queue afterErgodic(){
        Queue keys=new LinkedList<>();
        afterErgodic(root,keys);
        return keys;
    }
    //使用后序遍历，把指定树x中的所有键放入keys队列中
    public void afterErgodic(Node x,Queue keys){
        if(x==null){
            return;
        }
        //1.找到当前结点的左子树，如果不为空，递归遍历左子树
        if(x.left!=null){
            afterErgodic(x.left,keys);
        }
        //2.找到当前结点的右子树，如果不为空，递归遍历右子树
        if(x.right!=null){
            afterErgodic(x.right,keys);
        }
        //3.把当前结点的key放入队列中
        keys.offer(x.key);
    }

二叉树的层序遍历

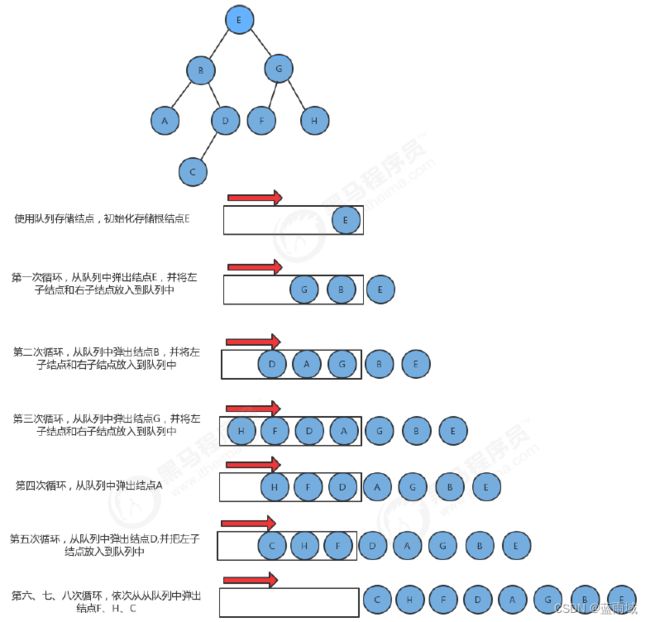
层序遍历，就是从根节点（第一层）开始，依次向下，获取每一层所有结点的值

实现步骤

1.创建队列，存储每一层的结点
2.使用循环从队列中弹出一个结点
2.1获取当前结点的key
2.2如果当前结点的左子结点不为空，则把左子结点放入到队列中
2.3如果当前结点的右子结点不为空，则把右子结点放入到队列中

代码实现

 //层序遍历
    public Queue layerErgodic(){
        //1.创建两个队列，分别存储结点和key
        Queue nQueue=new LinkedList<>();
        Queue kQueue=new LinkedList<>();
        nQueue.offer(root);
        //2.使用循环从队列中弹出结点
        while(!nQueue.isEmpty()){
            Node x = nQueue.poll();
            //2.1获取当前结点的key
            kQueue.offer(x.key);
            //2.2如果当前结点的左子结点不为空，则把左子节点放入队列中
            if(x.left!=null){
                nQueue.offer(x.left);
            }
            //2.3如果当前结点的右子节点不为空，则把右子节点放入队列中
            if(x.right!=null){
                nQueue.offer(x.right);
            }
        }
        return kQueue;
    }

 二叉树的应用

最大深度问题

需求

给定一棵树，请计算树的最大深度（树的根节点到最远叶子结点的最长路径上的结点数）

实现步骤

1.如果根结点为空，则最大深度为0
2.计算左子树的最大深度
3.计算右子树的最大深度
4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1

代码实现

 //计算整个树的最大深度
    public int maxDepth(){
        return maxDepth(root);
    }
    //计算指定树x的最大深度
    public int maxDepth(Node x){
        if(x==null){
            return 0;
        }
        int maxL=0;
        int maxR=0;
        int max=0;
        //1.计算左子树的最大深度
        if(x.left!=null){
            maxL=maxDepth(x.left);
        }
        //2.计算右子树的最大深度
        if(x.right!=null){
            maxR=maxDepth(x.right);
        }
        //3.当前树的最大深度=左子树的最大深度和右子树的最大深度较大者+1
        max=(maxL>maxR)?maxL+1:maxR+1;
        return max;
    }