【机器学习】吴恩达作业7.1，python实现PCA主成分分析

7.1主成分分析

主成分分析（PCA）来实现降维。

首先用一个二维的样本集来实验，对PCA如何运行的有一个直观的感受，然后再在一个更大的由5000个人脸图像组成的数据集上实现PCA。

降噪 ：

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。

降维具有如下一些优点：

• 使得数据集更易使用。
• 降低算法的计算开销。
• 去除噪声。
• 使得结果容易理解。

PCA ：

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
差最小） 

1 压缩数据（减少内存和硬盘的需求/加速算法）
2 可视化数据

线性回归和神经网络算法，都可以先使用PCA对特征进行降维

步骤： 

先将数据进行均值归一化（mean normalization），然后找到一个低维平面，将数据投影到上面，使得投影误差（projection error）最小（即找到一组基向量，然后将数据投影到这个向量空间里，使得投影误差最小

选择主成分K的数量：

使误差降到最小，使绝大部分方差得以保留

 

 不要用PCA去防止过拟合，可能会丢失一些有价值的信息！
除非原始数据直接建模不好（内存太大或者运行太慢），才使用PCA进行降维处理之后再进行建模，一般建议直接用原始数据进行建模

代码 ：

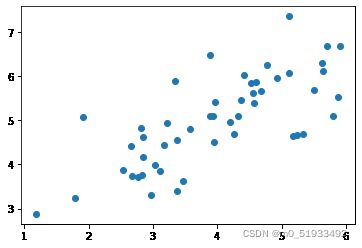
1 导入数据及可视化 

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio

data = sio.loadmat('ex7data1')
data
X = data['X']
X.shape#(50, 2)
data.keys()#dict_keys(['__header__', '__version__', '__globals__', 'X'])

plt.scatter(X[:,0],X[:,1])
plt.show

 

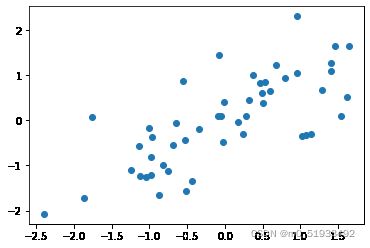
 2 对数据标准化，可视化

#对X标准化

def demean(X):
# X_demean = X - np.mean(X,axis = 0)#对纵轴求均值
    mu = X.mean(axis=0) #求每列的
    sigma = X.std(axis=0, ddof=1) #无偏的标准差，自由度为n-1
    X = (X-mu)/sigma
    return X, mu, sigma

X_demean, mu, sigma = demean(X)

plt.scatter(X_demean[:,0],X_demean[:,1])
plt.show

 3 计算协方差及特征向量

比较两个不同的特征向量（第1列和第2列）哪个投影误差更小，画出以数据均值为中心的特征向量，取U矩阵中第1列得到矩阵（[-0.70710678, -0.70710678]）

#得到协方差和特征向量U
def pca(x):
    m = len(X)
    C = (x.T @ x)/m #计算协方差矩阵  主对角线上是X的方差，副对角线是X的协方差
    U, S, V = np.linalg.svd(C) #SVD奇异值分解计算特征向量U
    return U, S

U, S = pca(X_demean)

#U1 = U[:,0]#取特征向量中第一列矩阵
#U1.shape #(2,)

#画出特征向量
plt.figure(figsize=(6,6))
plt.scatter(X[:,0], X[:,1], marker='o', facecolors='none', edgecolors='b')
plt.plot([mu[0], mu[0]+1.5*S[0]*U[0,0]], [mu[1], mu[1]+1.5*S[0]*U[1,0]], 'k') #两个点的连线
plt.plot([mu[0], mu[0]+1.5*S[1]*U[0,1]], [mu[1], mu[1]+1.5*S[1]*U[1,1]], 'k') #这里的1.5和S表示特征向量的长度
plt.title('Computed eigenvectors of the dataset')

 4 将均值化后的数据投影到特征向量上，实现降维

#降维，将均值化后的数据投影到特征向量上
def X_reduction(x, U, K):
    U_reduce = U[:, 0:K]#选择特征向量矩阵的前K列  
    return X @ U_reduce
    
#降维(50, 1)
z = X_reduction(X_demean, U, 1)#K取1
z[0] #1.48127391

5 重建数据，得到数据的近似值

#重建降维后的数据
def recoverData(z, U, K):
    U_reduce = U[:, 0:K]
    return z @ U_reduce.T #U是特征向量矩阵，由标准正交基组成，U.T@U为单位矩阵

#重建后的数据
X_restore = recoverData(z, U, 1)
X_restore[0,:] #[-1.04741883, -1.04741883]

6  可视化投影，画出标准化数据以及投影（降维）后又重建的数据，对应点用虚线连接

#可视化投影
plt.scatter(X[:,0],X[:,1],marker='o', facecolors='none', edgecolors='b')
plt.scatter(X_restore[:,0],X_restore[:,1],marker='o', facecolors='none', edgecolors='r')
for i in range(len(X)):
    plt.plot([X[i,0], X_restore[i,0]], [X[i,1], X_restore[i,1]], 'k--')
plt.title('The normalized and projected data after PCA')
plt.show()

 

 7 查看降维后的数据保留了原始数据多少差异性

# 查看保留差异
def retained_variance(S, K):
    rv = np.sum(S[:K])/np.sum(S)
    return print('{:.2f}%'.format(rv*100))

retained_variance(S, 1) #86.78%

 案例：使用pca进行图像的降维

mat = sio.loadmat('ex7faces.mat')
mat.keys()
A = mat['X']
A.shape#(5000, 1024)

def plot_100_images(A):
    fig,axs = plt.subplots(ncols = 10,nrows = 10,figsize = (10,10))#定义n*n的子画布(n = 10)
    #在每个子画布中画出一个图像
    for c in range(10):
        for r in range(10):
            axs[c,r].imshow(A[10*c + r].reshape(32,32).T,cmap = 'Greys_r')#显示单通道的灰图
            axs[c,r].set_xticks([])
            axs[c,r].set_yticks([])
plot_100_images(A)     

A_demean  = A - np.mean(A,axis = 0)#A去均值化
C = A_demean.T@A_demean/len(A)#计算协方差
U,S,V = np.linalg.svd(C)#特征值  特征向量
U1 = U[:,:36]
U.shape,U1.shape#((1024, 1024), (1024, 36))

A_reduction = A_demean @ U1#对A进行降维
A_reduction.shape#(5000, 36)

A_recover = A_reduction @ U1.T + np.mean(A,axis = 0)

plot_100_images(A_recover),plot_100_images(A)#原始数据与还原后数据做对比