Opencv的使用小教程3——利用轮廓检测实现二维码定位
Opencv的使用小教程3——利用轮廓检测实现二维码定位
- 二维码具有什么特征
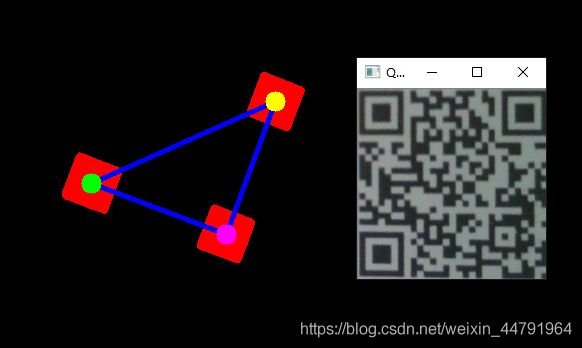
- 实现效果
- 识别二维码的流程
-
- 1、预处理图像
- 2、寻找轮廓
- 3、通过寻找到的轮廓确定“回”的位置
- 4、创建一张新图,并在新图上画出识别到的“回”并连线
- 5、寻找直角
- 6、确定另外两个点的次序关系
- 7、计算旋转角
- 8、完成二维码的旋转
- 全部代码
好好学习噢!
![]()
二维码具有什么特征
二维码就是两个维度的条形码,平常我们在生活中随处可见,“QR”是“Quick Response”的缩写,它指的就是可以对隐藏在二维码中的数据实现快速读取。QR码相对传统条形码的优势是数据存储量大和高容错性。
我们都知道二维码有三个非常明显的黑框,就像下面的图显示的一样。

而这三个框框因为其明显的特征,它的作用也是用于二维码的定位。
因此,要实现二维码的定位,最重要的一点就是定位这三个框框,三个回。
这三个回有什么特点呢?
1、每一个“回”在包括最外边的轮廓的情况下,都存在三个轮廓,分别是:内部黑色正方形轮廓,白色正方形轮廓,外部轮廓。
2、每一个“回”的黑白框框的比例大概为1:3:1:1。
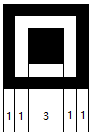
3、左上角的“回”与其它的顶点的夹角为90度
实现效果
识别二维码的流程
在看流程前,可以前往我的github下载源码https://github.com/bubbliiiing/QRcode-location
1、预处理图像
在正式确定二维码的位置之前,首先要对原始图像进行处理,不能让原始图像很随意的直接使用,这其中包括一些重要的步骤:
1、利用cvtColor转化成灰度图像。
2、利用blur平滑图像,去除一些噪点。
3、利用convertScaleAbs实现图像的对比度增强。便于区分特征。
4、利用equalizeHist计算直方图,直方图的作用也是为了使得整个图像的区分度更大。
5、利用threshold阈值操作,将整个图像分为黑白两个极点,便于之后寻找轮廓。
以上所有的步骤都是为了让图像更便于寻找轮廓。
一个彩色的二维码图像,在经过如上的处理之后,可能会得到如下的图像:

2、寻找轮廓
在得到上述图像后,重要的是如何找到三个“回”,根据“回”的特点:每一个“回”在包括最外边的轮廓的情况下,都存在三个轮廓,分别是:内部黑色正方形轮廓,白色正方形轮廓,外部轮廓,我们可以完成回的寻找。
本文利用opencv自带的findContours函数寻找轮廓。
findContours的调用方式如下:
findContours(srcGray, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE);
其中:
1、srcGray是需要寻找轮廓的图像;
2、contours是寻找到的轮廓的存储变量,其变量类型为vector
3、hierarchy是轮廓之间的关系,其变量类型为vector,每一个hierarchy的元素包括了四个int的数据,分别表示第i个轮廓的后一个轮廓、前一个轮廓、子轮廓、父轮廓的索引编号。
3、通过寻找到的轮廓确定“回”的位置
在这里一部分,又要开始提到“回”的特点,其重要特点为存在三个轮廓,分别是:内部黑色正方形轮廓,白色正方形轮廓,外部轮廓。
如果我们可以找到内部具有两个轮廓的轮廓,大概率就是我们需要的“回”的位置,这里我给标亮了,大家应该看的明白。

我们对所有的轮廓进行判断,其内部是否有两个轮廓。
判断的方式如下,我用伪代码的形式呈现:
# ic用于确定这是“回”字判别中的第几个轮廓
for 轮廓i in 所有轮廓:
if 该轮廓有子轮廓且ic == 0:
保存该轮廓id
ic++
elif 该轮廓是父轮廓:
ic++
elif 该轮廓不是父轮廓:
初始化ic
初始化父轮廓id
if ic == 2:
# 表示总共检测到三个连续的轮廓,满足外轮廓中有两个轮廓的要求
if(IsQrPoint):
# IsQrPoint该函数通过面积二次判断是否为“回”字
保存该轮廓
# 此时已经检测到一个“回"
初始化ic
初始化父轮廓id
该流程执行同样得益于findContours在父轮廓与子轮廓是连续排序的。即父轮廓后一个轮廓是其子轮廓。
具体的执行代码如下:
for (int i = 0; i < contours.size(); i++)
{
// 判断是否为父轮廓
if (hierarchy[i][2] != -1 && ic == 0)
{
parentIdx = i;
ic++;
}
// 判断是否是父轮廓内的子轮廓
else if (hierarchy[i][2] != -1)
{
ic++;
}
else if (hierarchy[i][2] == -1)
{
parentIdx = -1;
ic = 0;
}
// 判断是否积累检测到三个轮廓
if (ic == 2)
{ //通过图像处理进行深层次的判断
if (IsQrPoint(contours[parentIdx], src)) {
RotatedRect rect = minAreaRect(Mat(contours[parentIdx]));
// 画图部分
Point2f points[4];
rect.points(points);
for (int j = 0; j < 4; j++) {
line(src, points[j], points[(j + 1) % 4], Scalar(0, 255, 0), 2);
}
drawContours(canvas, contours, parentIdx, Scalar(0, 0, 255), -1);
// 如果满足条件则存入
center_all.push_back(rect.center);
numOfRec++;
}
ic = 0;
parentIdx = -1;
}
}
4、创建一张新图,并在新图上画出识别到的“回”并连线
该部分的目的主要是在新图上绘画出三个“回”,然后利用findContours得到轮廓,在新图上,一共会获得四个轮廓,分别是三个“回”的轮廓和整个QRcode的轮廓,然后为所有的轮廓利用minAreaRect函数构建最小的矩形,之所以这样做是因为原图干扰太多,直接在新图上构建矩形可以很容易避免干扰,只要识别“回”识别的正确,就一定可以得到正确的矩形。
在该部分需要执行的流程是:
1、利用findContours得到轮廓。
2、利用minAreaRect得到与轮廓最相符合的矩形
3、对矩形面积进行检测筛选,最大面积的矩形就是QRcode的矩形,比较小的三个矩形是“回”
具体执行代码如下
vector<vector<Point>> contours3;
Mat canvasGray;
cvtColor(canvas, canvasGray, COLOR_BGR2GRAY);
findContours(canvasGray, contours3, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
vector<Point> maxContours;
double maxArea = 0;
// 在原图中画出二维码的区域
for (int i = 0; i < contours3.size(); i++)
{
RotatedRect rect = minAreaRect(contours3[i]);
Point2f boxpoint[4];
rect.points(boxpoint);
for (int i = 0; i < 4; i++)
line(src, boxpoint[i], boxpoint[(i + 1) % 4], Scalar(0, 0, 255), 3);
double area = contourArea(contours3[i]);
if (area > maxArea) {
maxContours = contours3[i];
maxArea = area;
}
}
imshow("src", src);
if (numOfRec < 3) {
waitKey(10);
continue;
}
RotatedRect rect = minAreaRect(Mat(maxContours));
5、寻找直角
在上几步中,我们已经获得的了“回”的位置和整个二维码的大概轮廓,这一步,我们主要是对二维码的方向进行矫正,对二维码而言,其三个“回”存在次序关系,左上角的“回”与另外两个“回”构成直角,像这样。

如何确定三个回哪个是直角呢,我们通过向量垂直公式判断:
两个向量垂直,有垂直定理: 若设向量a=(x1,y1),b=(x2,y2) ,a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0。
在此处我们只需要将任意两个“回”的中心坐标相减就可以得到一个“回”到另一个回的向量。
通过如下方式判断:
int leftTopPoint(vector<Point> centerPoint) {
int minIndex = 0;
int multiple = 0;
int minMultiple = 10000;
multiple = (centerPoint[1].x - centerPoint[0].x)*(centerPoint[2].x - centerPoint[0].x) + (centerPoint[1].y - centerPoint[0].y)*(centerPoint[2].y - centerPoint[0].y);
if (minMultiple > multiple){
minIndex = 0;
minMultiple = multiple;
}
multiple = (centerPoint[0].x - centerPoint[1].x)*(centerPoint[2].x - centerPoint[1].x) + (centerPoint[0].y - centerPoint[1].y)*(centerPoint[2].y - centerPoint[1].y);
if (minMultiple > multiple) {
minIndex = 1;
minMultiple = multiple;
}
multiple = (centerPoint[0].x - centerPoint[2].x)*(centerPoint[1].x - centerPoint[2].x) + (centerPoint[0].y - centerPoint[2].y)*(centerPoint[1].y - centerPoint[2].y);
if (minMultiple > multiple) {
minIndex = 2;
minMultiple = multiple;
}
return minIndex;
}
6、确定另外两个点的次序关系
这一步主要是用于确定三个“回”中,除去直角的“回”,另外两个“回"的位置,之所以要确定是因为确定了之后才能完成完成二维码的矫正。
一个摆正的二维码是这样的:
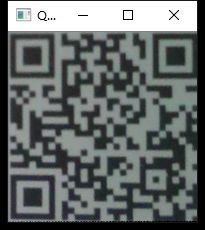
左上角的“回”就是垂直角的“回”,右上角的“回”和左下角的“回”是不可以替换的,我们如果能够确定其次序关系,将有助于我们对二维码进行矫正定位。
如何确定这另外两个“回”的次序呢,在确定直角的时候我们使用了垂直定理,实际上求的是两个向量的内积,现在我们使用外积的公式。
什么是外积呢,大概是这样:
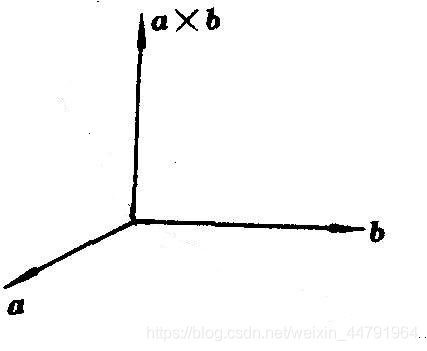
a外积b得到的向量就是朝上的,b外积a得到的向量与之相反,是朝下的。
在二维码上是怎么体现的呢?
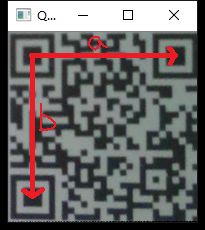
在这里我定义了a、b两条直线,此时a外积b得到的向量就是电脑屏幕朝里的,b外积a得到的向量与之相反,是朝外的。
在实际使用时,我们假设a、b在同一平面,它们的z轴方向的分量都是0,因此他们外积的结果只会与z轴平行,此时我们便可以通过z轴上数值的正负判断两个点的次序了。(这里需要数学基础……我虽然懂但是真的讲不太来。)
具体计算公式如下:
![]()
具体实现代码为,otherIndex[0]就是右上角的“回”,otherIndex[1]就是左下角的“回”:
vector<int> otherTwoPoint(vector<Point> centerPoint,int leftTopPointIndex) {
vector<int> otherIndex;
double waiji = (centerPoint[(leftTopPointIndex + 1) % 3].x- centerPoint[(leftTopPointIndex) % 3].x)*
(centerPoint[(leftTopPointIndex + 2) % 3].y - centerPoint[(leftTopPointIndex) % 3].y) -
(centerPoint[(leftTopPointIndex + 2) % 3].x - centerPoint[(leftTopPointIndex) % 3].x)*
(centerPoint[(leftTopPointIndex + 1) % 3].y - centerPoint[(leftTopPointIndex) % 3].y);
if (waiji > 0) {
otherIndex.push_back((leftTopPointIndex + 1) % 3);
otherIndex.push_back((leftTopPointIndex + 2) % 3);
}
else {
otherIndex.push_back((leftTopPointIndex + 2) % 3);
otherIndex.push_back((leftTopPointIndex + 1) % 3);
}
return otherIndex;
}
7、计算旋转角
计算旋转角需要借助三个“回”的点位来进行。
首先通过如下公式计算右上角的“回”与左上角的“回”形成的k值。
double dy = rightTopPoint.y - leftTopPoint.y;
double dx = rightTopPoint.x - leftTopPoint.x;
double k = dy / dx;
再利用以下公式可以计算对应的与opencv中x轴形成的角度:
double angle = atan(k) * 180 / CV_PI;//转化角度
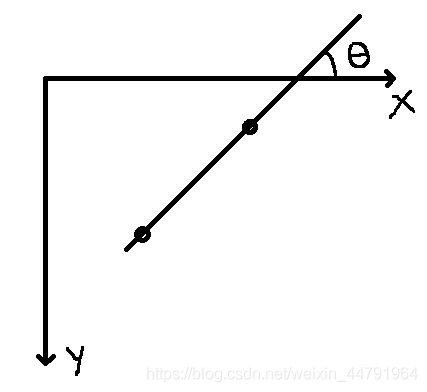
此时θ角是负值。计算出该θ角就可以对图像进行矫正了,但是仅仅使用左上角和右上角可能会存在图像对称的问题,具体情况如下。
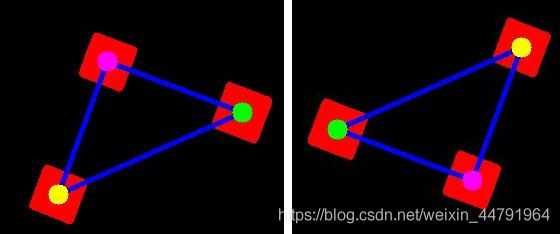
这两幅图的θ角是一样的,但是明显,其需要旋转的角度不同,左边那幅图旋转theta角之后就可以摆正,但是右边那幅图我们会得到如下结果。

很明显,需要再旋转180度才可以得到正确结果,通过对比我们发现,当左下角的“回”的y值小于左上角的“回”的y值时(opencv坐标系),会出现上述情况,因此,我们需要再判断左下角的“回”的y值和左上角的“回”的y值的关系。
if (leftBottomPoint.y < leftTopPoint.y)
angle -= 180;
即可。
最后得到旋转角度的函数为:
double rotateAngle(Point leftTopPoint, Point rightTopPoint, Point leftBottomPoint) {
double dy = rightTopPoint.y - leftTopPoint.y;
double dx = rightTopPoint.x - leftTopPoint.x;
double k = dy / dx;
double angle = atan(k) * 180 / CV_PI;//转化角度
if (leftBottomPoint.y < leftTopPoint.y)
angle -= 180;
return angle;
}
8、完成二维码的旋转
已经得到旋转的角度,之后便可以在原图中获得二维码的旋转结果,并截出二维码区域。
在完成二维码的截取时,需要给二维码截取函数传入三个参数,分别是,原图src,在第四步中得到的包含二维码的矩形rect,旋转的角度angle。
最终处理过程如下:
1、获得旋转中心;
2、获得需要抠图的范围,以旋转中心为中心。
3、通过包含二维码的矩形rect在src中截出尚未旋转的二维码。
4、按旋转中心,利用角度angle完成旋转
5、利用获得的需要抠图的范围进行抠图。
具体处理代码如下:
Mat transformQRcode(Mat src, RotatedRect rect,double angle)
{
// 获得旋转中心
Point center = rect.center;
// 获得左上角和右下角的角点,而且要保证不超出图片范围,用于抠图
Point TopLeft = Point(cvRound(center.x), cvRound(center.y)) - Point(rect.size.height / 2, rect.size.width / 2); //旋转后的目标位置
TopLeft.x = TopLeft.x > src.cols ? src.cols : TopLeft.x;
TopLeft.x = TopLeft.x < 0 ? 0 : TopLeft.x;
TopLeft.y = TopLeft.y > src.rows ? src.rows : TopLeft.y;
TopLeft.y = TopLeft.y < 0 ? 0 : TopLeft.y;
int after_width, after_height;
if (TopLeft.x + rect.size.width > src.cols) {
after_width = src.cols - TopLeft.x - 1;
}
else {
after_width = rect.size.width - 1;
}
if (TopLeft.y + rect.size.height > src.rows) {
after_height = src.rows - TopLeft.y - 1;
}
else {
after_height = rect.size.height - 1;
}
// 获得二维码的位置
Rect RoiRect = Rect(TopLeft.x, TopLeft.y, after_width, after_height);
// dst是被旋转的图片,roi为输出图片,mask为掩模
Mat mask, roi, dst;
Mat image;
// 建立中介图像辅助处理图像
vector<Point> contour;
// 获得矩形的四个点
Point2f points[4];
rect.points(points);
for (int i = 0; i < 4; i++)
contour.push_back(points[i]);
vector<vector<Point>> contours;
contours.push_back(contour);
// 再中介图像中画出轮廓
drawContours(mask, contours, 0, Scalar(255,255,255), -1);
// 通过mask掩膜将src中特定位置的像素拷贝到dst中。
src.copyTo(dst, mask);
// 旋转
Mat M = getRotationMatrix2D(center, angle, 1);
warpAffine(dst, image, M, src.size());
// 截图
roi = image(RoiRect);
return roi;
}
全部代码
这是二维码识别的全部代码,只要正确安装了opencv,都是可以正常运行的,这些代码是我参考了很多的blog和学习了很久的opencv才修改出来的,希望需要的人可以点个赞或者关注hahahah。
#include 如果有不懂的地方欢迎大家询问。