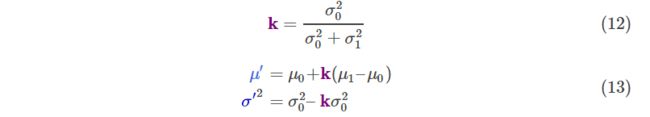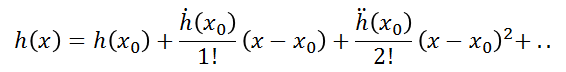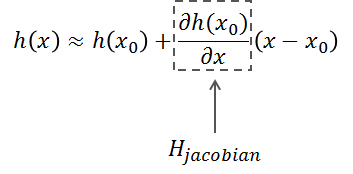v_JULY_v

通俗理解卡尔曼滤波（无人驾驶感知融合的经典算法）

前言

我个人有近10年AI教育经验了，中间获得过一些名号，比如北理工校外导师，微软MVP兼CSDN技术专家，本博客也有1700多万PV了，在AI圈内有极高知名度。后2015年和团队一块创业创办AI职教平台「七月在线」，至今已近7年，这6 7年我们把AI职教做透了，同行没做的我们做，同行没有的广度我们有，同行不到的深度我们到(本处同行仅指AI社会培训机构)。

六年多来，在专注成人AI职教的同时，面对过很多行业的刺激，但自始至终都坚持专注AI。可过程中也越发深刻意识到，AI只有与行业深度结合绑定才能真正发挥出超级价值，考虑到我们的使命始终是“推动社会智能化发展”，加之国家的制造强国战略特别提到新能源汽车、智能汽车，而AI可以很好的赋能自动驾驶，所以一个月前我司平台的定位由“AI职教平台”改为“AI与汽车职教平台”（后最终为：智能时代在线职教平台）。

一个月的时间，我们组织了50位汽车专家/讲师（年底100人），与原有的200+AI专家/讲师区分开，大家讨论中都深感传统车企向智能化转型的急迫。偶然中，在一车企客户现场聊到感知融合的经典算法：卡尔曼滤波（Kalman Filter），故新一篇博客就写这个。这算法神到什么程度呢，比如有人号称当年阿波罗就靠它登陆上的月球 :)

关于卡尔曼滤波，网上有一篇经典文章《How a Kalman filter works, in pictures》，也有不少朋友对它进行过翻译。我看过几遍，觉得还可以把卡尔曼滤波解释的更通俗些，毕竟把相对复杂的算法尽可能解释的更通俗易懂，从而让更多初学者更好更快的理解，是我现在继续更新博客的唯一动力了。

此外，为照顾一些传统汽车人甚至之前没听说过智能网联、自动驾驶的朋友也能从本文有所收获，故我会从智能网联、无人驾驶开始讲起，直到讲透卡尔曼滤波算法，最后到卡尔曼滤波的相关扩展算法，且过程中得到了盛、晓、叶等相关七月讲师的校正，也欢迎读者批评指正，thanks。

第一部分智能网联与无人驾驶

1.1 什么是自动驾驶/无人驾驶

一般而言，智能网联包含了自动驾驶和车联网，高级别的自动驾驶又称无人驾驶。

现在是个车企都在往自动驾驶方面投入（动辄就是上百亿），到了好像没有自动驾驶，就不是一辆可以上得了台面的车，毕竟智能三电（电池、电机、电控）、智能座舱、自动驾驶已代表未来汽车的发展趋势，所谓没自动驾驶没未来。而自动驾驶的门槛相对高，技术种类也不少，所以市面上类似的书、课程都不多（比如有一本《第一本无人驾驶技术书》，七月在线也曾于2019年推出过一个《无人驾驶实战》，后面则陆续推出过目标检测、目标跟踪、slam、感知融合等等小课）。

而无人驾驶的软件系统一般会被定义为六大模块（当然，有的模块会在不同的场景中合并）

高精度地图（即high dimensional map，此处的高精度地图不同于咱们日常生活中的那种导航地图，而是有着更高维度的信息），地图是感知、定位、预测、规划的基础
定位，包括且不限于卫星导航（比如美国GPS、俄罗斯“格洛纳斯”、欧洲“伽利略”、中国“北斗”）、惯导（IMU）、轮速计、视觉和激光雷达定位（比如激光雷达会根据激光照射到墙壁后反射回来的时间，来判断自己和墙壁之间的距离，从而判断出自己所处的位置、实现定位）
感知，估计周围物体的状态（比如位置、速度、朝向等），一般分为两个阶段：目标检测（常用手段包括各种深度学习方法，比如图像2d、图像3d、激光雷达3d、毫米波点云），和目标跟踪（常用手段包括贝叶斯滤波/卡尔曼滤波，以及深度学习相关方法，例如行人重识别person reid），且后者跟踪基于前者的检测结果
行为预测，预测周围行人和车辆的未来轨迹（位置、速度）
决策规划，包括如何自主避障、如何达到目的地的路径规划（比如A*，Dijkstra等算法）
控制，通过控制执行机构（油门、刹车、方向盘）来完成规划的加速、减速、转弯等操作

在无人驾驶里有存在四大状态的估计问题：1) 定位，估计自身状态；2）跟踪，估计周围物体状态（比如随时间变化的位置速度等）；3）建图，估计周围静态环境状态；4）标定，估计传感器之间的时空关系。而下文将提到的SLAM（同时定位与构图技术）便是解决同时定位与建图的问题。

更具体的，之前七月在线《无人驾驶实战》的授课老师盛老师有写过一篇关于自动驾驶L4级技术的短文，现引用部分内容如下：

无人驾驶要解决4 个关键问题：我在哪？我周围有什么？接下来会发生什么？我应该怎么做？

我在哪？定位、高精地图

定位需要依靠一种称为高精地图的技术，该技术会将无人车要走的所有静态环境进行描述，包括车道线、行人斑马线、标志牌等等。这些静态信息可以提供交通信号的关键信息，也会作为定位方案的锚定物对自身的位置进行校准，比如通过摄像头看到距离左边标志牌的距离是2.5m，那么在地图中知道了标志牌的坐标也就知道了自身车辆的坐标。同时，还会依靠GPS/IMU等全局设备来定位自身位置，不过这可比我们目前智能手机里的GPS精度要求高很多，通过差分融合技术可以达到厘米级精度。

我周围有什么？视觉感知、激光雷达等
有了定位后，无人车的感知系统将通过传感器和AI算法将周围的障碍物位置、大小、状态、类别等标识出来。目前主流L4级别的传感器包括GPS/IMU、LIDAR、Camera、Radar等，后三者都是用于感知周围障碍物的主要传感器，分别在不同环境下能够有不同的优势。这些信息犹如人类驾驶员的眼睛一样看到周围动态环境物体，并将其识别出来，比如精准识别车辆后方任何物体、同时关注左右两边的车辆状态，在黑暗状态时可以通过激光雷达精准识别。

接下来会发生什么？行为预测、速度预测
无人车知道周围动态物体后，还需要能够尽可能的预测这些物体的走向，包括行为预测和速度预测。例如这辆车是要左转还是直行，那辆车会不会闯红灯等等，汇入车流时速度是多少。这些问题都将决定我们无人车后续应该怎么走，如何避免碰撞发生危险。

我应该怎么做？决策、规划、控制
最后一步就是根据上述信息综合来选择一条最适合无人车的道路，如同人类的大脑一样对车辆最终的行为负责，选择最合适的方式达到目的地。这需要考虑行车的体感、安全和快捷等因素，通过最优化算法、搜索算法、蒙特卡洛树采样等多种算法来得到未来的驾驶行为。

1.2 智能网联相关岗位

针对上文智能网联汽车的定义，可以看出涉及的技术不少，每项技术背后都对应着一个个岗位

我们来具体分析其中几个岗位，比如视觉SLAM算法工程师。

那什么是slam呢？我们知道，传统的图像处理基本上是基于二维图像，而人眼是通过两只眼睛的视差（双目立体视觉）来感知周围的三维空间。随着三维视觉传感器的飞速发展，三维视觉核心技术：SLAM（全称 Simultaneous Localization And Mapping，译为同时定位与地图构建）技术，本质是对运动主体自身和周遭环境不确定性的估计，相当于核心解决两个问题：1 因为地图是未知的，所以需要估计地图（周遭环境），2 位置也是未知的，所以需要估计位置。至于常用手段则有摄像头，也有通过各种激光雷达探测距离或获取周遭环境图像的。

视觉SLAM中的传感器即为摄像头（通过摄像头同时解决定位与地图的问题）

摄像头如果使用深度相机，可以直接获取障碍物的距离，生成点云数据
当然也有用单目、双目、鱼眼摄像机的视觉SLAM ，这些摄像头需要用其他的方法才能间接的获取周围障碍物的距离

可能有同学问了，如果从零学视觉SLAM都要求掌握哪些技术呢（当然，以下所有这些技术都可以通过这个slam课掌握好）？

常用的操作系统也是Linux，这和我们做IT后台开发或AI算法研发一样，不懂Linux寸步难行，学校没学的，都得在找工作中或公司里抽时间恶补；
编程语言：C、C++，在如今AI特别火的时代，Python可以说是数据科学领域第一语言了，通过Python入门AI确实是不错的选择，但入门之后，真想在IT、AI、汽车行业真正深入发展，只懂一门Python可能就不够了，第二门语言可以是C/C++（C++ primer、深度理解C++对象模型等经典书都不错），也可以是Java（这里也有个Java与数据结构课）
SLAM相关的数学知识，包括且不限于：线性代数基础（矩阵操作）、三维空间的刚体运动、SLAM中空间点与不同的坐标系、旋转的表达（四元数、旋转矩阵、旋转向量、欧拉角）、李群与李代数、相机成像及常用视觉传感器、最小二乘法
SLAM核心技术点：视觉里程计、多视角几何、视觉里程计中的位姿估计方法、非线性优化（比如卡尔曼滤波）、回环检测与重建常用的vSLAM算法，如ORB-SLAM、SVO、DSO、MonoSLAM，VINS以及RGB-D相机等
卡尔曼滤波算法的相关算法，比如扩展卡尔曼滤波、无迹卡尔曼滤波、误差状态卡尔曼滤波器，英文简写分别为EKF、UKF、ESKF等
ROS机器人操作系统；

对于以上六点，有两点值得再提的是：比如针对第3点，不要忌惮数学，因为凡是涉及到数据相关的技术，最后都是算法，最深入都是数学（可能你此刻还不这么觉得，但当你看完全文后你一定会深以为然）；针对第4点，下面是“RGB-D相机中的直接法运用”的示意图

再比如视觉感知算法工程师，会涉及

感知算法研发和系统实现，基于视觉的障碍物检测、跟踪、行为预测等；
感知的视觉几何计算三维重建，目标检测跟踪、图像分割、图像识别等算法研发；

最后，再比如传感器融合算法高级工程师，这个岗位的岗位职责一般是：通过融合摄像头、激光雷达、毫米波雷达等传感器的感知信息，实现对周围动静环境的精确描述及预测，具体包括

多传感器多目标跟踪与意图预测，涉及感知信息的预处理、目标创建、关联、状态估计、合并与删除等等；
构建高性能的3D感知融合系统;
设计开发基于毫米波雷达稀疏点云的目标检测;
栅格地图\静态环境实时构建。

反应到岗位要求，一般有以下几点

扎实的编程能力，熟悉在Linux环境下进行C++\Python开发，理解常用数据结构及STL使用；
深入理解卡尔曼滤波等贝叶斯滤波算法，能够熟练地进行数学建模及其状态估计，深入理解常用的数据关联算法与距离计算方法；
熟悉摄像头、激光雷达、毫米波雷达等传感器，熟悉计算机视觉及其应用，有SLAM\Deep Learning基础更佳；

可见，卡尔曼滤波在感知融合里应用很广，可以对各种传感器获取到的数据进行进一步的综合处理，达到更佳的估计状态。

第二部分卡尔曼滤波算法

2.1 什么是卡尔曼滤波

关于什么是卡尔曼滤波，下面是维基百科上的解释（当然，为了通俗起见，我修改了部分描述）

卡尔曼滤波（Kalman filter）是一种高效率的递归滤波器（自回归滤波器），它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态。卡尔曼滤波会根据各测量量在不同时间下的值，考虑各时间下的联合分布，再产生对未知变数的估计，因此会比只以单一测量量为基础的估计方式要准。卡尔曼滤波得名自主要贡献者之一的鲁道夫·卡尔曼。

卡尔曼滤波的算法程序有两个步骤，分别是估计、更新：

在估计步骤中，卡尔曼滤波会产生有关目前状态的估计，其中也包括不确定性；

在更新步骤中，只要观察到下一个量测（其中一定含有某种程度的误差，包括随机噪声），会通过加权平均来修正估计值，而确定性越高的量测加权比重也越高。

算法是迭代的，可以在实时控制系统中执行，只需要目前的输入量测、以往的计算值以及其不确定性矩阵，不需要其他以往的资讯。

卡尔曼滤波之后，后续发展了一些扩展或是广义的卡尔曼滤波，例如运作在非线性系统的扩展卡尔曼滤波及无迹卡尔曼滤波（Unscented Kalman filter）。底层的模型类似隐马尔可夫模型，不过潜在变量的状态空间是连续的，而且所有潜在变量及可观测变数都是正态分布。

恩，Wikipedia上的定义向来准确严谨，唯一问题就是不够通俗、不够易懂，怎么理解更好懂呢？很简单，抽丝剥茧，一个算法相对复杂，一般来讲是因为涉及的背景知识比较多，那咱们就来一一剖析，切开了揉碎了自然就好懂了。

首先，回顾一下正太分布（又称高斯分布，一个意思）的定义

至于数学期望和方差则分别如下图所示

其次，通过一个例子理解下卡尔曼滤波的思想。

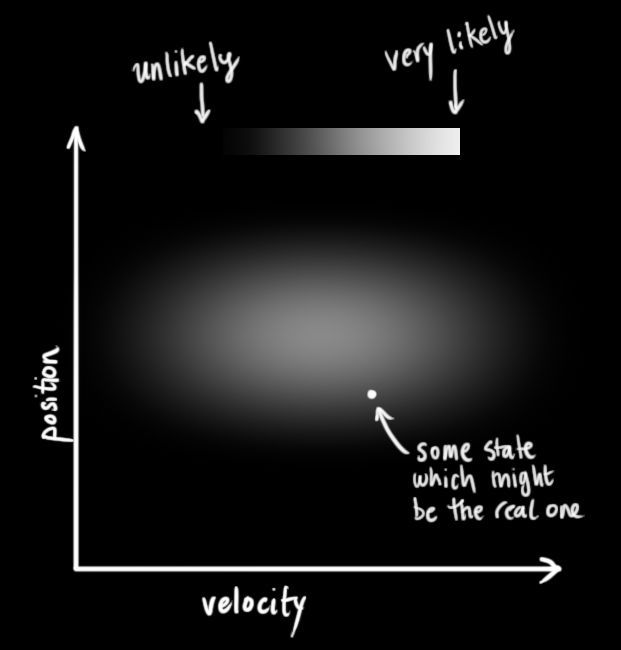
1 假设你现在有一辆车，并且已知小车在初始状态的位置如下图所示（小车的位置服从正态分布，比如可能位于正态分布的均值附近），横坐标为小车前进坐标。

有人会问，为什么是正态分布而不是确定点呢？因为在这里我们给出的是它此刻的状态估计量，对于地图上的物体，我们无法确切得出其具体的位置信息，即便你使用GPS来定位也始终会有一定的误差。因此你只能通过系统的输入（如小车的速度）和系统的输出（GPS给定的位置信息）来估算它当前的状态（真实的位置信息）。

2 然后，根据初始时刻小车的位置，我们可以预测出它在下一个时间步长的可能的位置分布。下图中可以看出，它的正态分布函数明显比上一时刻来的更宽一些。这是因为在小车运动过程中会不可避免地遇到一些随机因素的干扰，如坑洼、风、轮子打滑等，因此我们估算的位置值的不确定性变大，小车实际经过的距离与模型预测的距离不同。

3 到此刻为止，上述过程均是由我们的数学模型推算估计出来的结果，但实际上，相同的数据也可以通过传感器测量来获取，而测量值往往也呈正态分布（总之，频率派里未知值是一个确定的值，在贝叶斯派里，未知值都是一个概率分布，此点不用皱眉，很快你会有更深刻的认知），并且与我们的模型预测值有所不同，如下图中红色正态分布曲线所示，方差表示噪声测量中的不确定性。

4 这个时候咋办呢？可能你会脱口而出：将数学模型的预测值与传感器的测量值相互结合起来来获得小车的最佳位置估计值，怎么结合呢？加权平均再迭代！具体到这个例子中，咱们把这两者的概率密度函数相乘得出了当前时刻的最佳状态估计值，如图中灰色正态分布曲线所示，这就是卡尔曼滤波的核心思想，因此卡尔曼滤波也经常被称作传感器融合算法。

再然后，我们把前面的时间信息换一下，比如我们知道了上一时刻即k-1时刻小车的位置估算值，并且通过数学模型预测得到了k时刻的位置估算值，然后将其与小车传感器的测量值进行结合，得到了当前k时刻小车的最佳位置估算值。

那么问题来了，这里我们并没有给出初始状态，因此k-1时刻的位置估算值又是怎么来的呢？没错，我们是通过k-2时刻的状态量估算得来了。

2.2 卡尔曼滤波的完整流程与数学推导

通过上一节的例子，我们知晓了卡尔曼滤波的核心思想，接下来我们通过另一个例子来讨论其完整流程与数学建模推导下的细节、原理。

2.2.1 针对机器人的位置和速度建模

假如你开发了一款小型机器人，它可以在树林里自主移动。

我们可以通过一组状态变量 $\bar{x}$ 来描述机器人的状态，包括位置和速度：

$\overrightarrow{x_{k}}=(\vec{p}, \vec{v})$

下面，我们需要机器人需要明确自己的位置以便进行导航。怎么确定位置呢？

首先，我们给机器人安了一个GPS传感器，但精度只在10m。考虑到对于在机器人所处的树林里有很多溪谷和断崖，如果机器人对位置误判了哪怕只是几步远的距离，它都有可能掉到坑里，所以仅靠这个精度的GPS来定位是不够的。

我们得有更多的办法确定位置。比如我们可以获取到一些机器人的运动的信息：驱动轮子的电机指令。如果没有外界干扰，仅仅是朝一个方向前进，那么下一个时刻的位置只是比上一个时刻的位置在该方向上移动了一个固定距离。但如果有外界干扰呢？比如逆风行驶，轮子打滑，滚落颠簸地形……所以轮子转过的距离并不能完全表示机器人移动的距离，这就导致通过轮子转动预测机器人的位置不会非常准确。

如此，相当于

GPS传感器会告知我们一些关于机器人状态的信息，但是GPS可能不准；
另外，通过轮子转动可以预知机器人运动的距离，可同样也有一定的不准确度（受外力干扰）。

行到水穷处换个思路：如果我们综合“GPS + 轮子转动预测”两者的信息呢？是否可以得到比只依靠单独一个信息来源更精确的结果？显然，这就是卡尔曼滤波要解决的问题。

强调一下，前言中所说的这篇文章《How a Kalman filter works, in pictures》，形象的阐述了卡尔曼滤波的算法流程，我看过几遍，觉得还可以把卡尔曼滤波解释的更通俗些，所以我在原文图片和公式的基础上加了很多原文没有且网上其他文章也没有的大量解释、说明，以提高文章的可读性。

针对上边的系统，我们建立包括位置和速度的系统状态：

我们不知道位置和速度的准确值，但是我们可以列出一个准确数值可能落在的区间范围。在这个区间范围里，一些数值组合的可能性要高于另一些组合的可能性。

卡尔曼滤波假设所有的变量（在我们的例子中为位置和速度）是随机的且符合正态分布。每个变量有一个均值ｕ代表了随机分布的中心值（代表这是可能性最大的值），和一个方差 $\sigma^{2}$ ，用于衡量不确定度。

在上图中，位置和速度是不相关的，这意味着我们不能从一个变量推测另一个变量。

实际上呢，位置和速度是相关的。比如已知上一个状态的位置值，现在要预测下一个状态的位置值：

如果机器人的速度很快，一定的时间内，机器人可能移动得很远；
相反，如果速度很慢，同样的时间内，机器人会移动的很近。

这种关系在跟踪系统状态时很重要，因为它给了我们更多的信息：一个测量值告诉我们另一个测量值可能是什么样子。

为了捕获这种相关性，我们可以使用协方差矩阵。简而言之，矩阵中的每个元素 $\Sigma_{i j}$ 表示了第个变量和第个变量之间的关系（协方差矩阵是对称的，即交换下标和并无任何影响）。

协方差矩阵通常表示为Σ，它的元素则表示为 $\Sigma_{i j}$ ，从而有

$\Sigma_{i j}=\operatorname{Cov}\left(x_{i}, x_{j}\right)=E\left[\left(x_{i}-\mu_{i}\right)\left(x_{j}-\mu_{j}\right)\right]$

2.2.2 利用矩阵进一步描述系统状态

为了把以上关于状态的信息建模为正态分布，所以在k时刻我们需要两个信息：最佳预估值 $\bar{x}_{k}$ （均值，也就是u），和它的协方差矩阵 $P_{k}$

(这里我们只记录了位置和速度，但只要和问题相关，我们可以把任何数据变量放进系统状态里)

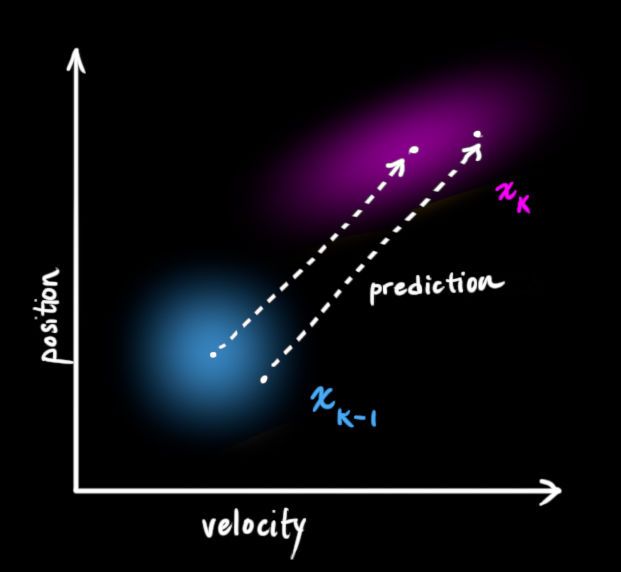
接下来，我们要通过k-1时的状态来预测下一个状态（k时）。但我们不知道状态的准确值，怎么办呢？预测函数会对k-1时刻所有可能值的范围进行预测，然后得出一个k时刻新值的分布范围。

我们可以通过一个状态转移矩阵 $F_{k}$ 来表示这个预测过程， $F_{k}$ 把k-1时刻所有可能的状态值转移到一个新的范围内（它从原始预测中取每一点，并将其移动到新的预测位置），这个新的范围代表了系统新的状态值可能存在的范围，如果k-1时刻估计值的范围是准确的话。

考虑到匀速状态下，S（路程）=v（速度）x t（时间），我们通过下述公式来描述这个"预测下个状态"的过程（别忘了， $\overrightarrow{x_{k}}=(\vec{p}, \vec{v})$ ）：

进而整理为矩阵则是：

我们现在有了一个预测矩阵，可以简单预测下个状态，但怎么更新协方差矩阵呢？

试想，如果我们对每个点进行矩阵A转换，它的协方差矩阵Σ会发生什么变化，比如

结合（4）和（3）：

2.2.3 不确定外部因素的估计：贝叶斯理论

到目前为止，我们还没有考虑到所有的影响因素，因为系统状态的改变并不只依赖上一个系统状态，外界作用力也可能会影响系统状态的变化。外界作用力分两种

第一种是人为指令，例如，在我们跟踪一列火车的运动状态时，火车驾驶员可能踩了油门使火车提速。
第二种是不受人为控制，比如2.1节提到的坑洼、风、轮子打滑等等，其所带来的变化是未知且不好预测的，没法严格确定到某个具体的值。恩，有没有熟悉的贝叶斯理论的味道了？

对于贝叶斯的理论有必要提一下（特引用我之前写的一篇贝叶斯笔记，详见参考文献5）

先看两个例子

比如有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率θ是多少？”

频率派的人会想都不用想而立马告诉你，取出白球的概率 $\theta$ 就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X 的变化而变化。

贝叶斯的理论则认为取得白球的概率是个不确定的值，因为其中含有机遇的成分。

再比如，一个朋友创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？你如果对他为人比较了解，而且有方法、思路清晰、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%~90%这个区间范围。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯式的思考方式。

换言之

频率派把需要推断的参数θ看做是固定的未知常数，即概率虽然是未知的，但最起码是确定的一个值，同时，样本X 是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X 的分布；

而贝叶斯派的观点则截然相反，他们认为参数是随机变量，而样本X 是固定的，由于样本是固定的，所以他们重点研究的是参数的分布。

针对第一种外力，在我们机器人例子中，导航软件可能发出一些指令启动或者制动轮子。这个好解决，通过一个向量 $\bar{u}_{k}$ 来描述这些信息，把它添加到我们的预测方程里作为一个修正。

假如我们通过发出的指令得到预期的加速度a，根据速度-加速度公式 $V_{t} = V_{0} + at$ ，以及加速度-位移公式 $S = v_0t + \frac{1}{2} at^{2}$ ，上边的运动方程可以变化为：

再次整理为矩阵则是：

$B_{k}$ 称作控制矩阵， $\bar{u}_{k}$ 称作控制向量（当没有任何外界动力影响的系统时，则可以忽略该项）。

针对第二种外力，则相对麻烦些了，比如受到风力影响或轮子打滑、地面上的坑坑洼洼、突起异物都使得我们跟踪的物体的速度发生不可控的变化。

怎么办呢？可以把“世界”中的这些不确定性统一建模，在预测步骤中增加一个不确定项。

相当于原始状态中的每一个点可以都预测转换到一个范围，而不是某个确定的点。转换为数学表达是： $\bar{x}_{k-1}$ 中的每个点移动到一个符合协方差 $Q_{k}$ 的高斯分布里（也就是蓝色的高斯分布移动到紫色高斯分布的位置），或者说，把这些不确定的外部因素描述为协方差为 $Q_{k}$ 的高斯噪声，具体根据预测的传感器噪声来定（比如imu或者轮速计）：

这个紫色的高斯分布拥有和原蓝色的高斯分布相同的均值，但协方差不同。

对 $Q_{k}$ 简单叠加，可以拿到扩展的协方差，这样就得到了预测步骤的完整表达式：

解释下上面（7）中的那两个式子

新的最佳估计是在原最佳估计的基础上，通过已知的外部影响校正得到的预测值。
新的不确定性则综合了原不确定性和不确定的外部因素的影响得到的预测。

到这里，我们得到了一个模糊的估计范围，一个通过 $x_{k}$ 和 $P_{k}$ 描述的范围。如果再结合我们传感器的数据呢？

2.2.4 数学模型之外再通过测量值修正预测值

实际生活当中，我们经常会用到不止一种手段来多方论证我们的预测结果，上节我们通过建立数学模型预测，此外，我们可能还有一些传感器来测量系统的状态。

当然，我们可能有好几个传感器，比如一个测量位置一个测量速度，每个传感器可以提供一些关于系统状态的数据信息（每个传感器检测一个系统变量并且产生一些读数）。

考虑到传感器测量的范围和单位可能与我们跟踪系统变量所使用的范围和单位不一致，所以需要对传感器做下建模：通过矩阵 $H_{k}$ 。

初学者刚看到这的时候可能会有疑问，这个 $H_{k}$ 到底是干啥用的？

通过上文2.1节，我们已经知晓，卡尔曼滤波实质就是将预测状态量的高斯分布和观测量的高斯分布做融合，生成一个新的高斯分布。

而很快你会通过下文发现，这个新的高斯分布的均值和方差是两个独立的高斯分布的相关参量的加权，这个加权就是卡尔曼增益，但是预测状态量和观测量可能维度不同，需要将他们同时转换到一个向量空间中，所以观测量有了线性变换矩阵 $H_{k}$ ，相当于状态域通过 $H_{k}$ 转换到观测域。

为避免降低本文的可读性，再举个例子，比如车速可以映射到轮速计的转速，车速到转速的转换关系就可以通过 $H_{k}$ 表达。

把得到的传感器读数的分布范围转换为一般形式：

换言之，我们的传感器也是有自己的精度范围的，对于一个真实的位置和速度，传感器的读数受到高斯噪声的影响会在某个范围内波动。

我们观测到的每个数据，可以认为其对应某个真实的状态。但是因为存在不确定性，某些状态的可能性比另外一些的可能性更高。

我们将这种测量值与真实值之间的不确定性（即观测传感器噪声）的协方差设为 $R_{k}$ ，均值设为 $\bar{z}_{k}$ ，具体根据观测传感器的噪声来定（比如相机、lidar）。

所以现在我们有了两个数据，一个来自于我们通过数学模型的预测值，另一个来自传感器的测量值。

我们必须尝试去把两者的数据预测值（粉色）与测量值（绿色）融合起来。

实际上对于任何状态，都有两个可能性：

传感器读数更接近系统真实状态
预测值更接近系统真实状态

怎么融合呢？概率论里，两个事件如果同时发展则相乘，所以我们尝试将两个高斯块（Gaussian blob）相乘试下：

相乘之后得到的即为重叠部分，这个区域同时属于两个高斯块，并且比单独任何一个区域都要精确。这个区域的平均值取决于我们更取信于哪个数据来源，这样通过我们手中的数据得到了一个最好的估计值。

恩，又是另一个高斯块。

事实证明，当你把两个高斯分布相乘时（各自的均值和协方差矩阵相乘），你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了：新高斯分布的均值和方差均可以通过老的均值方差求得！

2.2.5 融合两个高斯斑：卡尔曼增益出场

首先，针对一维数据开始，一维高斯（均值u，方差 $\sigma^{2}$ ）的方程被定义为：

如果两个高斯分布相乘会发生什么呢（如之前所说，预测值是粉红色，测量值是绿色），下图的蓝色曲线代表了两个高斯分布的交集部分：

把（9）带入（10）然后做一些变换，可以得到

且慢，上述公式11的推导如果不一步步展开，则会导致初学的你在千篇一律的人云亦云中看的还是很头疼，所以我们把上面的变换展开下：

$N(x,u_{0},\sigma_{0}) \cdot N(x,u_{1},\sigma_{1}) \\ = \frac{1}{\sigma_{0} \sqrt{2 \pi}} e^{-\frac{(x-\mu_{0})^{2}}{2 \sigma_{0}^{2}}} \cdot \frac{1}{\sigma_{1} \sqrt{2 \pi}} e^{-\frac{(x-\mu_{1})^{2}}{2 \sigma_{1}^{2}}} \\ = \frac{1}{\sqrt{2 \pi}}\frac{1}{\sigma_{0}\sigma_{1} \sqrt{2 \pi}} e -\frac{\sigma_{1}^{2}\left(x-u_{0}\right)^{2}+\sigma_{0}^{2}\left(x-u_{1}\right)^{2}}{2\left(\sigma_{0} \sigma_{1}\right)^{2}} \\ = \frac{1}{\sqrt{2 \pi}}\frac{1}{\sigma_{0}\sigma_{1} \sqrt{2 \pi}} e- \frac{( \sigma_{0}^{2} + \sigma_{1}^{2})x^2 - 2\left(u_{0}\sigma_{1}^{2}+u_{1} \sigma_{0}^2\right)x + \sigma_{1}^2u_{0}^2 + \sigma_{0}^2u_{1}^2 } { 2(\sigma_{0}\sigma_{1})^2} \\ = \frac{1}{\sqrt{2 \pi}}\frac{1}{\sigma_{0}\sigma_{1} \sqrt{2 \pi}} e- \frac{x^{2}-2\left(\frac{u_{0} \sigma_{1}^{2}+u_{1} \sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}\right) x+\frac{\sigma_{1}^{2} u_{0}^{2}+\sigma_{0}^{2} u_{1}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}}{2 \frac{\left(\sigma_{0} \sigma_{1}\right)^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}}$

$=A \cdot \frac{1}{\frac{\sigma_{0} \sigma_{1}} {\sqrt{\sigma_{0}^{2}+\sigma_{1}^{2}}} \sqrt{2 \pi}} e^ {- \frac {\left(x-\frac{u_{0} \sigma_{1}^{2}+u_{1} \sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}\right)^{2}} {2\left (\frac{\sigma_{0} \sigma_{1}} {\sqrt{\sigma_{0}^{2}+\sigma_{1}^2}}\right)^{2}}}$

其中，A代表其它项，从而有

$u^{\prime}=\frac{u_{0} \sigma_{1}^{2}+u_{1} \sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}=u_{0}+\frac{\left(u_{1}-u_{0}\right) \sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}$

$\sigma^{\prime}=\frac{\sigma_{0}^{2} \sigma_{1}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}=\sigma_{0}^{2}-\frac{\sigma_{0}^{4}}{\sigma_{0}^{2}+\sigma_{1}^{2}}$

因式分解出一个部分，这部分用k表示：

相当于如果是一维数据下，对于之前的预测值，仅仅是简单将两者叠加相乘就可以得到新的预测值。

如果是一个多维矩阵呢？我们将（12）与（13）表示为矩阵形式。Σ表示协方差矩阵， $\bar{u}$ 表示平均向量：

上述的这个矩阵K 就是卡尔曼增益。

现在，我们有两个独立的维度去估计系统状态：

预测值

测量值

将两者相乘带入（15）寻找他们的重叠区域：

从（14）可知，卡尔曼增益为

到了关键步骤！原文是一句带过，但为本文的通俗考虑，我多解释两句：

将（16）的第一个公式的两边都除以 $H_{k}$ 可得到（18）的第一个公式（注意，其中定义了 $K' = K/H_{k}$ ，所以结合了 $K = K' H_{k}$ ），同时（16）的第二个公式的左右两边都约掉 $H_{K} H_{K}^{T}$ ，可以得到（18）的第二个公式（一样结合了这个定义 $K = K' H_{k}$ ）

然后对（17）的两边也都同时除以 $H_{k}$ （结合了上面的定义 $K' = K/H_{k}$ ），可以得到（19）

以为就这样了？我对正在读此文的你提一个问题，上面为何要从（16）（17）除以 $H_{k}$ 变到（18）（19）呢，这就要谈到卡尔曼增益的本质了。卡尔曼增益的本质其实就是把（11）里面经常用到的一个中间结果定义了一个变量，它的物理意义在于：

根据两方面的方差来决定最终的权重，这个相信大家都已理解了；

把观测域变回到状态域：即（16）是在观测域，除以 $H_{k}$ 就可以变回到状态域（18）。可能立马就有同学疑问了，啥，为啥？这个时候别忘了之前 $H_{k}$ 的定义：状态域通过乘以 $H_{k}$ 转换到观测域，反过来观测域除以 $H_{k}$ 则变回到状态域。

2.2.6 全流程回顾：从预测传感器噪声 $Q_{k}$ 到观测传感器噪声 $R_{k}$

至此，原外文针对卡尔曼滤波的过程差不多了，但为考虑增加本文的可读性，所以我再总结如下：

回顾下整个过程

最开头，我们分别建立了系统的协方差矩阵 $P_{k}$ ，以及状态转移/预测矩阵 $F_{k}$ ，预测传感器不确定的外部因素描述为协方差为 $Q_{k}$ 的高斯噪声；

随后把预测状态量到观测量的变换矩阵设为 $H_{k}$ ，测量值与真实值之间的不确定性（即观测传感器噪声）的协方差设为 $R_{k}$ ，读数的平均值为 $\bar{z}_{k}$

进而求出了卡尔曼增益的计算公式：

$K' =\frac{P_{k}H_{k}^{T} }{H_{k} P_{k} H_{k}^{T}+R_{k}}$

再回到递推公式（核心思想就是用测量值修正预测值）

$\hat{\mathbf{x}}_{k}^{\prime}=\hat{\mathbf{x}}_{k}+\mathbf{K}^{\prime}\left(\overrightarrow{\mathbf{z}_{k}}-\mathbf{H}_{k} \hat{\mathbf{x}}_{k}\right)$

从而有

特别大的时候（测量值相对不靠谱，毕竟R代表传感器噪声，R越大代表噪声越大，也就意味着测量值越不靠谱），卡尔曼增益趋于零，也就是去更多相信预测值 $\hat{x}_{k}$ ；

当特别小的时候（测量值相对靠谱），卡尔曼增益就是 $K' =H_{k}^{-1}$ ，从而代入递推公式，可得 $\hat{\mathbf{x}}_{k}^{\prime}=\hat{\mathbf{x}}_{k}+\mathbf{K}^{\prime}\left(\overrightarrow{\mathbf{z}_{k}}-\mathbf{H}_{k} \hat{\mathbf{x}}_{k}\right) = K' \overrightarrow{\mathbf{z_{k}}}$

也算是再次验证了卡尔曼滤波里的数据融合思想。

终于，我们得到了最佳预测值 $\tilde{x}_{k}^{\prime}$ ，可以把它继续放进去做另一轮预测，持续迭代（独立于 $P_{k}^{\prime}$ ）。

以上所有公式，仅需要实现（7）（18）（19），这使你可以对任何线性系统建模。

公式7类似于预测未来，公式18、19类似修正当下，简言之，则是前者预测后者更新。

另外，有一点值得一提的是，公式18中括号里的部分就是所谓的“更新量”，这个更新量的物理意义是实际与期望测量值的误差，而卡尔曼增益则是这部分更新量对于预测值的权重。

当然，卡尔曼滤波的推导思路很多：1 从加权的角度；2 从贝叶斯的角度；3 从最小二乘角度。限于篇幅，本文只介绍加权的角度，至于后两者，读者可以自行查阅相关文章，比如参考文献14的《机器人学中的状态估计》，这本书讲得不错，可能相关符号的表示有所差别（比如本文里的、 $\mathbf{B}_{k} \overrightarrow{\mathbf{u}_{k}}$ 、 $H_{k}$ 、 $\bar{z}_{k}$ 在书中分别是、 $v_{k}$ 、 $C_{k}$ 、 $y_{k}$ ），但不影响理解，拍图如下，最后还可以看下参考文献18、19。

至于非线性系统，则可以使用扩展卡尔曼滤波（Extended Kalman Filter，EKF），相当于对测量和预测值的平均值进行简单线性化，下部分会详细介绍。

第三部分卡尔曼滤波的相关扩展算法

3.1 扩展卡尔曼滤波EKF

3.1.1 什么是EKF：KF的非线性扩展

还记得前言中说的这句话不：“这算法神到什么程度呢，比如有人号称当年阿波罗就靠它登陆上的月球 :) ” ，哈哈，实际上，此言不虚。

当年登月的美国宇航工程师就曾把卡尔曼滤波用于阿波罗计划非常的轨迹估计问题中，进而导出了后面发展而来的扩展卡尔曼滤波器，具体工作包括

将KF扩展到非线性的运动、观测模型；
提出了减小非线性影响的线性化方法；
将原始的KF重新公式化为目前熟知的标准形式（预测+更新）

换言之

当系统为线性高斯模型（正太分布）时，卡尔曼滤波器能给出最优的估计，但是实际系统总是存在不同程度的非线性，如平方、三角关系、开方等。相当于系统的状态转移函数（对应状态转移矩阵），和观测函数（对应观测变换矩阵）均为非线性函数。
对于非线性系统，可以采用的一种方法是通过线性化方法将非线性系统转换为近似的线性系统，即为扩展卡尔曼滤波EKF，核心思想是：围绕滤波值将非线性函数展开成泰勒级数并略去二阶及以上项，得到一个近似的线性化模型，然后应用卡尔曼滤波完成状态估计。

3.1.2 EFK的一个示例：跟踪汽车运动轨迹

为形象说明，我们再看另外一个例子，即通过毫米波雷达跟踪汽车的运动轨迹

首先，定义如下变量（图引自Udacity）

其次，假定我们把观测值z与预测值x'之间的差值记为y，则可以有

用 $p_{x}$ 、 $p_{y}$ 以及 $v_{x}$ 、 $v_{y}$ 表示预测后的位置及速度，可得

通过一系列的换算可得（中间换算过程可以看参考文献20，本文限于篇幅则不再把中间换算过程一一列出，毕竟本部分不是本文重点，了解下思想即可）

从上面的公式很容易看出，等式两边的转化是非线性的，并不存在一个常数矩阵H，能够使得等式两边成立。

如果将高斯分布作为输入，输入到一个非线性函数中，得到的结果将不再符合高斯分布，也就将导致卡尔曼滤波的公式不再适用。

因此我们需要将上面的非线性函数转化为近似的线性函数求解。

在大学课程《高等数学》中我们学过，非线性函数y=h(x)可通过泰勒公式在点 $(x_{0},y_{0})$ 处展开为泰勒级数：

忽略二次以上的高阶项，即可得到近似的线性化方程，用以替代非线性函数h(x)，即：

将非线性函数h(x)拓展到多维，即求各个变量的偏导数，即：

对x求偏导数所对应的这一项被称为雅可比（Jacobian）式。

雅克比矩阵是函数的一阶偏导数以一定方式排列成的矩阵，通俗讲则是

一元数量函数的导数是一个数量，即斜率

多元数量函数的导数是一个向量，即梯度

多元向量值函数的导数是一个矩阵，即 Jacobia

更多请看参考文献21，从其发明历史步步深入。

我们将求偏导数的公式与之前推导的公式对应起来看x的系数，会发现这里的测量矩阵H其实就是泰勒公式中的雅可比式。

多维的雅可比式的推导过程有兴趣的同学可以自己研究一下，这里我们直接使用其结论：

求得非线性函数h(x')对 $p_{x}$ 、 $p_{y}$ 、 $v_{x}$ 、 $v_{y}$ 的一阶偏导数，并排列成的矩阵，最终得到雅克比（Jacobian）矩阵H：

其中

接下来就是考验各位高等数学求偏导数功底的时候了！

经过一系列计算，最终得到测量矩阵H为：

根据以上公式可知，在每次预测障碍物的状态后，需要根据预测的位置和速度计算出对应的测量矩阵H，这个测量矩阵为非线性函数h(x')在x'所在位置进行求导的结果。

3.2 无迹卡尔曼滤波UKF

既然EKF已经能够很好的解决非线性问题了，为什么还需要UKF？
原因是现实生活中存在很多完全不规律的分布，我们需要更好的近似方式和更高的性能。让我们来看下在EKF中如何解决非线性问题的（下图来自参考文献15，巧的是作者William还是湖南老乡 + 微信好友）：

可以看到原始高斯分布经过非线性变换之后其实是一个不规则的非线性分布，在EKF中我们在高斯均值点附近用泰勒级数近似非线性分布，从而获得近似高斯分布。但是问题在于，这个近似高斯分布有时不是足够精确，单单一个均值点往往无法预测上图中这种很不规则的分布的。这个时候我们就需要无迹卡尔曼滤波UKF了。

UKF从原始高斯分布中提取包括均值点在内的一系列代表点，并将代表点带入到非线性等式中，围绕这些点进行近似，从而获得更好的近似结果。

在上图中我们可以看到，蓝色椭圆代表的UKF近似高斯分布更接近真实的不规则分布。
总的来说，与EKF相比，UKF是处理非线性过程模型或非线性测量模型的更好的替代方法。UKF不会对非线性函数进行线性化处理，它用所谓的sigma 点来近似概率分布。其优势在于在很多情况下，sigma 点近似非线性转换的效果比线性化更好，此外它还可以省去计算复杂的雅可比矩阵的过程。更多可以查看参考文献16。

参考文献与扩展阅读

智能网联汽车技术路线图2.0及创新应用路线图
如何入门学习自动驾驶技术（一）
七月在线《无人驾驶实战》小课
Wikipedia上关于卡尔曼滤波的解释
从贝叶斯方法谈到贝叶斯网络
如何通俗理解隐马尔可夫模型HMM？
卡尔曼滤波通俗易懂的解释
关于卡尔曼滤波的经典外文：《How a Kalman filter works, in pictures》
这是上文的其中一个翻译版：如何通俗并尽可能详细地解释卡尔曼滤波？
这是上文的另外一个翻译版：图说卡尔曼滤波，一份通俗易懂的教程，这两个翻译版都有各自的一些小问题，当然，本文已避免
《概率机器人 [Probabilistic robotics]》，Google无人驾驶创始人Sebastian Thrun等人所著，本书权威且推导全面但不够通俗
《视觉SLAM十四讲：从理论到实践（第2版）》，挺不错的一本书，结合七月SLAM课足够掌握SLAM了
卡尔曼增益推导
《机器人学中的状态估计》，状态估计方向的必读书，相比《概率机器人》更通俗些，而且有意思的是，这本书的译者就是视觉SLAM十四讲的作者高翔等人
SLAM基础-扩展卡尔曼滤波
自动驾驶感知融合-无迹卡尔曼滤波(Lidar&Radar)
数据挖掘中所需的概率论与数理统计知识
贝叶斯视角下的卡尔曼滤波
从最小二乘到Kalman滤波
通俗易懂理解——卡尔曼滤波与扩展卡尔曼滤波
雅可比矩阵几何意义的直观解释及应用
卡尔曼滤波器实现详解

后记

总算成文了，坦诚讲，我在写本篇博客之前虽然看过很多文章、资料，但在动笔之前并没有对卡尔曼滤波及其相关算法有足够清晰透彻的理解，是边写边清晰的。

包括中秋三天一直在完善本文，写博十年以来，心中总有一个执念，那就是要让没有学过计算机的也能看懂我写的文章（否则何必写），所以会特别注重这两点：

多图、多举例
在他人文章中那些一步到位的推导，在我这，能拆成10步则必会拆成10步

因为只有足够通俗易懂，才可以让更多初学者更快入门，才能让我更有成就感、满足感，当然，欢迎大家不吝批评指正，最后，更深入的可以看下七月在线相关的课。

以下是本文的修改记录（开写后的一周内，基本一天一改进/深入）：

9.19，改进1.1节，特别是无人驾驶软件架构的六大模块；
9.20，改进2.1节什么是卡尔曼滤波；
9.21，改进2.2节，主要是卡尔曼增益的推导
9.22，再次改进2.2节，主要是卡尔曼增益的物理意义；
9.23，再次改进2.2节，主要总结卡尔曼滤波的三种推导思路，以及优化3.1节扩展卡尔曼滤波EKF
10.10，七月晓老师帮完善和修正1.1节的相关细节
10.11，七月晓老师帮完善预测传感器噪声协方差 $Q_{k}$ 和观测传感器噪声协方差 $R_{k}$ 的选取依据，具体来说则是 $Q_{k}$ 根据预测的传感器噪声来定（比如imu或者轮速计）， $R_{k}$ 根据观测传感器的噪声来定（比如相机、lidar）

July，二零二一年九月十七日开写，最后更新于十月十一日。

你可能感兴趣的:(AI应用：CV,NLP,推荐,算法,概率论,机器学习)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
android系统selinux中添加新属性property 辉色投像
1.定位/android/system/sepolicy/private/property_contexts声明属性开头：persist.charge声明属性类型：u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
【iOS】MVC设计模式 Magnetic_h ios mvc 设计模式 objective-c 学习 ui
MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
element实现动态路由+面包屑软件技术NINI vue案例 vue.js 前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
C语言宏函数南林yan C语言 c语言
一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
c++ 的iostream 和 c++的stdio的区别和联系黄卷青灯77 c++算法开发语言 iostream stdio
在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
LocalDateTime 转 String igotyback java 开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
swagger访问路径 igotyback swagger
Swagger2.x版本访问地址：http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口，通常为8080。{context-path}是你的应用上下文路径，如果应用部署在根路径下，则为空。Swagger3.x版本对于Swagger3.x版本（也称为OpenAPI3）访问地址：http://{ip
Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码说私域人工智能小程序
摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
每日一题——第八十九题互联网打工人no1 C语言程序设计每日一练 c语言
题目：在字符串中找到提取数字，并统计一共找到多少整数，a123xxyu23&8889，那么找到的整数为123，23，8889//思想：#include#include#includeintmain(){charstr[]="a123xxyu23&8889";intcount=0;intnum=0;//用于临时存放当前正在构建的整数。boolinNum=false;//用于标记当前是否正在读取一个整
每日一题——第八十一题互联网打工人no1 C语言程序设计每日一练 c语言
打印如下图案:#includeintmain(){inti,j;charch='A';for(i=1;i<5;i++,ch++){for(j=0;j<5-i;j++){printf("");//控制空格输出}for(j=1;j<2*i;j++)//条件j<2*i{printf("%c",ch);//控制字符输出}printf("\n");}return0;}
每日一题——第八十二题互联网打工人no1 C语言程序设计每日一练 c语言
题目：将一个控制台输入的字符串中的所有元音字母复制到另一字符串中#include#include#include#include#defineMAX_INPUT1024boolisVowel(charp);intmain(){charinput[MAX_INPUT];charoutput[MAX_INPUT];printf("请输入一串字符串：\n");fgets(input,sizeof(inp
每日一题——第八十三题互联网打工人no1 C语言程序设计每日一练 c语言
题目：将输入的整形数字输出,输出1990，输出"1990"#include#defineMAX_INPUT1024intmain(){intarrr_num[MAX_INPUT];intnum,i=0;printf("请输入一个数字：");scanf_s("%d",&num);while(num!=0){arrr_num[i++]=num%10;num/=10;}printf("\"");for(
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
腾讯云技术深度探索：构建高效云原生微服务架构我的运维人生云原生架构腾讯云运维开发技术共享
腾讯云技术深度探索：构建高效云原生微服务架构在当今快速发展的技术环境中，云原生技术已成为企业数字化转型的关键驱动力。腾讯云作为行业领先的云服务提供商，不断推出创新的产品和技术，助力企业构建高效、可扩展的云原生微服务架构。本文将深入探讨腾讯云在微服务领域的最新进展，并通过一个实际案例展示如何在腾讯云平台上构建云原生应用。腾讯云微服务架构概览腾讯云微服务架构基于云原生理念，旨在帮助企业快速实现应用的容
怎么起诉借钱不还的人？怎样起诉欠款不还的人？影子爱学习
怎么起诉借钱不还的人？怎样起诉欠款不还的人？如果遇到难以解决的法律问题，我们可以匹配专业律师。例如：婚姻家庭（离婚纠纷）、刑事辩护、合同纠纷、债权债务、房产（继承）纠纷、交通事故、劳动争议、人身损害、公司相关法律事务（法律顾问）等咨询推荐手机/微信:15633770876【全国案件皆可】借钱不还起诉对方需要哪些资料起诉欠钱不还的，一般需要的材料包括以下这些：借据、收据、欠条、付款凭证等证据，以及向
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
使用 FinalShell 进行远程连接（ssh 远程连接 Linux 服务器）编程经验分享开发工具服务器 ssh linux
目录前言基本使用教程新建远程连接连接主机自定义命令路由追踪前言后端开发，必然需要和服务器打交道，部署应用，排查问题，查看运行日志等等。一般服务器都是集中部署在机房中，也有一些直接是云服务器，总而言之，程序员不可能直接和服务器直接操作，一般都是通过ssh连接来登录服务器。刚接触远程连接时，使用的是XSHELL来远程连接服务器，连接上就能够操作远程服务器了，但是仅用XSHELL并没有上传下载文件的功能
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
2020-04-12每天三百字之连接与替代冷眼看潮
不知道是不是好为人师，有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程，就是不断连接与替代的过程。人类发现了火并应用火以后，告别了茹毛饮血的野兽般的原始生活（火烧、烹饪替代了生食）人类用石器代替了完全手工，工具的使用使人类进步一大步。类似这样的替代还有很多，随着科技的发展，有更多的原始的事物被替代，代之以更高效、更先进的技术。在近现代，汽车替代了马车，高速公路和铁路
【加密社】Solidity 中的事件机制及其应用加密社闲侃区块链智能合约区块链
加密社引言在Solidity合约开发过程中，事件（Events）是一种非常重要的机制。它们不仅能够让开发者记录智能合约的重要状态变更，还能够让外部系统（如前端应用）监听这些状态的变化。本文将详细介绍Solidity中的事件机制以及如何利用不同的手段来触发、监听和获取这些事件。事件存储的地方当我们在Solidity合约中使用emit关键字触发事件时，该事件会被记录在区块链的交易收据中。具体而言，事件
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
使用Apify加载Twitter消息以进行微调的完整指南 nseejrukjhad twitter easyui 前端 python
#使用Apify加载Twitter消息以进行微调的完整指南##引言在自然语言处理领域，微调模型以适应特定任务是提升模型性能的常见方法。本文将介绍如何使用Apify从Twitter导出聊天信息，以便进一步进行微调。##主要内容###使用Apify导出推文首先，我们需要从Twitter导出推文。Apify可以帮助我们做到这一点。通过Apify的强大功能，我们可以批量抓取和导出数据，适用于各类应用场景。
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
利用LangChain的StackExchange组件实现智能问答系统 nseejrukjhad langchain microsoft 数据库 python
利用LangChain的StackExchange组件实现智能问答系统引言在当今的软件开发世界中，StackOverflow已经成为程序员解决问题的首选平台之一。而LangChain作为一个强大的AI应用开发框架，提供了StackExchange组件，使我们能够轻松地将StackOverflow的海量知识库集成到我们的应用中。本文将详细介绍如何使用LangChain的StackExchange组件
开发者关心的那些事圣子足道 ios 游戏编程 apple 支付
我要在app里添加IAP，必须要注册自己的产品标识符（product identifiers）。产品标识符是什么？产品标识符（Product Identifiers）是一串字符串，它用来识别你在应用内贩卖的每件商品。App Store用产品标识符来检索产品信息，标识符只能包含大小写字母（A-Z）、数字（0-9）、下划线（-）、以及圆点(.)。你可以任意排列这些元素，但我们建议你创建标识符时使用
负载均衡器技术Nginx和F5的优缺点对比 bijian1013 nginx F5
对于数据流量过大的网络中，往往单一设备无法承担，需要多台设备进行数据分流，而负载均衡器就是用来将数据分流到多台设备的一个转发器。目前有许多不同的负载均衡技术用以满足不同的应用需求，如软/硬件负载均衡、本地/全局负载均衡、更高
LeetCode[Math] - #9 Palindrome Number Cwind java Algorithm 题解 LeetCode Math
原题链接：#9 Palindrome Number 要求：判断一个整数是否是回文数，不要使用额外的存储空间难度：简单分析：题目限制不允许使用额外的存储空间应指不允许使用O(n)的内存空间，O(1)的内存用于存储中间结果是可以接受的。于是考虑将该整型数反转，然后与原数字进行比较。注：没有看到有关负数是否可以是回文数的明确结论，例如
画图板的基本实现 15700786134 画图板
要实现画图板的基本功能，除了在qq登陆界面中用到的组件和方法外，还需要添加鼠标监听器，和接口实现。首先，需要显示一个JFrame界面： public class DrameFrame extends JFrame { //显示
linux的ps命令被触发 linux
Linux中的ps命令是Process Status的缩写。ps命令用来列出系统中当前运行的那些进程。ps命令列出的是当前那些进程的快照，就是执行ps命令的那个时刻的那些进程，如果想要动态的显示进程信息，就可以使用top命令。要对进程进行监测和控制，首先必须要了解当前进程的情况，也就是需要查看当前进程，而 ps 命令就是最基本同时也是非常强大的进程查看命令。使用该命令可以确定有哪些进程正在运行
Android 音乐播放器下一曲连续跳几首歌肆无忌惮_ android
最近在写安卓音乐播放器的时候遇到个问题。在MediaPlayer播放结束时会回调 player.setOnCompletionListener(new OnCompletionListener() { @Override public void onCompletion(MediaPlayer mp) { mp.reset(); Log.i("H
java导出txt文件的例子知了ing java servlet
代码很简单就一个servlet,如下： package com.eastcom.servlet; import java.io.BufferedOutputStream; import java.io.IOException; import java.net.URLEncoder; import java.sql.Connection; import java.sql.Resu
Scala stack试玩, 提高第三方依赖下载速度矮蛋蛋 scala sbt
原文地址： http://segmentfault.com/a/1190000002894524 sbt下载速度实在是惨不忍睹, 需要做些配置优化下载typesafe离线包, 保存为ivy本地库 wget http://downloads.typesafe.com/typesafe-activator/1.3.4/typesafe-activator-1.3.4.zip 解压r
phantomjs安装(linux，附带环境变量设置) ，以及casperjs安装。 alleni123 linux spider
1. 首先从官网 http://phantomjs.org/下载phantomjs压缩包，解压缩到/root/phantomjs文件夹。 2. 安装依赖 sudo yum install fontconfig freetype libfreetype.so.6 libfontconfig.so.1 libstdc++.so.6 3. 配置环境变量 vi /etc/profil
JAVA IO FileInputStream和FileOutputStream，字节流的打包输出百合不是茶 java核心思想 JAVA IO操作字节流
在程序设计语言中，数据的保存是基本，如果某程序语言不能保存数据那么该语言是不可能存在的，JAVA是当今最流行的面向对象设计语言之一，在保存数据中也有自己独特的一面，字节流和字符流 1，字节流是由字节构成的，字符流是由字符构成的字节流和字符流都是继承的InputStream和OutPutStream ,java中两种最基本的就是字节流和字符流类 FileInputStream
Spring基础实例（依赖注入和控制反转） bijian1013 spring
前提条件：在http://www.springsource.org/download网站上下载Spring框架，并将spring.jar、log4j-1.2.15.jar、commons-logging.jar加载至工程1.武器接口 package com.bijian.spring.base3; public interface Weapon { void kil
HR看重的十大技能 bijian1013 提升能力 HR 成长
一个人掌握何种技能取决于他的兴趣、能力和聪明程度，也取决于他所能支配的资源以及制定的事业目标，拥有过硬技能的人有更多的工作机会。但是，由于经济发展前景不确定，掌握对你的事业有所帮助的技能显得尤为重要。以下是最受雇主欢迎的十种技能。　　一、解决问题的能力　　每天，我们都要在生活和工作中解决一些综合性的问题。那些能够发现问题、解决问题并迅速作出有效决
【Thrift一】Thrift编译安装 bit1129 thrift
什么是Thrift The Apache Thrift software framework, for scalable cross-language services development, combines a software stack with a code generation engine to build services that work efficiently and s
【Avro三】Hadoop MapReduce读写Avro文件 bit1129 mapreduce
Avro是Doug Cutting(此人绝对是神一般的存在）牵头开发的。开发之初就是围绕着完善Hadoop生态系统的数据处理而开展的（使用Avro作为Hadoop MapReduce需要处理数据序列化和反序列化的场景）,因此Hadoop MapReduce集成Avro也就是自然而然的事情。这个例子是一个简单的Hadoop MapReduce读取Avro格式的源文件进行计数统计，然后将计算结果
nginx定制500，502，503，504页面 ronin47 nginx　错误显示
server { listen 80; error_page 500/500.html; error_page 502/502.html; error_page 503/503.html; error_page 504/504.html; location /test {return502;}} 配置很简单，和配
java-1.二叉查找树转为双向链表 bylijinnan 二叉查找树
import java.util.ArrayList; import java.util.List; public class BSTreeToLinkedList { /* 把二元查找树转变成排序的双向链表题目：输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。要求不能创建任何新的结点，只调整指针的指向。 10 / \ 6 14 / \
Netty源码学习-HTTP-tunnel bylijinnan java netty
Netty关于HTTP tunnel的说明： http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/socket/http/package-summary.html#package_description 这个说明有点太简略了一个完整的例子在这里： https://github.com/bylijinnan
JSONUtil.serialize(map)和JSON.toJSONString(map)的区别 coder_xpf jquery json map val()
JSONUtil.serialize(map)和JSON.toJSONString(map)的区别数据库查询出来的map有一个字段为空通过System.out.println()输出 JSONUtil.serialize(map)： {"one":"1","two":"nul
Hibernate缓存总结 cuishikuan 开源 ssh javaweb hibernate缓存三大框架
一、为什么要用Hibernate缓存？ Hibernate是一个持久层框架，经常访问物理数据库。为了降低应用程序对物理数据源访问的频次，从而提高应用程序的运行性能。缓存内的数据是对物理数据源中的数据的复制，应用程序在运行时从缓存读写数据，在特定的时刻或事件会同步缓存和物理数据源的数据。二、Hibernate缓存原理是怎样的？ Hibernate缓存包括两大类：Hib
CentOs6 dalan_123 centos
首先su - 切换到root下面1、首先要先安装GCC GCC-C++ Openssl等以来模块：yum -y install make gcc gcc-c++ kernel-devel m4 ncurses-devel openssl-devel2、再安装ncurses模块yum -y install ncurses-develyum install ncurses-devel3、下载Erang
10款用 jquery 实现滚动条至页面底端自动加载数据效果 dcj3sjt126com JavaScript
无限滚动自动翻页可以说是web2.0时代的一项堪称伟大的技术，它让我们在浏览页面的时候只需要把滚动条拉到网页底部就能自动显示下一页的结果，改变了一直以来只能通过点击下一页来翻页这种常规做法。无限滚动自动翻页技术的鼻祖是微博的先驱：推特(twitter)，后来必应图片搜索、谷歌图片搜索、google reader、箱包批发网等纷纷抄袭了这一项技术，于是靠滚动浏览器滚动条
ImageButton去边框&Button或者ImageButton的背景透明 dcj3sjt126com imagebutton
在ImageButton中载入图片后，很多人会觉得有图片周围的白边会影响到美观，其实解决这个问题有两种方法一种方法是将ImageButton的背景改为所需要的图片。如：android:background="@drawable/XXX" 第二种方法就是将ImageButton背景改为透明，这个方法更常用在XML里； <ImageBut
JSP之c:foreach eksliang jsp forearch
原文出自：http://www.cnblogs.com/draem0507/archive/2012/09/24/2699745.html <c:forEach>标签用于通用数据循环，它有以下属性属性描述是否必须缺省值 items 进行循环的项目否无 begin 开始条件否 0 end 结束条件否集合中的最后一个项目 step 步长否 1
Android实现主动连接蓝牙耳机 gqdy365 android
在Android程序中可以实现自动扫描蓝牙、配对蓝牙、建立数据通道。蓝牙分不同类型，这篇文字只讨论如何与蓝牙耳机连接。大致可以分三步：一、扫描蓝牙设备： 1、注册并监听广播： BluetoothAdapter.ACTION_DISCOVERY_STARTED BluetoothDevice.ACTION_FOUND BluetoothAdapter.ACTION_DIS
android学习轨迹之四：org.json.JSONException: No value for hyz301 json
org.json.JSONException: No value for items 在JSON解析中会遇到一种错误，很常见的错误 06-21 12:19:08.714 2098-2127/com.jikexueyuan.secret I/System.out﹕ Result:{"status":1,"page":1,&
干货分享：从零开始学编程系列汇总 justjavac 编程
程序员总爱重新发明轮子，于是做了要给轮子汇总。从零开始写个编译器吧系列 (知乎专栏) 从零开始写一个简单的操作系统 (伯乐在线) 从零开始写JavaScript框架 (图灵社区) 从零开始写jQuery框架 (蓝色理想 ) 从零开始nodejs系列文章 (粉丝日志) 从零开始编写网络游戏
jquery-autocomplete 使用手册 macroli jquery Ajax 脚本
jquery-autocomplete学习一、用前必备官方网站：http://bassistance.de/jquery-plugins/jquery-plugin-autocomplete/ 当前版本：1.1 需要JQuery版本：1.2.6 二、使用 <script src="./jquery-1.3.2.js" type="text/ja
PLSQL-Developer或者Navicat等工具连接远程oracle数据库的详细配置以及数据库编码的修改超声波 oracle plsql
　　在服务器上将Oracle安装好之后接下来要做的就是通过本地机器来远程连接服务器端的oracle数据库，常用的客户端连接工具就是PLSQL-Developer或者Navicat这些工具了。刚开始也是各种报错，什么TNS:no listener;TNS:lost connection;TNS:target hosts...花了一天的时间终于让PLSQL-Developer和Navicat等这些客户
数据仓库数据模型之：极限存储--历史拉链表 superlxw1234 极限存储数据仓库数据模型拉链历史表
在数据仓库的数据模型设计过程中，经常会遇到这样的需求： 1. 数据量比较大; 2. 表中的部分字段会被update,如用户的地址，产品的描述信息，订单的状态等等; 3. 需要查看某一个时间点或者时间段的历史快照信息，比如，查看某一个订单在历史某一个时间点的状态，比如，查看某一个用户在过去某一段时间内，更新过几次等等; 4. 变化的比例和频率不是很大，比如，总共有10
10点睛Spring MVC4.1-全局异常处理 wiselyman spring mvc
10.1 全局异常处理使用@ControllerAdvice注解来实现全局异常处理; 使用@ControllerAdvice的属性缩小处理范围 10.2 演示演示控制器 package com.wisely.web; import org.springframework.stereotype.Controller; import org.spring