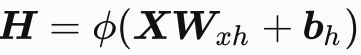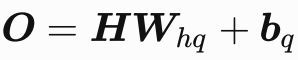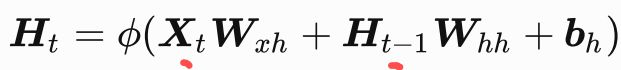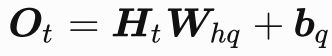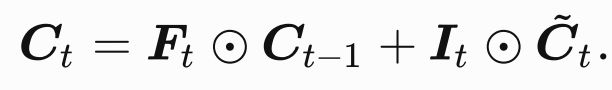Pytorch入门之RNN

看了花书上的RNN和莫凡python关于RNN的实战演练，现在来总结一下：

主要分5部分：

1、LSTM实现MNIST数据集分类

2、RNN实现三角函数的回归问题

3、LSTM实现三角函数的回归问题

4、深度循环神经网络

5、RNN实现语言模型

6、LSTM实现语言模型

 

一、RNN基本结构

在4部分的实战之前，首先需要准备RNN基础知识：

RNN，循环神经网络，是用于处理和离散时间序列有关的神经网络，相较于CNN，RNN加入了时间信息、还有记忆信息的特点。

RNN通过一种称之为隐藏状态来记忆当前时间步之前的信息，然后将它和当前时间步的输入一起结合输出下一个隐藏状态。

对于多层感知机的实现，我们起初都是用一个FC层去联合输入，然后通过非线性函数，得到一个分数，即：

 

RNN是怎样的呢？其实就是多了一个输入罢了：

这里的t是当前的时间步，t-1前一个时间点。Ht是当前时间步的隐藏变量。

可见RNN引入了一个存储了上个时间步的输出的隐藏状态变量Ht-1，以及一个新的weight权重参数。

 RNN网络的参数：

note：

1、每个时间步都是共用一套weight的。

2、这里d是当前时间步输入Xt的长度（神经元个数）；h是全连接层的神经元个数；q是输出层的神经元个数；n是batch的大小；T是时间步的总长。

3、weight、bias都来自于全连接层的参数。

 4、在pytorch实现的RNN中，Ht的size是：(batch, T, h)；Xt的size是：(batch, T, d); 输出的size：(batch, q)

 

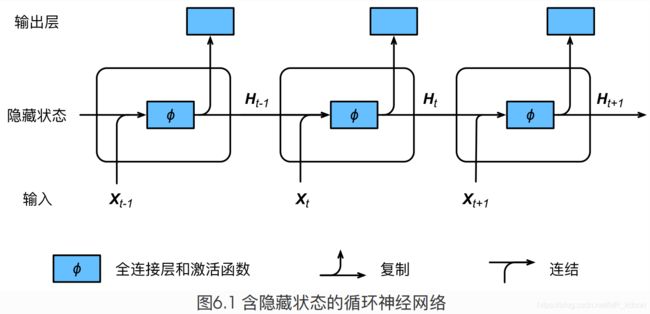
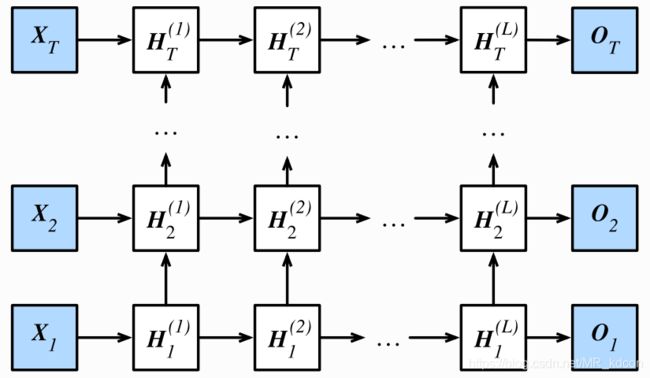
下面是3个时间步的网络inference过程，由于在当前时间点会得到上个时间段综合来的信息，而上个时间段综合来的信息又和当前输入一起得到当前时间的信息，因此是个循环的过程，这个循环的结构，可以称之为细胞（为了和LSTM统一起来），也就是下图中的每一个小矩形框，每个细胞都会有一个输出，就是复制的那部分。整个RNN网络就是由T个细胞连接而成。

                                                图1

 

 

二、RNN存在的主要问题：

反向传播时候的梯度消失或者梯度爆炸。下面我用数学分析和举例来论证。 

数学分析：

时间总步数T的损失函数：

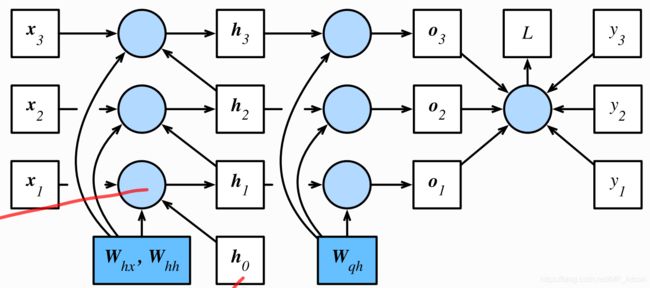
 整个网络图如下：

                                                图2 

接下来我们基于计算图来推导反向梯度传播

下面是我手画的计算图：

总结就是：

随着时间序列的加深，最初的序列容易出现梯度爆炸或梯度消失现象，使用优化算法（如SGD）之后，网络就停止了学习。接下来来用一个实际例子来说明RNN这个缺陷：

假设我们需要用RNN做一个分类问题，给一段时间序列，让他去判别输出是什么物品。

时间序列：

小刚今天买了一个篮球，花了100元，然后我抱着.......(此处省略1000字)，最后和小明一起回家了。

要求判别小刚买了什么？分类器最初肯定是乱答的，可能说是薯片。

RNN是怎么去判别呢？首先整段文字的很前面就出现了答案“篮球”，然后这个篮球信息将会随着前向传播一直传，传到最后的输出层。薯片和篮球误差很大，接着就要开始反向传播了，我们根据上面每经过一个细胞，Ht-1都需要乘以weight参数，因此Whh小于1的时候，当传到很前面的时候，误差几乎为0，且梯度消失，使得浅层的参数不更新，就无法将正确答案传到输出层，预测出正确的结果。

 

三、LSTM基本结构

为了克服这个缺陷，LSTM就登场了。

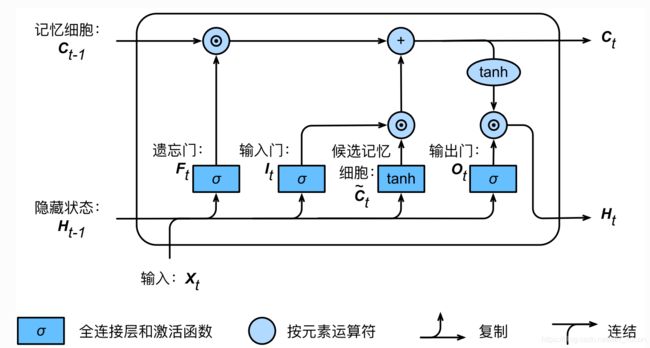
LSTM引入了3个门：即输入门、遗忘门、输出门，以及1个记忆细胞和1个候选记忆细胞。

如下图所示，多了3个门1个候选记忆细胞，就有8组weight和4组bias ，这一个矩形结构称为一个细胞,每个细胞都会有一个输出

 

 

第五个就是记忆细胞： 

 

 

 

 

四、LSTM进行MNIST数据集分类 

多对一模型

数据集导入->批量化包装->LSTM网络实现->训练->测试

4.1、前面就不说了，直接进入LSTM网络是如何编写的

class Rnnnet(nn.Module):
    def __init__(self):
        super().__init__()
        self.rnn = nn.LSTM(
            input_size=28,  # 每一步的单个样本输入大小
            hidden_size=64,  # 每个细胞中隐藏层神经元个数
            num_layers=1,  # 每个细胞中FC的层数
            # 数据格式True：(batch, time_step, imput_size) False:(time_step, batch, input_size)
            batch_first=True
        )
        self.fc = nn.Linear(64, 10)  # 用于分类，所以需要一个FC层，注意FC层的输入必须是个二维张量

    def forward(self, x):
        # out（当前时间步隐藏变量）的格式：(batch, time_step, hidden_size)
        # h_s（当前时间步隐藏状态）、h_c（记忆细胞）的格式：（n_layer, batch, hidden_size）为最后一个时间步的输出
        # LSTM中前向传播的输入：第一个参数是三维的输入，第二个输入是上个时间步隐藏状态和记忆细胞的初始值
        out, (h_s, h_c) = self.rnn(x.view(-1, 28, 28), None)
        y = self.fc(out[:, -1, :])  # 取最后一个时间步的输出
        return y


rnn = Rnnnet()
for name, param in rnn.named_parameters():
    print(name)
    print(param.size())

第一个参数是输入和遗忘门、输入门、输出门、记忆细胞之间的FC层的weight，FC层上面设置是64个，4个门就是256个，输入是每张图片的一行，是一个由0和1组成的向量，也就是图片的宽度28，因此W：（28， 256），由于nn.Linear的显示是转置过的，因此是（256，28）。bias就是256维的向量。步长T是图片的高28。多对一模型，因此只需要对最后一个时间步的输出做预测。

第二个参数是上个时间步的隐藏变量和遗忘门、输入门、输出门、记忆细胞的FC层的weight，而隐藏变量的大小和FC输出层的大小是一致的（不明白的见上面的细胞结构和公式），故weight：（256，64），bias就是256维的向量。

记忆细胞的运输和当前时间步的隐藏变量计算不需要额外的参数。

输出是10分类，所以是（10， 64），bias是10维的向量。

 

LSTM的forward输入的第二个参数是个元组，就是上个时间步的隐藏状态和记忆细胞的值，写成None，就是将他们归零

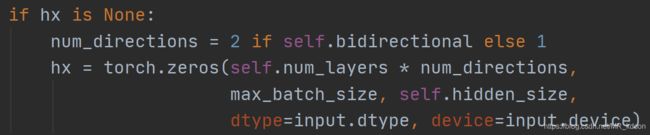
这是底层的实现：可以看出是归零操作，且required_grad=False

 

Q1：LSTM的forward需要输入之前的记忆细胞吗？

在这个MNIST分类任务中是不需要的，因为相邻2个小批量之间不需要有记忆联系，因此forward的第二个参数可以不写，默认为None。但若是相邻2个小批量有记忆联系（比如接下去要讲的cosx回归问题和语言模型中的相邻采样问题），那么forward的第二个参数是要去写一个元组的(h_s,h_s)代表了上个小批量的隐藏状态和记忆细胞。但这里一定得注意的是，必须让这个元组中的2个张量脱离计算图，是为了防止每个iteration串联起来导致梯度计算消耗过大，在每个iteration之间隔断以后，(h_c_hat, h_c)就仅仅只是传递值给下一个iteration而已。

一个iteration表示计算了一个batch的过程，1个epoch里面有多个batch。

Q2：元组(h_s,h_s)的初始化问题

和Q1一样，如果相邻的epoch之间需要有记忆联系（如cosx的回归问题），那么初始化只需要在最开始的时候，令元组为None即可。若相邻的epoch之间不需要有记忆联系（如语言模型中的相邻采样），则只需要在每个epoch开始的时候初始化为None一次就好了。

 

 

4.2、训练结果

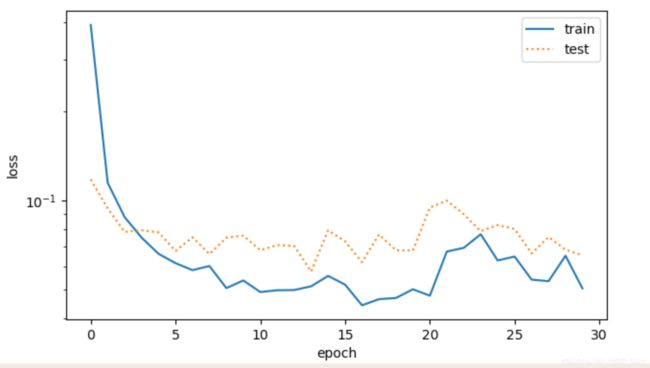
学习率采用0.01，Adam方法，训练30个epoch，每个epoch都会用测试一下loss

 万幸，没有过拟合！

选取最后一个epoch的结果：

分类结果还不错！选取前十张图看看结果：

用LSTM训练分类效果还是不错滴！上面一排数字是label，下面一排数字是prediction。

 

 

五、LSTM用于回归问题

多对多模型

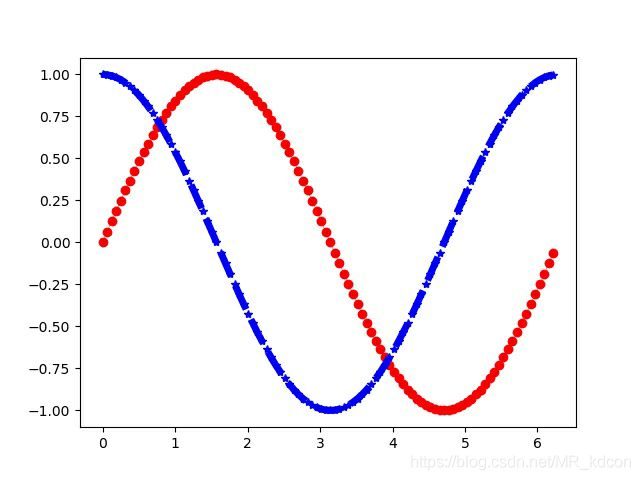
回归问题：这里复现莫凡python中用当前时间点sinx的值来预测cosx的值。是一个实时检测的回归问题。

红色为sinx，蓝色为cosx。

因此我们的损失函数的输入就是用经过sinx做输入的LSTM训练网络的预测结果，和标准的cosx曲线的均方误差。目标函数就是让MSE函数降到很小很小。。。

5.1、同第四部分，直接进入网络部分：

class Rnn(nn.Module):
    def __init__(self):
        super().__init__()
        self.rnn = nn.LSTM(
            input_size=INPUT_SIEZE,
            hidden_size=NEURON_NUM,
            num_layers=1,
            batch_first=True  # (batch, time_step, inputsize)
        )
        self.fc = nn.Linear(32, 1)

    def forward(self, x, state):
        # input (1, 10, 1)
        # out (batch, time_step, hidden_size)
        out, state = self.rnn(x, state)
        t= []
        for i in range(TIME_STEP):
            t.append(self.fc(out[:, i, :]))
        return torch.stack(t, dim=1)  # (batch, time_step, 1)


rnn = Rnn()
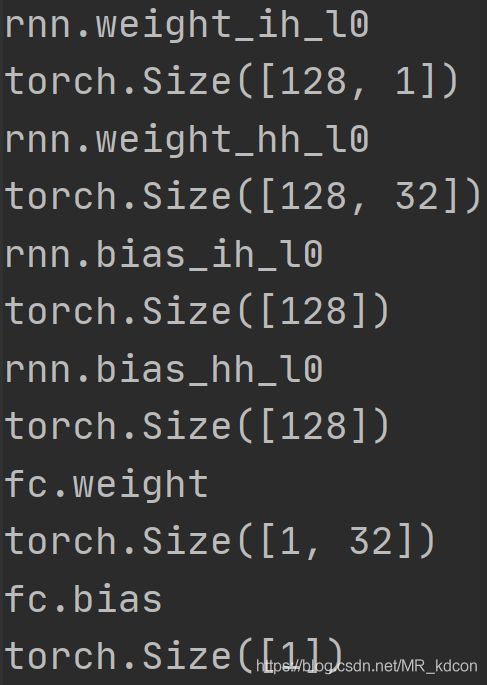
for name, param in rnn.named_parameters():
    print(name)
    print(param.size())

这一部分和分类的结构是基本雷同的。每个细胞的FC层数是1层，32个神经元，输出层是1个神经元，输入格式是(1, 10, 1)，就是batch是1，时间步是10，每个时间步的输入是1个长度。需要注意的是，我们需要时间步10的预测结果进行显示，所以forward方法中就对这10个时间步用list包起来。

网络参数如下：

 第一个weight是输入和4个门的FC层的权重，每个门是32个，4个门就是128个。

第二个weight是上个时间步的隐藏变量和4个门的FC的权重，故（128，32），bias就是128维的向量。

输出是一个值，所以输出层为1。

 

Q1：LSTM的forward需要输入之前的元组吗？

这元组表示(h_s, h_c)。

在这个cosx回归任务中是需要的，因为相邻2个小批量之间需要有记忆联系，因此forward的第二个参数得是上个小批量的最后时间步的元组。但这里一定得注意的是，必须让这个元组脱离计算图，因为一个小批量的数据完成后，生成的最后时间步的隐藏状态将会用来初始化下一小批量的元组。如果不让元组脱离计算图，那么在第二轮小批量完成inference之后，开始反向传播的时候，计算图会去计算之前那个小批量中的梯度，导致梯度计算开销增大。将元组脱离计算图之后，第二个小批量在backward的时候就不会去计算元组的梯度，因为他的required_grad=Flase，根据链式传播原则，后面的梯度就不会继续传了，说的直白点，就是截断了。

并且输入也要带上这个元组。

Q2：元组的初始化问题

和Q1一样，如果相邻的epoch之间需要有记忆联系，那么初始化只需要在最开始的时候，令元组为None即可。若相邻的epoch之间不需要有记忆联系（如语言模型中的相邻采样），则只需要在每个epoch开始的时候初始化为None一次就好了。

 

 

5.2、训练：

5.2.1、相邻批量之间、相邻epoch之间不用记忆联系

lr=0.02，Adam方法，训练100个epoch：

可见拟合效果不是很好，整个过程在GPU上跑了496s。

5.2.2、相邻批量之间、相邻epoch间记忆联系，即当前批量接受来自上个批量最后时间步的(h_s, h_c)

 可见拟合效果很好，整个过程在GPU上跑了191s。

可见记忆的重要性！！！

 

六、RNN实现cosx的实时预测：

多对多模型

6.1、直接进入网络结构：

class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.RNN(
            input_size=INPUT_SIZE,  # 每个时间步的每个个数据的大小
            hidden_size=32,  # 每个细胞中神经元个数
            num_layers=1,  # 每个细胞中FC的层数
            # True：数据格式(batch, time_step, input_size) False：数据格式（time_step, batch, input_size）
            batch_first=True,
        )
        self.fc= nn.Linear(32, 1)

    def forward(self, x, h_state):
        # x (batch, time_step, input_size)  输入格式
        # h_state (n_layers, batch, hidden_size)  最后一步的状态
        # r_out (batch, time_step, hidden_size)  保存了每一步的隐藏状态
        r_out, h_state = self.rnn(x, h_state)

        outs = []  # save all predictions
        for time_step in range(r_out.size(1)):  # calculate output for each time step
            outs.append(self.fc(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state


rnn_layer = RNN()
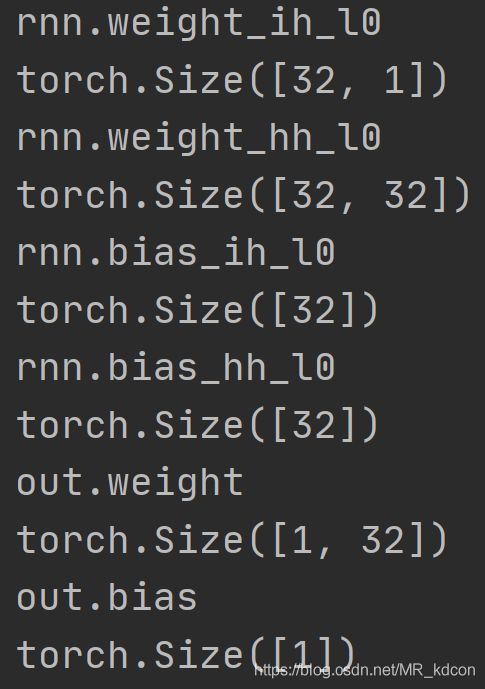
for name, param in rnn_layer.named_parameters():
    print(name)
    print(param.size())

RNN的输入和LSTM是一样的：每一步输入的大小、隐藏层神经元个个数、隐藏层的层数、是否需要改变格式

输出是不一样的，LSTM中第二个输出是包含2个细胞的元组，而RNN中只有一个隐藏变量，用上个时间步的隐藏状态和当前输入来输出当前时间步的隐藏状态，一份用于复制到r_out中，另一份用于给一个时间步的细胞。因此一个RNN下来，h_state保存的是最后一个时间步的隐藏状态。

RNN中forward函数的输入除了X以外，还需要额外的h_state作为初值，输出返回的时候也需要返回最后一个隐藏状态。

参数列表：

参数也和LSTM不一样，具体的：

第一个参数是输入和当前时间步隐藏状态的FC层的weight，输入层只有1个神经元，故（32， 1），bias自然是32维向量。

第二个参数是上个时间步的隐藏状态的FC层的weight，故（32， 32），bias是32维的向量。

输出因为是个预测值，长度为1。

 

RNN的forward函数的第二个输入如果是None，就代表这将h_state归零，且required_grad=Flase.它的底层实现和LSTM是一样的，都继承与RNNBased

 

Q1：RNN的forward需要输入之前的h_state吗？

在这个cosx回归任务中是需要的，因为相邻2个小批量之间需要有记忆联系，因此forward的第二个参数得是上个小批量的最后时间步的隐藏变量。但这里一定得注意的是，必须让这个h_state脱离计算图，因为一个小批量的数据完成后，生成的最后时间步的隐藏状态将会用来初始化下一小批量的h_state。如果不让h_state脱离计算图，那么在第二轮小批量完成inference之后，开始反向传播的时候，计算图会去计算之前那个小批量中的梯度，导致梯度计算开销增大。将h_state脱离计算图之后，第二个小批量在backward的时候就不会去计算h_state的梯度，因为他的required_grad=Flase，根据链式传播原则，后面的梯度就不会继续传了，说的直白点，就是截断了。

Q2：h_state的初始化问题

和Q1一样，如果相邻的epoch之间需要有记忆联系，那么初始化只需要在最开始的时候，令h_state为None即可。若相邻的epoch之间不需要有记忆联系（如语言模型中的相邻采样），则只需要在每个epoch开始的时候初始化为None一次就好了。

 

 

6.2、训练

和LSTM一样，lr=0.02，Adam，训练100个epoch

在gpu上跑了近260s，且拟合效果明显好于LSTM。

因此，一些简单的问题，也许用RNN效果也不比LSTM差多少。 

 

 

 七、深度循环神经网络：

下图是个RNN结构的深度网络，无非就是每个细胞中多加了几个层，上面的实验，我们隐藏层都是1。

同理，当LSTM的每个细胞的隐藏层变多以后，也就是成了深度门控循环神经网络。 

 

 

 

八、RNN实现语言模型预测

主要内容：用一个语言数据集来训练RNN，让这个网络具有创作歌词的能力。是个多对多模型。

其本质就是个分类问题

 

导入数据集->建立数据集合索引的映射->采样并打包成batch->预处理->训练->预测->模型评价

 

8.1、建立字符字典

因为导入的数据集为字符，因此我们需要将其映射成index，即构建一个字符字典，字典的长度为不同字的种类数目，也就是我们分类的总类别数目。

 

8.2、采样并打包成batch

和之前的采样不同，语言模型的采样必须是一个时间步内连续的字符，比如时间步为5的输入是 “我要去打篮”，其标签为数据集中的下一个字，“要去打篮球”。

采样一共2种方式，一种是随机采样，另一种是相邻采样：

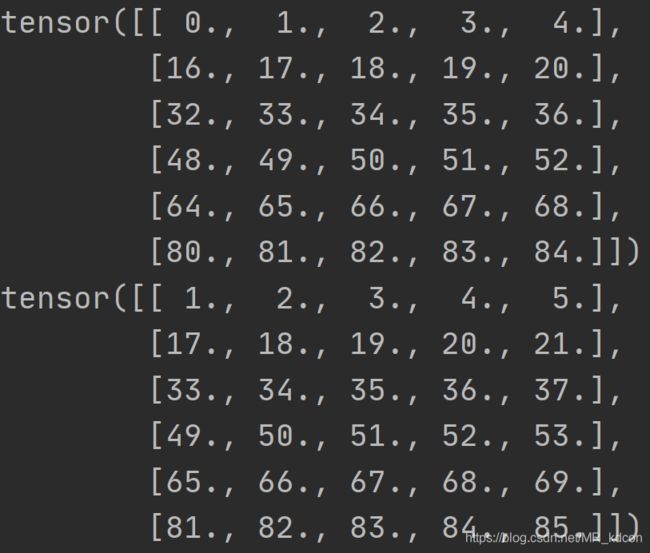
8.2.1、随机采样

在随机采样中，每个样本是原始序列上任意截取的⼀段序列。相邻的两个随机小批量在原始序列上的位置不⼀定相毗邻。因此，我们无法用⼀个小批量最终时间步的隐藏状态来初始化下⼀个小批量的隐藏状态。 在训练模型时，每次随机采样前，或者说下一个小批量更新之前，都需要重新初始化隐藏状态。用None来初始化，也可以起到截断h_state的requires_grad的作用。

 

比如我现在设置batch=10，输入的字符字典是[0,1,2...99]，时间步长T=5，随机采样的效果：

 

可见采样的数据X,Y：（batch，time_step）、（batch，time_step）

 

 

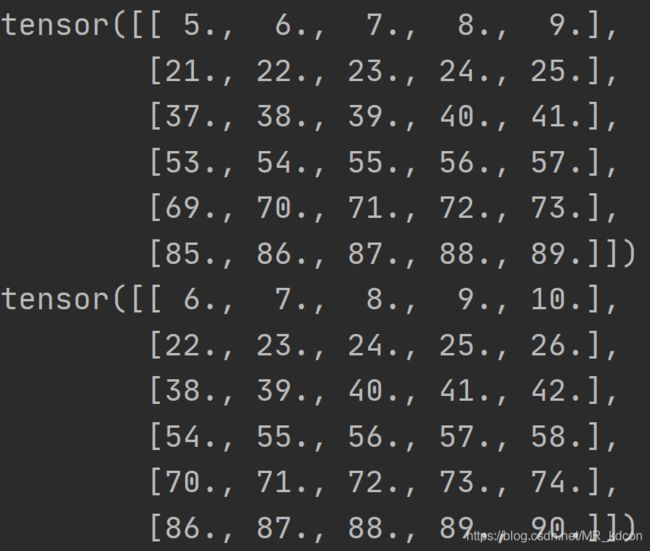
8.2.2:相邻采样

令相邻的两个随机小批量在原始序列上的位置相毗邻。这时候，我们就可以⽤⼀个小批量最终时间步的隐藏状态来初始化下⼀个小批量的隐藏状态，从而使下⼀个⼩批量的输出也取决于当前小批量的输入，并如此循环下去。

 

比如设置batchsize=6，time_step=5，输入字符字典[0,1,2,....99]，相邻采样结果：

 

这对实现循环神经网络造成了两⽅⾯影响：一方面， 在训练模型时，我们 只需在每⼀个epoch开始时初始化隐藏状态 ；另⼀⽅面，当多个相邻⼩批量通过传递隐藏状态串联起来时，模型参数的梯度计算将依赖所有串联起来的⼩批量序列。同⼀epoch中，随着迭代次数的增加，梯度的计算开销会越来越⼤。 为了使模型参数的梯度计算只依赖⼀次迭代读取的⼩批量序列， 我们可以在每次读取小批量前将隐藏状态从计算图中分离出来。

 

 

8.3、预处理

这是个分类问题，参考上面的MNIST分类问题，他的输入是个向量，因此这里我们也可以将输入表示成向量，最简单的方式就是转为one-hot形式。即（batch，time_step）--->列表list，列表的长度为time_step的大小，列表的每个元素是一个（batch，dict_num）的张量，dict_num就是字符字典的大小。

这样会有3个问题

Q1：RNN网络的输入为3维的向量，该怎么办呢？其实简单的，用torch.stack进行堆叠即可，最后成（batch，time_step，input_num=dict_num）。

Q2：怎么转为one-hot向量呢？就是用pythorch提供的scatter函数

（不懂scatter的可以参考https://blog.csdn.net/MR_kdcon/article/details/108900039第4.1节）

具体的，就是对于每个时间步的batch个数据用scatter填充为（batch，dict_num）格式的张量。

Q3：一定要转为one-hot形式吗？不一定，2种输入格式均可。

 

8.4、训练模型

8.4.1、梯度裁剪

RNN中易出现梯度消失和梯度爆炸，为了预防这个，我们采用梯度裁剪

，裁剪后的梯度的L2范数小于

 

8.4.2、损失函数

由于这个本质是个分类问题，且是多对多模型，所以每个时间步的输出接softmax，crossentropy损失函数。

 

8.5、预测

预测的时候，我们给定几个字符，如‘我要’，然后输入进我们的网络作为第一时间步和第二时间步的输入，每次吐出一个字符以及当前时间步的h_state，作为下个时间步的输入

预测结果：
给定['分开', '不分开']

这里的perplexity是模型评价指标-困惑度 

模型评价指标：困惑度

其中：指数为e。 

可见困惑度在持续下降，意味着分类能力会越强，我们的输出歌词会更流畅。

 

 

九、LSTM实现语言模型

LSTM的实现方式和RNN几乎没差别，只是网络有差异，LSTM在输出上多了一个记忆细胞的输出。

流程也一模一样：
导入数据集->建立字符和索引的映射->采样并批量化->数据预处理（one-hot）->训练->预测->模型评价

直接预测结果：

 

感觉LSTM写的更加JAY，hhhhhh 

 

 

十、实战中的注意点

1、one-hot向量不仅可以用于输出端的标签，也可以用于时输入端的特征。

2、有时候我们需要切断计算图中不相关变量的required_grad，除了为了避免计算图中的梯度计算收到干扰，另一个重要原因是为了节约梯度计算资源。这两点在后续强化学习中也尤为重要，特别是策略网络对于动作的选择、Target网络选择TD目标值等。