Java数据结构——平衡二叉树(AVL树)

AVL树的引入

搜索二叉树有着极高的搜索效率，但是搜索二叉树会出现以下极端情况：

这样的二叉树搜索效率甚至比链表还低。在搜索二叉树基础上出现的平衡二叉树(AVL树)就解决了这样的问题。当平衡二叉树(AVL树)的某个节点左右子树高度差的绝对值大于1时，就会通过旋转操作减小它们的高度差。

基本概念

AVL树本质上还是一棵二叉搜索树，它的特点是：

1. 本身首先是一棵二叉搜索树。
2. 每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。
3. 当插入一个节点或者删除一个节点时，导致某一个节点的左右子树高度差的绝对值大于1，这时需要通过左旋和右旋的操作使二叉树再次达到平衡状态。

平衡因子(balanceFactor)

• 一个结点的左子树与右子树的高度之差。
• AVL树中的任意结点的BF只可能是-1，0和1。

基础设计

下面是AVL树需要的简单方法和属性：

public class AVLTree <E extends Comparable<E>>{
    class Node{
        E value;
        Node left;
        Node right;
        int height;
        public Node(){}
        public Node(E value){
            this.value = value;
            height = 1;
            left = null;
            right = null;
        }
        public void display(){
            System.out.print(this.value + " ");
        }
    }
    Node root;
    int size;
    public int size(){
        return size;
    }
    public int getHeight(Node node) {
        if(node == null) return 0;
        return node.height;
    }
    //获取平衡因子(左右子树的高度差，大小为1或者0是平衡的，大小大于1不平衡)
    public int getBalanceFactor(){
        return getBalanceFactor(root);
    }
    public int getBalanceFactor(Node node){
        if(node == null) return 0;
        return getHeight(node.left) - getHeight(node.right);
    }

    //判断一个树是否是一个平衡二叉树
    public boolean isBalance(Node node){
        if(node == null) return true;
        int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
        if(balanceFactor > 1) return false;
        return isBalance(node.left) && isBalance(node.right);
    }
    public boolean isBalance(){
        return isBalance(root);
    }

    //中序遍历树
    private  void inPrevOrder(Node root){
        if(root == null) return;
        inPrevOrder(root.left);
        root.display();
        inPrevOrder(root.right);
    }
    public void inPrevOrder(){
        System.out.print("中序遍历：");
        inPrevOrder(root);
    }
}

RR(左旋)

往一个树右子树的右子树上插入一个节点，导致二叉树变得不在平衡，如下图，往平衡二叉树中插入5，导致这个树变得不再平衡，此时需要左旋操作，如下：

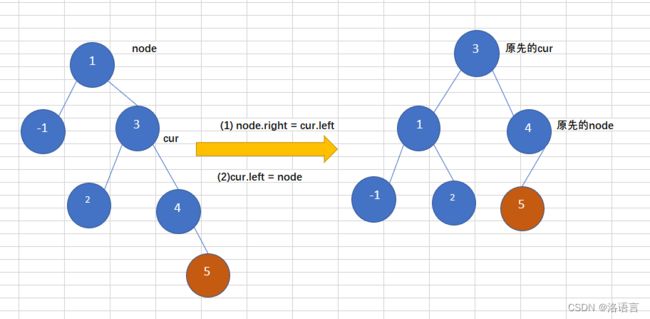
代码如下：

//左旋,并且返回新的根节点
    public Node leftRotate(Node node){
        System.out.println("leftRotate");
       Node cur = node.right;
       node.right = cur.left;
       cur.left = node;
       //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LL(右旋)

往一个AVL树左子树的左子树上插入一个节点，导致二叉树变得不在平衡，如下图，往平衡二叉树中插入2，导致这个树变得不再平衡，此时需要左旋操作，如下：

代码如下：

 //右旋，并且返回新的根节点
    public Node rightRotate(Node node){
        System.out.println("rightRotate");
        Node cur = node.left;
        node.left = cur.right;
        cur.right = node;
        //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LR(先左旋再右旋)

往AVL树左子树的右子树上插入一个节点，导致该树不再平衡，需要先对左子树进行左旋，再对整棵树右旋，如下图所示，插入节点为5.

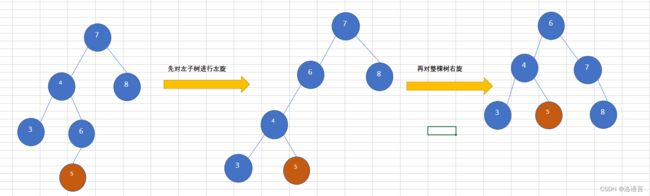
RL(先右旋再左旋)

往AVL树右子树的左子树上插入一个节点，导致该树不再平衡，需要先对右子树进行右旋，再对整棵树左旋，如下图所示，插入节点为2.

添加节点

//添加元素
    public  void add(E e){
        root = add(root,e);
    }
    public Node add(Node node, E value) {
        if (node == null) {
            size++;
            return new Node(value);
        }
        if (value.compareTo(node.value) > 0) {
            node.right = add(node.right, value);
        } else if (value.compareTo(node.value) < 0) {
            node.left = add(node.left, value);
        }
        //跟新节点高度
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        //获取当前节点的平衡因子
        int balanceFactor = getBalanceFactor(node);
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上，此时需要进行右旋
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上，此时需要先对左子树左旋，在整个树右旋
        else if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        //balanceFactor < -1 && getBalanceFactor(node.left) > 0
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上，此时需要先对右子树右旋，再整个树左旋
        else if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

删除节点

 //删除节点
    public E remove(E value){
        root = remove(root,value);
        if(root == null){
            return null;
        }
        return root.value;
    }
    public Node remove(Node node, E value){
        Node retNode = null;
        if(node == null)
            return retNode;
        if(value.compareTo(node.value) > 0){
            node.right = remove(node.right,value);
            retNode = node;
        }
        else if(value.compareTo(node.value) < 0){
            node.left = remove(node.left,value);
            retNode = node;
        }
        //value.compareTo(node.value) = 0
        else{
            //左右节点都为空，或者左节点为空
            if(node.left == null){
                size--;
                retNode = node.right;
            }
            //右节点为空
            else if(node.right == null){
                size--;
                retNode = node.left;
            }
            //左右节点都不为空
            else{
                Node successor = new Node();
                //寻找右子树最小的节点
                Node cur = node.right;
                while(cur.left != null){
                    cur = cur.left;
                }
                successor.value  = cur.value;
                successor.right = remove(node.right,value);
                successor.left = node.left;
                node.left =  node.right = null;
                retNode = successor;
            }
            if(retNode == null)
                return null;
            //维护二叉树平衡
            //跟新height
            retNode.height = Math.max(getHeight(retNode.left),getHeight(retNode.right));
        }
        int balanceFactor = getBalanceFactor(retNode);
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上，此时需要进行右旋
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
            return leftRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上，此时需要先对左子树左旋，在整个树右旋
        else if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上，此时需要先对右子树右旋，再整个树左旋
        else if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return  retNode;
    }