八大数据结构——平衡二叉树(七)
八大数据结构——平衡二叉树(七)
目录
-
- 八大数据结构——平衡二叉树(七)
- 二叉树的旋转
- Java代码实现
- 完整代码
树是数据结构中非常重要的一项,有关树的数据结构有许多种,本文重点研究的是平衡二叉树,并且在二叉搜索树的基础上写的,如果不了解二叉搜索树,请移步 二叉搜索树。
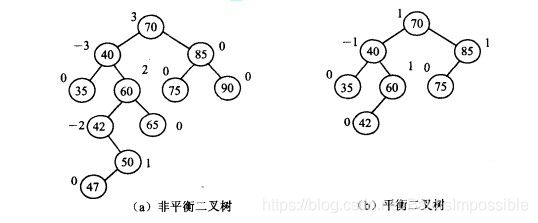
平衡二叉树定义:
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。
特点:
1.本身首先是一棵二叉搜索树。
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
优点:
1.有链表的快速插入与删除操作的特点。
2.又有数组快速查找的优势。
3.克服了二叉搜索树可能退化成链表的缺点。
缺点:
1.二叉搜索树的构造与插入顺序有关。
2.某种程度上,增加了插入和删除的时间,因为增减节点后都要调整,使其重新满足平衡条件。
适用场景:
大量数据的存储和操作。它的构建,插入,删除,查询的复杂度都稳定在O( log 2 \log_2 log2N)。
二叉树的旋转
平衡二叉树其他方面与二叉搜索树类似,只是在此基础上增加了调整平衡的方案。
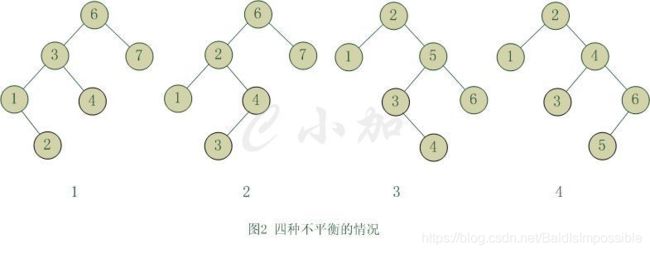
平衡二叉树不平衡的情形:
把需要重新平衡的结点叫做α,由于任意两个结点最多只有两个儿子,因此高度不平衡时,α结点的两颗子树的高度相差2.容易看出,这种不平衡可能出现在下面4中情况中:
1.对α的左儿子的左子树进行一次插入
2.对α的左儿子的右子树进行一次插入
3.对α的右儿子的左子树进行一次插入
4.对α的右儿子的右子树进行一次插入
第一种情况是插入发生在“外边”的情形(左左或右右),该情况可以通过一次单旋转完成调整;第二种情况是插入发生在“内部”的情形(左右或右左),这种情况比较复杂,需要通过双旋转来调整。
调整措施:
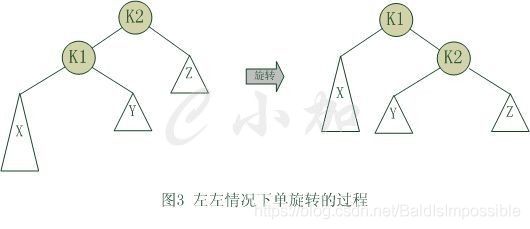
一、单旋转
上图是左左的情况,k2结点不满足平衡性,它的左子树k1比右子树z深两层,k1子树中更深的是k1的左子树x,因此属于左左情况。
为了恢复平衡,我们把x上移一层,并把z下移一层,但此时实际已经超出了AVL树的性质要求。为此,重新安排结点以形成一颗等价的树。为使树恢复平衡,我们把k2变成这棵树的根节点,因为k2大于k1,把k2置于k1的右子树上,而原本在k1右子树的Y大于k1,小于k2,就把Y置于k2的左子树上,这样既满足了二叉查找树的性质,又满足了平衡二叉树的性质。
这种情况称为单旋转。
二、双旋转
对于左右和右左两种情况,单旋转不能解决问题,要经过两次旋转。
对于上图情况,为使树恢复平衡,我们需要进行两步,第一步,把k1作为根,进行一次右右旋转,旋转之后就变成了左左情况,所以第二步再进行一次左左旋转,最后得到了一棵以k2为根的平衡二叉树。
Java代码实现
下面通过Java来实现一个平衡二叉树,基于jdk1.8。
1.首先把树节点定义出来。
class BSTNode<T extends Comparable>{
public T val;//存储数据
public BSTNode<T> leftNode;//左子节点
public BSTNode<T> rightNode;//右子节点
}
2.定义平衡二叉树的属性。
private BSTNode<T> root;//根节点
private int size;//记录已存储元素个数
3.构造方法和一些常用方法。
public AvlTree() {
root = null;
size = 0;
}
public AvlTree(T val) {
root = new BSTNode<>();
root.val = val;
size = 1;
}
public boolean isEmpty() {
return size == 0;
}
public int size() {
return size;
}
4.查询操作。查询从根节点开始,通过不断比较一直往下走,大于当前节点就往右子树的方向走,小于当前节点就往左子树的方向走。
private BSTNode<T> find(T val) {
if (root == null || val == null) {
return null;
}
BSTNode<T> node = root;
while (node != null) {
if (node.val.compareTo(val) == 0) {
return node;
} else if (node.val.compareTo(val) > 0) {
node = node.leftNode;
} else {
node = node.rightNode;
}
}
return null;
}
private BSTNode<T> parent(BSTNode<T> current) {
if (root == null || current == null) {
return null;
}
BSTNode<T> node = root;
while (node != null) {
if (node.leftNode == current || node.rightNode == current) {
return node;
} else if (node.val.compareTo(current.val) > 0) {
node = node.leftNode;
} else {
node = node.rightNode;
}
}
return null;
}
// 查询
public boolean contain(T val) {
return find(val) != null;
}
5.因为我们需要判断二叉树是否平衡,所以需要使用到二叉树的深度,需要定义一个方法,来求深度。
// 获取该节点的深度
private int depth(BSTNode<T> node) {
if (node == null) {
return 0;
}
int left = depth(node.leftNode);
int right = depth(node.rightNode);
return left >= right ? left + 1 : right + 1;
}
6.在进行调整操作前,我们需要确定是否存在不平衡点,且不平衡点在哪。我们从最近增加或删除的节点出发,开始往其父节点方向查询。
// 查找不平衡节点,参数node为刚插入节点的父节点,从下往上找不平衡节点
private BSTNode<T> NoAvlNode(BSTNode<T> node) {
if (node == null) {
return null;
} else if (Math.abs(depth(node.leftNode) - depth(node.rightNode)) > 1) {
return node;
} else {
return NoAvlNode(parent(node));
}
}
7.定义四个情况下的旋转调整方法,需要注意的是,左左和右右方法中,在其子节点代替了其父节点后,要去调整其父节点的父节点,相当于告诉它:“现在由我来当你的子节点!”。
双旋转只需去调用单旋转:
1.左右,先右右,再左左。
2.右左,先左左,再右右。
// 修改父节点的左右子节点指针
private void adjustParent(BSTNode<T> node,BSTNode<T> child){
BSTNode<T> parent = parent(node);
if(parent==null){return;}
if(parent.leftNode!=null&&parent.leftNode==node){
parent.leftNode = child;
}else {
parent.rightNode = child;
}
}
// 左左旋转,参数node为不平衡节点
// 左左情况下,node的左子节点肯定不能为null
private void LL(BSTNode<T> node) {
if (node == null) {
return;
}
BSTNode<T> leftNode = node.leftNode;
node.leftNode = leftNode.rightNode;
leftNode.rightNode = node;
// 如果原本的不平衡节点是根节点,那么旋转后要修改根节点的引用
if (root == node) {
root = leftNode;
}else {
adjustParent(node,leftNode);
}
}
// 右右旋转
// 右右情况下,node的右子节点肯定不能为null
private void RR(BSTNode<T> node) {
if (node == null) {
return;
}
BSTNode<T> rightNode = node.rightNode;
node.rightNode = rightNode.leftNode;
rightNode.leftNode = node;
if (root == node) {
root = rightNode;
}else {
adjustParent(node,rightNode);
}
}
// 左右旋转,先右右,再左左
private void LR(BSTNode<T> node) {
if (node == null) {
return;
}
RR(node.leftNode);
LL(node);
}
// 右左旋转,先左左,再右右
private void RL(BSTNode<T> node) {
if (node == null) {
return;
}
LL(node.rightNode);
RR(node);
}
8.确定不平衡情况是4种中的哪一种。我们通过两次对比左右子树的深度,就可以了。我们可以这么理解左左,右右这些含义:
1.左左,第一个左,不平衡节点的左子树深度大;第二个左,不平衡节点的左子节点的左子树深度大。
2.左右,第一个左,不平衡节点的左子树深度大;第二个右,不平衡节点的左子节点的右子树深度大。
3.右左,第一个右,不平衡节点的右子树深度大;第二个左,不平衡节点的右子节点的左子树深度大。
4.右右,第一个右,不平衡节点的右子树深度大;第二个右,不平衡节点的右子节点的右子树深度大。
// 调整树结构,使其达到平衡,参数node为刚插入节点的父节点
private void adjust(BSTNode<T> node) {
BSTNode<T> noAvlNode = NoAvlNode(node);
if (noAvlNode == null) {
return;
}
if (depth(noAvlNode.leftNode) > depth(noAvlNode.rightNode)) {
// 左子树深度大于右子树深度
if (depth(noAvlNode.leftNode.leftNode) >
depth(noAvlNode.leftNode.rightNode)) {
// 左左情况
LL(noAvlNode);
} else {
// 左右情况
LR(noAvlNode);
}
} else {
// 右子树深度大于左子树深度
if (depth(noAvlNode.rightNode.leftNode) >
depth(noAvlNode.rightNode.rightNode)) {
// 右左情况
RL(noAvlNode);
} else {
// 右右情况
RR(noAvlNode);
}
}
}
9.插入操作,和二叉搜索树的插入操作一样,只是插入完后,调用一下调整方法,确保保持平衡,传入的参数就是刚插入节点的父节点。
// 插入数据
public boolean insert(T val) {
// 如果val为null直接返回
if (val == null) {
return false;
}
// 如果root为null,那新建一个节点,并让保存为root
if (root == null) {
root = new BSTNode<>();
root.val = val;
size++;
return true;
}
// root不为null,那就通过循环找到正确的插入位置
BSTNode<T> node = root;
while (true) {
// 如果val与已有值相等,则不允许插入
if (node.val.compareTo(val) == 0) {
return false;
}
// val值小于当前节点,则插入到左子树
if (node.val.compareTo(val) > 0) {
// 如果左子节点为空,则插入到此处
if (node.leftNode == null) {
BSTNode<T> leftNode = new BSTNode<>();
leftNode.val = val;
node.leftNode = leftNode;
size++;
adjust(node);
return true;
} else {
// 不为空继续往下找
node = node.leftNode;
}
// val值大于当前节点,则插入到右子数
} else {
// 如果右子节点为空,则插入到此处
if (node.rightNode == null) {
BSTNode<T> rightNode = new BSTNode<>();
rightNode.val = val;
node.rightNode = rightNode;
size++;
adjust(node);
return true;
} else {
// 不为空继续往下找
node = node.rightNode;
}
}
}
}
10.删除操作,删除操作和二叉搜索树的删除操作一样。也是删除完后要调用调整方法。但是参数有两种情况:
1.度为1或0的删除,它们自己这个位置已经被干掉了,所以参数应该是其父节点。
2.度为2的删除,它自己是替换了值,真正被干掉的是他的左子树中的一个叶子节点,所以此时参数应该是它自己。
// 删除数据
public boolean remove(T val) {
// 先通过循环找到要删除的节点
BSTNode<T> node = root;
while (node != null && node.val.compareTo(val) != 0) {
if (node.val.compareTo(val) > 0) {
node = node.leftNode;
} else if (node.val.compareTo(val) < 0) {
node = node.rightNode;
}
}
// 如果找不到则返回false
if (node == null) {
return false;
}
// 要删除的节点有三种情况,度为2,度为1和度为0的
if (node.leftNode != null && node.rightNode != null) {
// 度为2的节点,删除步骤为
// 1.找到要删除节点的左子数中最大节点。
// 2.替换待删除节点的值为这个最大节点值
// 3.将这个最大节点删除
BSTNode<T> maxNode = node.leftNode;
while (maxNode.rightNode != null) {
maxNode = maxNode.rightNode;
}
remove(maxNode.val);
node.val = maxNode.val;
// 删除完成后,实际上是要删除节点的左子树深度发生改变,此时以要删除节点的位置开始,去查找并调整树
adjust(node);
} else {
// 度为1和度为2的节点一起处理,分两种情况。
// 1.要删除的节点为根节点。
// 2.要删除的节点为非根节点。
BSTNode<T> parent = parent(node);
BSTNode<T> child =
node.leftNode == null ? node.rightNode : node.leftNode;
// 根节点无父节点,直接将根节点指向子节点即可。
if (parent == null) {
root = child;
} else {
// 非根节点,找到它是父节点的左子节点,还是右子节点,然后通过修改父节点指针即可。
adjustParent(node,child);
}
// 删除完成后,要删除的节点已经不存在了,实际上是要删除节点的父节点,的左子树或右子树深度发生改变,
// 此时以要删除节点的父节点的位置开始,去查找并调整树
adjust(parent);
}
size--;
return true;
}
完整代码
//平衡二叉树
public class AvlTree<T extends Comparable> {
private BSTNode<T> root;//根节点
private int size;//记录已存储元素个数
private BSTNode<T> find(T val) {
if (root == null || val == null) {
return null;
}
BSTNode<T> node = root;
while (node != null) {
if (node.val.compareTo(val) == 0) {
return node;
} else if (node.val.compareTo(val) > 0) {
node = node.leftNode;
} else {
node = node.rightNode;
}
}
return null;
}
private BSTNode<T> parent(BSTNode<T> current) {
if (root == null || current == null) {
return null;
}
BSTNode<T> node = root;
while (node != null) {
if (node.leftNode == current || node.rightNode == current) {
return node;
} else if (node.val.compareTo(current.val) > 0) {
node = node.leftNode;
} else {
node = node.rightNode;
}
}
return null;
}
// 获取该节点的深度
private int depth(BSTNode<T> node) {
if (node == null) {
return 0;
}
int left = depth(node.leftNode);
int right = depth(node.rightNode);
return left >= right ? left + 1 : right + 1;
}
// 查找不平衡节点,参数node为刚插入节点的父节点,从下往上找不平衡节点
private BSTNode<T> NoAvlNode(BSTNode<T> node) {
if (node == null) {
return null;
} else if (Math.abs(depth(node.leftNode) - depth(node.rightNode)) > 1) {
return node;
} else {
return NoAvlNode(parent(node));
}
}
// 修改父节点的左右子节点指针
private void adjustParent(BSTNode<T> node,BSTNode<T> child){
BSTNode<T> parent = parent(node);
if(parent==null){return;}
if(parent.leftNode!=null&&parent.leftNode==node){
parent.leftNode = child;
}else {
parent.rightNode = child;
}
}
// 左左旋转,参数node为不平衡节点
// 左左情况下,node的左子节点肯定不能为null
private void LL(BSTNode<T> node) {
if (node == null) {
return;
}
BSTNode<T> leftNode = node.leftNode;
node.leftNode = leftNode.rightNode;
leftNode.rightNode = node;
// 如果原本的不平衡节点是根节点,那么旋转后要修改根节点的引用
if (root == node) {
root = leftNode;
}else {
adjustParent(node,leftNode);
}
}
// 右右旋转
// 右右情况下,node的右子节点肯定不能为null
private void RR(BSTNode<T> node) {
if (node == null) {
return;
}
BSTNode<T> rightNode = node.rightNode;
node.rightNode = rightNode.leftNode;
rightNode.leftNode = node;
if (root == node) {
root = rightNode;
}else {
adjustParent(node,rightNode);
}
}
// 左右旋转,先右右,再左左
private void LR(BSTNode<T> node) {
if (node == null) {
return;
}
RR(node.leftNode);
LL(node);
}
// 右左旋转,先左左,再右右
private void RL(BSTNode<T> node) {
if (node == null) {
return;
}
LL(node.rightNode);
RR(node);
}
// 调整树结构,使其达到平衡,参数node为刚插入节点的父节点
private void adjust(BSTNode<T> node) {
BSTNode<T> noAvlNode = NoAvlNode(node);
if (noAvlNode == null) {
return;
}
if (depth(noAvlNode.leftNode) > depth(noAvlNode.rightNode)) {
// 左子数深度大于右子数深度
if (depth(noAvlNode.leftNode.leftNode) >
depth(noAvlNode.leftNode.rightNode)) {
// 左左情况
LL(noAvlNode);
} else {
// 左右情况
LR(noAvlNode);
}
} else {
// 右子数深度大于左子数深度
if (depth(noAvlNode.rightNode.leftNode) >
depth(noAvlNode.rightNode.rightNode)) {
// 右左情况
RL(noAvlNode);
} else {
// 右右情况
RR(noAvlNode);
}
}
}
public AvlTree() {
root = null;
size = 0;
}
public AvlTree(T val) {
root = new BSTNode<>();
root.val = val;
size = 1;
}
public boolean isEmpty() {
return size == 0;
}
public int size() {
return size;
}
// 返回父节点的值
public T parent(T val) {
BSTNode<T> node = parent(find(val));
return node == null ? null : node.val;
}
// 返回左子节点的值
public T leftNode(T val) {
BSTNode<T> node = find(val);
return node != null && node.leftNode != null ? node.leftNode.val : null;
}
// 返回右子节点的值
public T rightNode(T val) {
BSTNode<T> node = find(val);
return node != null && node.rightNode != null ? node.rightNode.val :
null;
}
// 返回根节点的值
public T getRoot() {
return root == null ? null : root.val;
}
// 插入数据
public boolean insert(T val) {
// 如果val为null直接返回
if (val == null) {
return false;
}
// 如果root为null,那新建一个节点,并让保存为root
if (root == null) {
root = new BSTNode<>();
root.val = val;
size++;
return true;
}
// root不为null,那就通过循环找到正确的插入位置
BSTNode<T> node = root;
while (true) {
// 如果val与已有值相等,则不允许插入
if (node.val.compareTo(val) == 0) {
return false;
}
// val值小于当前节点,则插入到左子树
if (node.val.compareTo(val) > 0) {
// 如果左子节点为空,则插入到此处
if (node.leftNode == null) {
BSTNode<T> leftNode = new BSTNode<>();
leftNode.val = val;
node.leftNode = leftNode;
size++;
adjust(node);
return true;
} else {
// 不为空继续往下找
node = node.leftNode;
}
// val值大于当前节点,则插入到右子数
} else {
// 如果右子节点为空,则插入到此处
if (node.rightNode == null) {
BSTNode<T> rightNode = new BSTNode<>();
rightNode.val = val;
node.rightNode = rightNode;
size++;
adjust(node);
return true;
} else {
// 不为空继续往下找
node = node.rightNode;
}
}
}
}
// 删除数据
public boolean remove(T val) {
// 先通过循环找到要删除的节点
BSTNode<T> node = root;
while (node != null && node.val.compareTo(val) != 0) {
if (node.val.compareTo(val) > 0) {
node = node.leftNode;
} else if (node.val.compareTo(val) < 0) {
node = node.rightNode;
}
}
// 如果找不到则返回false
if (node == null) {
return false;
}
// 要删除的节点有三种情况,度为2,度为1和度为0的
if (node.leftNode != null && node.rightNode != null) {
// 度为2的节点,删除步骤为
// 1.找到要删除节点的左子数中最大节点。
// 2.替换待删除节点的值为这个最大节点值
// 3.将这个最大节点删除
BSTNode<T> maxNode = node.leftNode;
while (maxNode.rightNode != null) {
maxNode = maxNode.rightNode;
}
remove(maxNode.val);
node.val = maxNode.val;
// 删除完成后,实际上是要删除节点的左子树深度发生改变,此时以要删除节点的位置开始,去查找并调整树
adjust(node);
} else {
// 度为1和度为2的节点一起处理,分两种情况。
// 1.要删除的节点为根节点。
// 2.要删除的节点为非根节点。
BSTNode<T> parent = parent(node);
BSTNode<T> child =
node.leftNode == null ? node.rightNode : node.leftNode;
// 根节点无父节点,直接将根节点指向子节点即可。
if (parent == null) {
root = child;
} else {
// 非根节点,找到它是父节点的左子节点,还是右子节点,然后通过修改父节点指针即可。
adjustParent(node,child);
}
// 删除完成后,要删除的节点已经不存在了,实际上是要删除节点的父节点,的左子树或右子树深度发生改变,
// 此时以要删除节点的父节点的位置开始,去查找并调整树
adjust(parent);
}
size--;
return true;
}
// 查询
public boolean contain(T val) {
return find(val) != null;
}
}
class BSTNode<T extends Comparable>{
public T val;//存储数据
public BSTNode<T> leftNode;//左子节点
public BSTNode<T> rightNode;//右子节点
}