看完必会的回溯算法入门攻略，丈母娘看了都说好

这是一篇关于回溯算法的「详细的入门级攻略」（真的就只是「入门级」）。

回溯的含义

「回溯」本质上是「搜索的一种方式」，一般情况下，该搜索指「深度优先搜索（dfs）」。且实现上使用「递归」的方式。

从“全排列”开始

全排列是回溯最经典的应用之一，我们以全排列做基本示例，先来理解最简单的回溯是如何执行的。

LeetCode 46. 全排列

（参考力扣的46题：https://leetcode-cn.com/problems/permutations/）

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入样例

3

输出样例

1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1

解释：输入样例为输入的整数n。输出样例为1~n的三个数字(1,2,3)的所有排列方式。

简单的思路

先把这道题当做脑筋急转弯，我们很容易就可以想到简单的思路：「分别把不同的数字放到每个位置上」。

例如：

1. 1 2 3，总共三个数，所以有三个位置，我们把1放在第一个位置，那么第二个位置可以放2或3，无论第二个位置放哪一个，第三个位置都只能放另外一个，而当三个位置都放完就找到了一个完整的排列方法；
2. 以此类推的，如果第一个位置放2，那么第二个位置有两种放置方式；
3. 如果第一个位置放3，那么第二个位置同样有两种放置方式；
4. 我们把这一放置的过程用可视化图形表达出来，会形成一种树的形式：

回溯是在做什么？

请仔细研究一下上面的放置思路，其中有一个隐藏的关键点：「从第一层向下搜索到第三层，找到一个结果之后，需要重新回到第一层；再从第一层延伸到第二层的其他分支。」也就是说，需要「沿着如下图的红色箭头指向顺序搜索」。

想要用代码实现这一搜索过程，这一关键点是需要想清楚的：「如何在搜索出一个结果之后，让代码可以往回搜索呢？」

Code

「往回搜索」其实就是回溯的过程，先来看下全排列中的代码实现：

class Solution {
public:
    vector> res; // 存储所有排列方法
    vector st; // 存储数字是否被用过
    vector path; // 存储当前排列方法
    // 使用递归的实现搜索，其中u表示当前已经排列的个数
    void dfs(int u, vector& nums) {
        // 如果已经排列的数字个数和总数字个数相等，说明已经完成一次排列
        // 把当前的排列方法放入最终结果，并return。
        if (u == nums.size()) {        //  ①
            res.push_back(path);       //  ②
            return;                    //  ③
        }
        // 枚举数字
        for (int i = 0; i < nums.size(); i ++ ) {  // ④
            // 没有使用过的数字参与排列
            if (!st[i]) {                  //  ⑤
                path.push_back(nums[i]);   //  ⑥
                st[i] = true;              //  ⑦
                dfs(u + 1, nums);          //  ⑧
                st[i] = false;             //  ⑨
                path.pop_back();           //  ⑩
            }
        }
    }
    vector> permute(vector& nums) {
        for (int i = 0; i < nums.size(); i ++ ) st.push_back(false);
        dfs(0, nums);
        return res;
    }
};

---

「接下来是本文重中之重，我们来看一下上面的代码的完整的执行流程，以此来了解为何这样写就能完成回溯。」

1. 首先，要明确的几个关键角色：u: 可以理解为“目前使用了几个数字”、“目前处于树的第几层”等等；res: 保存最终结果（所有路径）；path: 保存当前的路径，保存的是值，比如nums[0],nums[1]等；st（state）: 存储数字是否被使用过，上面代码直接存储的下标（也可以存储值），因此下面分析中st也是以下标为准；nums: 数组，既保存需要排列的数字，如n=3,nums=[1,2,3]。
2. 明确递归函数的含义，递归函数最重要的就是其表达的含义，而在上面代码中，递归函数dfs的含义是「深度优先搜索，当搜索到一个结果之后，就把结果加入到结果res」。
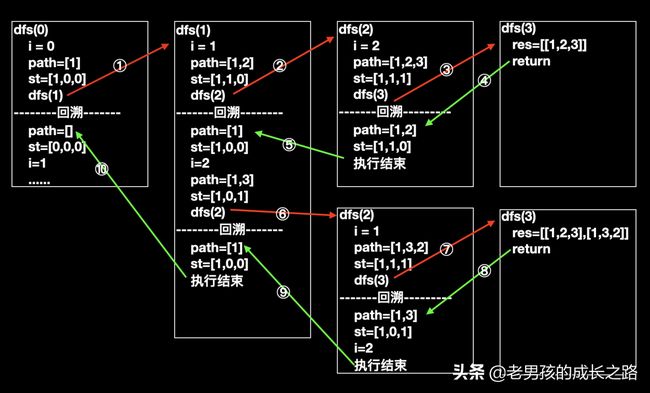
3. 「最最最最重要的」，我们来看一下回溯的执行过程：

1. 「最最最最重要的」，执行过程中的全部变化如下：

1. 从图中path的变化，可以明显的看出，其实代码的执行顺序正好对应了上面图中的搜索顺序。
2. 理解回溯（或者说递归），至关重要的一点：「当一个函数让出执行权后，执行权又重新回来，函数当前的变量状态应该和让出前一致。」以上面的dfs(1)为例，在第②步(不是代码②)，递归到dfs(2)时候 「dfs(1)的变量i的值是1」，那么在第⑤步回到dfs(1)的时候，「dfs(1)的变量i的值仍然是1」，并且从「递归处（代码⑧）」继续向下执行。

总结个“板子”

根据上面“全排列”的解法，我们可以总结出一个「回溯问题的通用思路」，下面用伪代码来描述：

res;  // 存放结果
path; // 存放当前的搜索路径
st; // 判断元素是否已经被使用

// u 表示递归处于哪一层
void dfs(u) {
    if 结束条件 {
        res.push_back(path);
        return;
    }
    for 循环 {
        // 剪枝
        // do something~~
        dfs(u + 1); // 递归，进入下一层
        // 回溯，撤销 do something~~
    }
}

下面我们就用这种方法，来批量的解决一堆回溯相关问题。

使用“板子”解决同类型题目

充分理解回溯的思路，那么就可以扩展到相同类型的题目上。

LeetCode 47. 全排列 II

（参考力扣的47题：https://leetcode-cn.com/problems/permutations-ii/）

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

思路及实现

全排列的经典扩展，给出的序列nums可能包含重复的，那么就需要考虑一个问题：「如何避免重复数字换序后，计算为新的排列方式。」

其实解决的办法很简单：「跳过重复的数字。」

举个例子：当前nums为[1,1,2]，为了便于观察我们给重复的1做上标记来进行区分，得到 ，那么就会出现 , 是同一种排列。

为了避免这种情况，以最左边的 为准，如果出现重复的就跳过去，那么当排列出 ，就不会再排列出 。

Code

实现上还有一个小细节需要注意下，给出的nums可能是乱序的，所以要先排序一下，以方便跳过相同的数字。

因为是搜索的全排列，所以排序不会对结果产生影响。

class Solution {
public:
    vector> res;
    vector path;
    vector st;

    vector> permuteUnique(vector& nums) {
        sort(nums.begin(), nums.end());
        st = vector(nums.size());
        // path = vector(nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector &nums, int u) {
        if (u == nums.size()) {
            res.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i ++ ) {
            if (!st[i]) {
                // 剪枝。如果出现重复数字，并且重复数字已经被用了，就跳过。
                if (i && nums[i - 1] == nums[i] && !st[i - 1]) continue;
                st[i] = true;
                path.push_back(nums[i]);
                dfs(nums, u + 1);
                path.pop_back();
                st[i] = false;
            }
        }
    }
};

LeetCode 39. 组合总和

（参考力扣的39题：https://leetcode-cn.com/problems/combination-sum）

给你一个 无重复元素 的整数数组 nums 和一个目标整数 target ，找出 nums 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

nums 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

思路及实现

初步看题目，发现与全排列高度相似，但又有些许不同：

1. 元素可以重复使用；
2. 结束条件不在是所有数字全部使用，而是当前路径之和为target；

那么，实现上我们要解决的一个重要难点就是：「如何让元素可以重复使用呢？」

1. 首先，为了逐步增大路径，先给 nums 排个序。
2. 因为数字可以重复使用，所以用来判重的st也就没必要使用了。
3. 最重要的是「使元素重复使用」，我们引入一个新的参数start，它表达的含义是「每次递归从start开始搜索。」这样有什么效果？举个例子就清晰了，「我们当前枚举到了i=2，那么我们把i当作参数start传到下一层，下一层又会从start开始枚举，不就重复使用i=2了嘛？」请读者将上面，加粗的描述多读几遍，细细体会一下start是如何解决本题最大难点的。
4. 「st与start的区别是什么？或者说分别在什么时候使用？」在「全排列」中，因为每个数字只能使用一次，所以我们用了st数组，把使用过的数字标记一下，这样在下一层遇到的时候，就可以跳过使用过的。例如：当前i=0，st=[1,0,0]，下一层重新从0枚举到3，当枚举到0的时候，发现st中0已经被使用过了，因此跳过了0，继续循环，得到i=1。在该问题中，因为数字可以重复使用，所以用来判重的st显然就没有存在的必要了。而为了计算重复元素，我们引入dfs()的新参数start，每次从start开始枚举就，这样每次把当前i的值传给start，那么下一层还是从当前i枚举的。但是这里引申出一个重要的问题：「下一层递归不从0开始重新枚举，不会枚举不全吗？」答案是：不会的，一个重要原因是「提前将nums从小到大，排好了序」，所以从较小的数开始枚举，一定是「一直枚举较小的数，直到较小的数也会超过target 或者 较小的数加起来等于target。」这样，对于「较小的数来说，我们已经全部放入了path，较小的数的使用个数不能再增多了（只能减少），所以也就没有枚举较小的数的必要了。」举个例子：nums = [2,3,6,7], target = 7，假设nums已经排序好，那么我们一定是一直枚举最小的数2，直到再枚举最小的数2也会超过target。那就是[2,2,2]，此时下一个2会使总和超过target，所以直接回溯，再枚举3，得到结果之一[2,2,3]。我们发现当前路径path达到[2,2,2]时，「合法路径中，能容纳的最小数2已经到上限了」，无法再增多了，而为了配合后面比他大的数，它只能慢慢减少，直到算法结束~~
5. 把当前的思路带入到“板子”中，会发现实现很简单。

Code

class Solution {
public:
    vector> res;
    vector path;

    vector> combinationSum(vector& nums, int target) {
        sort(nums.begin(), nums.end()); // 至关重要的排序
        dfs(nums, 0, target, 0);
        return res;
    }
    // dfs的参数多加一个start
    void dfs(vector& nums, int u, int target, int start) {
        // 当前路径和正好等于target时，说明找到了一个合法路径。
        if (target == 0) {
            res.push_back(path);
            return;
        }
        for (int i = start; i < nums.size(); i ++ ) {
            // 剪枝。如果超过target，直接开始回溯。
            if (target < nums[i]) return;
            // do something~~
            path.push_back(nums[i]);
            target -= nums[i]; // target减少
            // 递归。注意start处传的参数，是当前的i，所以下一层递归也会从这个i开始，
            // 这样就达到了重复使用数字的目的。
            dfs(nums, u + 1, target, i); 
            // 撤销 do something
            target += nums[i];
            path.pop_back();
        }
    }
};

LeetCode 40. 组合总和 II

（参考力扣的40题：https://leetcode-cn.com/problems/combination-sum-ii/） 给定一个候选人编号的集合 nums 和一个目标数 target ，找出 nums 中所有可以使数字和为 target 的组合。

nums 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

思路及实现

对比上一道题（组合总和），本题有两个关键点：

1. 「数字不可以重复使用」只要读者认真理解了上面一题start的含义，想必很快就能解决这个问题(就很快啊~)。在上一道题，我们为了让数字可以重复被使用，所以在start位置传了当前枚举的数字i，这样下一层枚举也会从i开始。那么显然，对于这个问题，只要把start位置的传参改成i+1就可以了。
2. 「结果不能出现重复」细心的小同学，可能已经发现了，“诶？这个问题不是在「全排列2」中解决过嘛？”没错，直接把「全排列2」中的那个剪枝拿过来就可以了（“拿来”主义狂喜~）。

Code

为了节省码字时间和文章空间，本题就不放完整代码了，正好读者可以自己试试能不能写出来。

下面写出两个关键点的实现，其余的代码和上一题“组合总和”「完全相同」。

for 循环 {
    // 剪枝。全排列2的思路：对于重复数字直接跳过就可以啦。
    if (target < nums[i]) return;
    if (i > start && nums[i - 1] == nums[i]) continue;
    // do something~~
    // 递归。数字不可以重复使用。
    dfs(nums, u + 1, target, i + 1);
    // 撤销 do something~~
}

来源：
https://mdnice.com/writing/61372f6f011243899ea639222258173a