深度学习——卷积神经网络(CNN)简介
卷积神经网络简介
文章目录
- 卷积神经网络简介
-
- 前言
- 一.如何理解卷积
-
- 1.1什么是卷积
- 1.2 为什么要卷积
- 二.神经网络的结构
- 三.卷积层
- 四.池化层
- 五.全连接层
- 六.数据训练
- 七.常见的卷积神经网络
-
- 1. LeNet
- 2 AlexNet
- 3. VGG net
- 4. ResNet
前言
卷积神经网络(Convolutional Neural Networks,简称:CNN)是深度学习当中一个非常重要的神经网络结构。它更多的是用在图像图片处理,视频处理,音频处理以及自然语言处理等等。
早在上世纪80年代左右,卷积神经网络的概念就已经被提出来了。但其真正的崛起却是在21世纪之后,21世纪之后,随着深度学习理论的不断完善,同时,由于硬件性能的爆炸式提升,算力的不断增长等因素的促进,给卷积神经网络这种算法提供了大放异彩的空间。著名的AlphaGo,手机上的人脸识别,大多数都是采用卷积神经网络。因此可以说,卷积神经网络在如今的深度学习领域,有着举足轻重的作用。
在了解卷积神经网络之前,我们务必要知道:什么是神经网络(Neural Networks),关于这个,我们已经在深度学习简介的 第二部分有所介绍。这里就不赘述了。在了解了神经网络的基础上,我们再来探究:卷积神经网络又是什么呢?当中的“卷积”这个词,又意味着什么呢?
一.如何理解卷积
1.1什么是卷积
先说点题外话,那就是这个“卷积”。刨除深度学习领域,即使是在完全没有接触深度学习之前,有相当一部分大学生,都会在本科阶段学习过一个词:卷积函数。卷积函数是说,在R1上,f(x)与g(x)是可积的,那么二者的卷积就是:
h ( x ) = ∫ − ∞ + ∞ f ( x ) g ( x − γ ) d γ = ( f ∗ g ) ( x ) h(x) = \int_{-\infty}^{+\infty}f(x)g(x-\gamma)d\gamma=(f*g)(x) h(x)=∫−∞+∞f(x)g(x−γ)dγ=(f∗g)(x)
那么这个函数的反映的是什么呢?有一种说法是:一个功能和另一个功能在时间的维度上的“叠加”作用。举一个生活当中的例子。假设我打拳,那么我打拳的动作就是f(x),我打的东西是沙袋,假设它承受我的拳可以用g(x)的表示,那么,随着我打沙袋的时间越来越差,这个作用效果最终就可以用上面这个卷积公式来表示出来。如果有朝一日,随着我打拳打的越来越好,越来越有力道,沙袋被我打漏了。那么请记住:不是我上去就把这个沙袋打漏的,而是经过我日复一日,年复一年,一拳又一拳的“叠加”,才使得沙袋最后漏掉了。
所谓的“卷积”其实就是一种“叠加”,是“日复一日”的“积累”。那么卷积神经网络,你大可以把它解释为:随着时间的推移,模型当中神经网络网络的“叠加”作用。
1.2 为什么要卷积
卷积的意义是什么呢?在深度学习当中,我为什么不能搞一个全连接的结构呢?答案其实很好解释:全连接的结构太过复杂。
卷积神经网络应用最广泛的领域就是图像识别,那,我们就拿图片来举例子。我们看下面这个例子:
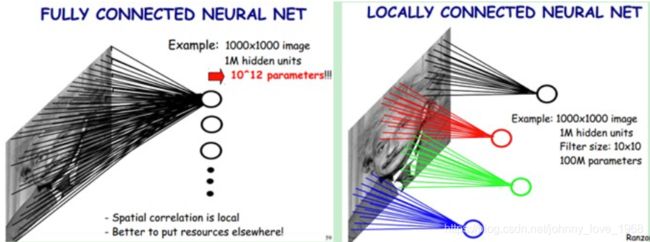
左侧,这个图是一个1000乘以1000的图片,同时,这个图片的文字说明当中说:有1M个隐藏层。如果搞全连接,也就意味着这1M个隐藏层的神经元都要和图片的每一个像素点对应,即每一个像素点,都要把所有的隐藏层都给过一遍,意味着需要有:1000*1000*1M = 10^12个连接,同时也意味着,有10^12个权值,这就会导致模型极其复杂。
但是,如果我搞卷积神经网络,神经网络当中需要“过滤器”(这个可以先看看第三部分),假设这个过滤器是10乘10的,在具体的链接当中,我们只需将这个“过滤器”和图片进行全连接,那么就是10*10*(1000*1000) = 10^8,比起10的十二次幂,已经少了很多了。
但是,如果每一个“过滤器”所表示的图片都很简单,都是一个很简单的特征呢?也就是过滤器当中的元素,0居多,1占少数,那么这100个像素当中,其实真正能起作用的并不多。那么,如此一来,需要的全连接次数就会更加大大的减少。那,如果我想识别的图片很复杂呢?那我就多搞一些不同的,同样简单的过滤器嘛。事实证明,这样做的效果,也不错,而且比十的八次幂要小很多。
说道这里,卷积神经网络的一条思路就出来了:通过一个个很简单的“过滤器”,来不断的筛选出和“过滤器”相近的特征,通过不断的训练,把这些特征进行组合,就能识别出原图片是什么个东西了。
二.神经网络的结构
既然神经网络要“叠加”,要“积累”,那么怎么一个积累法呢?答案就是:在神经网络当中引入卷积层的概念。如下所示,我们以神经网络当中的AlexNet为例,注意红框部分。当中是卷积层与池化层的交替。在卷积神经网络当中,卷积层和池化层可以有很多层,没有具体的数量限制。
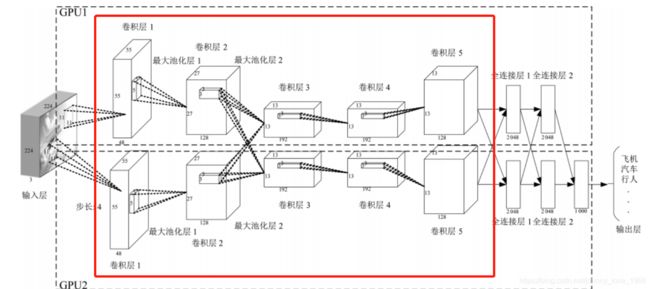
同时注意,卷积神经网络当中,很多时候也会经过一些调整,比如说,在输入层和卷积层之间加入若干其他的Hidden Layer,如:用于“加权”的ReLU等等。
三.卷积层
顾名思义,卷积层,就是用来做“叠加”的,具体怎么一个叠加方式呢?(即:如何做卷积,同时,忘记之前的那个积分运算)
我们以图像识别为例,我们知道,图片,都是由一个个像素组成的,我们可以用0表示白,1表示黑,那么可以由各种0,1组成一张黑白照片。同时呢,我们准备一个“过滤器”,在一些资料当中,这个被称为“卷积核”,是做卷积运算的一个关键“组件”,本质上,它是一个矩阵,假设,这个矩阵是:
( 1 0 1 0 1 0 1 0 1 ) \begin{pmatrix} 1& 0 &1\\0 &1 &0\\1& 0& 1 \end{pmatrix} ⎝⎛101010101⎠⎞
然后,我们就可以按照下方这个动图所演示的这样,每一块都做一下矩阵的乘法运算。这样就得到了一组卷积特征值,这些个卷积特征值,又会组成一个新的矩阵。
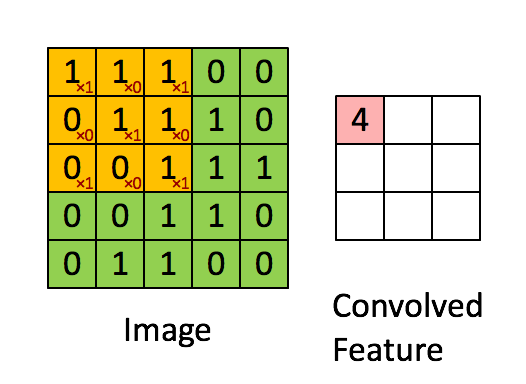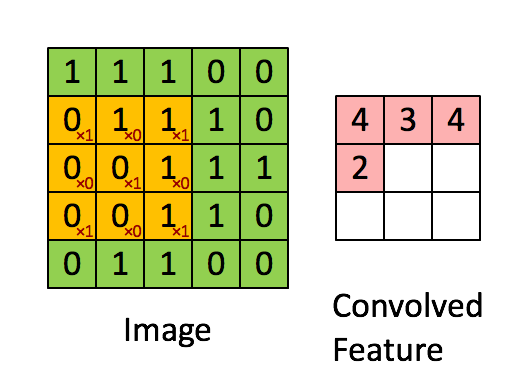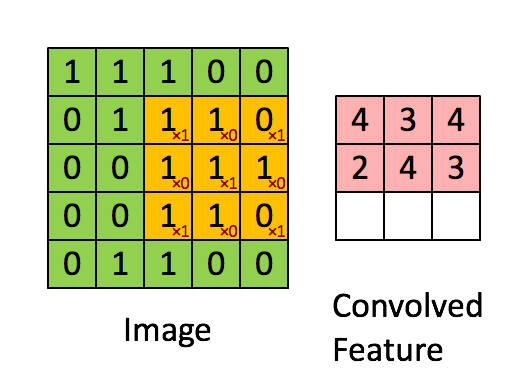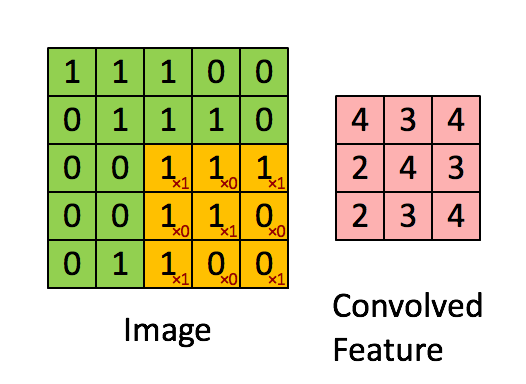
那么,如何理解这个“过滤器”呢?其实,过滤器代表了一种图像模式,如果某个图像块与此卷积核卷积出的值大,则认为此图像块十分接近于此卷积核。在现实当中,一个图片往往很复杂,因此需要多个“过滤器”的加持,每个过滤器彼此都代表了不同的图像模式,这样不停的做这种矩阵乘法运算,就会得到若干个卷积特征。那么得到卷积之后,我们该如何选择呢?这个时候就需要池化层了。
四.池化层
英文名:Pooling,所谓的“池化”,其实是指特征值筛选。比如说,没经过一个“过滤器”的计算,整个图片都会形成一个卷积特征矩阵,我挑选当中元素值最大的(其实就相当于把和卷积核最像的那部分给提取出来了)。这个图片在经历所有的“过滤器”运算后,我就可以把这当中所有的最大值都给筛选出来,这样一来,就会组成一个新的图形矩阵。在卷积神经网络当中,这是池化的方法之一:max-pooling。
在经过这样的运算之后,我们发现,原来图片的样本,在经过池化之后,明显缩小了。如下图所示:原本的图片是10*10的,但是经过池化之后,变成了2*2
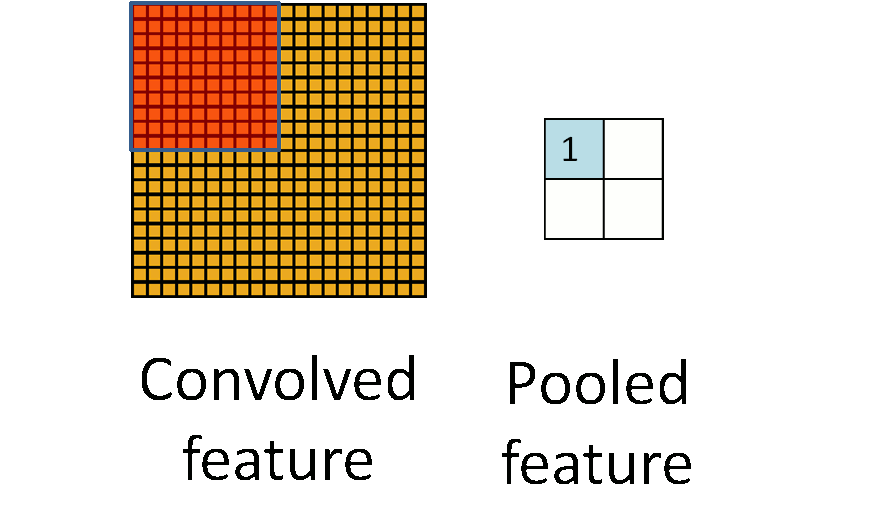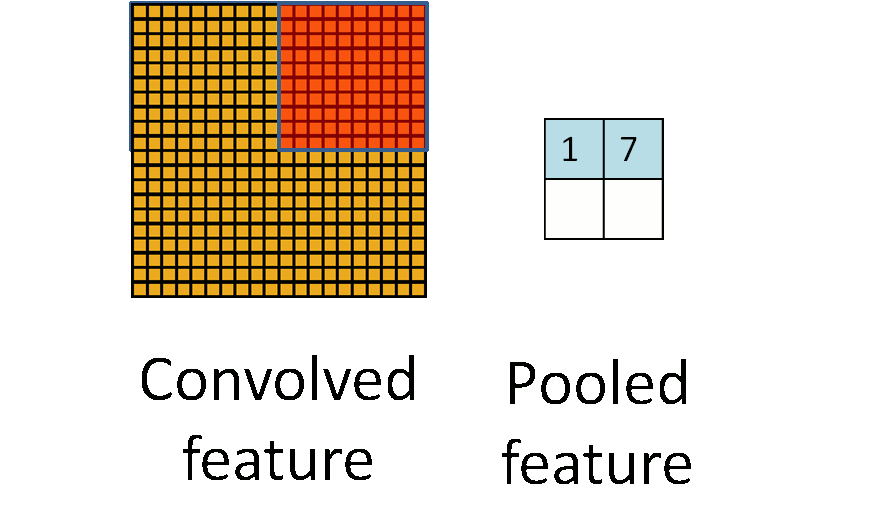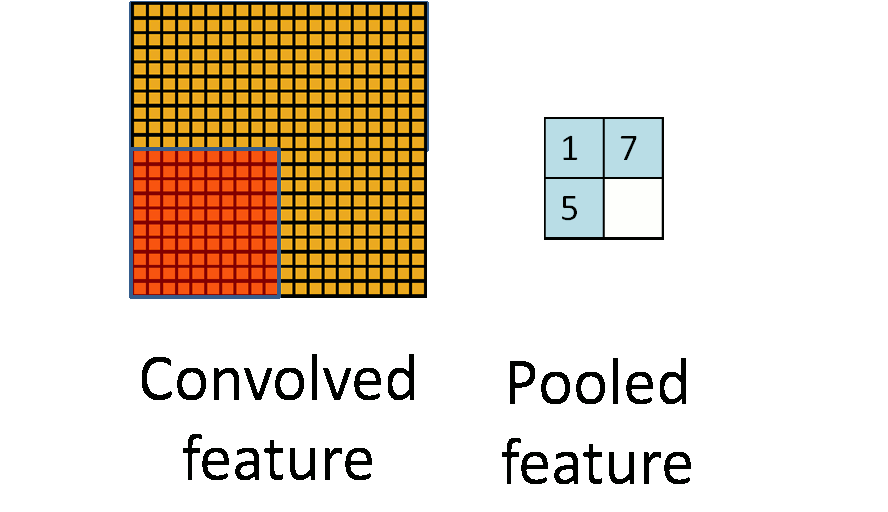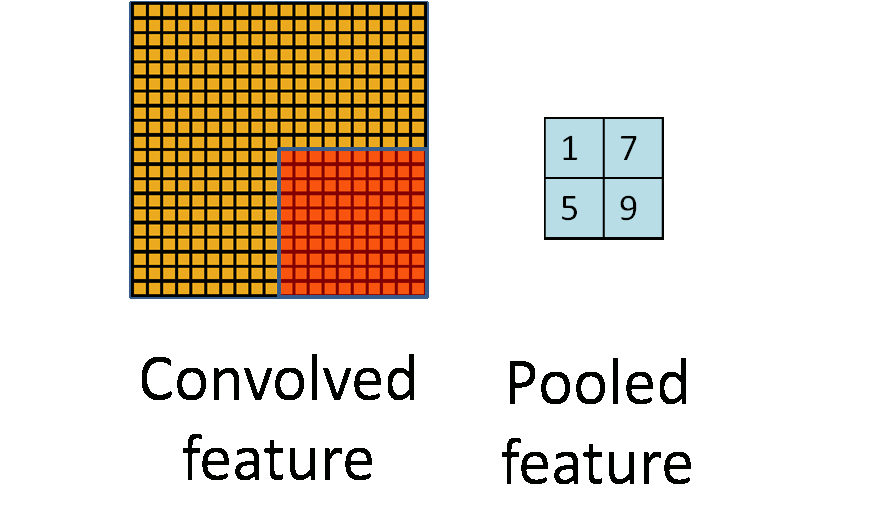
某些方面讲,这是一种“降维”,也是防止过拟合的一种手段。不过,在现实当中,图片往往比起“过滤器”,要大的多得多。因此,即使经过一次池化过后,往往也还是一个很大的样本。虽然变小了,但是筛选出来的,却和各个“过滤器”都比较相近,通过这些个“过滤器”,大体就可以拼凑出,这个图片到底是个啥。随着训练次数的增多,也就越来越接近原图片。
在卷积神经网络当中,有若干种池化方法,比如说,矩阵运算之后,所有的都取平均值,这个叫:average-pooling。
五.全连接层
在经过池化(特征提取)之后,原有的图片被降维了,经过一次次的卷积核特征提取,最后得出来的,都是“精华”。既然,维度被大大缩小了,而且还都是精华数据,那么这个时候,全连接就应该使用上了。
六.数据训练
卷积神经网络也是深度学习的一种。在深度学习当中,我们有前向传播和后向传播,卷积神经网络也不例外,这部分的原理,参考这个文章:深度学习——反向传播
七.常见的卷积神经网络
1. LeNet
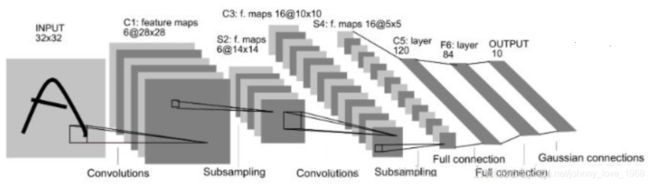
LeNet的提出时间是比较早的,属于早期的卷积神经网络,最初的目的是为了解决手写文字的识别问题。LeNet结构简单,但是麻雀虽小,五脏俱全。现在神经网络当中的卷积层,池化层,全连接层等,已经在LeNet当中提出来了。
LeNet大致上有七层:
- 输入部分,输入的的是一张32*32图片,上面为用户手写的数字;
- C1 卷积层,卷积层当中所应用的卷积核,其大小为5*5,深度为6,没有padding, 卷积核扫描整个图片的步长(stride)为1,经过一轮卷积之后,C1输出的尺寸是28*28,深度是6.
- S2 是池化层,你可以用Max Pooling, 也可以使用Average Pooling;
- C3 是新的一个卷积层,卷积核大小仍然是为55,没有padding, stride大小为1,但深度为16,经过C3层的卷积,最后会形成一个1010的feature maps,深度为16.
- S4 是新的一个池化层,过滤器大小为22,stride=2,因此输出的是一张55的feature maps,深度为16.
- C5 是全连接层,卷积核大小为5*5,最后也一定会得到一个shape = [5,5,16]的向量。
- F6也是一个全连接层输出84个节点
- 输出层也是全连接层,输出10个节点。
2 AlexNet
也就是我们之前用来举例的那张图

如果说LeNet是奠定了卷积神经网络的一个基础,那么AlexNet就是飞跃了一大步。现在神经网络当中应用的许多技术,在AlexNet当中都有所体现,比如说:
- 使用了ReLU函数,避免的梯度的消失问题;
- 正则化(如Batch Norm)在AlexNet当中大量使用,加快了运算效率
- 引入Drop Out技术,极大的避免的过拟合
从结构上看,AlexNet也有独有的特点:
- 我们知道,综合来看,GPU的运行速度要远快于CPU,于是AlexNet当中采用了双CPU运行;
- 卷积层,池化层的交替使用,全连接层的应用被完美的继承了下来。
3. VGG net
这个神经网络探索了卷积神经网络的深度和其性能之间的关系,通过反复的堆叠33的小型卷积核和22的采用了Max Pooling的池化层,成功的构建了16~19层深的卷积神经网络。这个神经网络的结构如下:
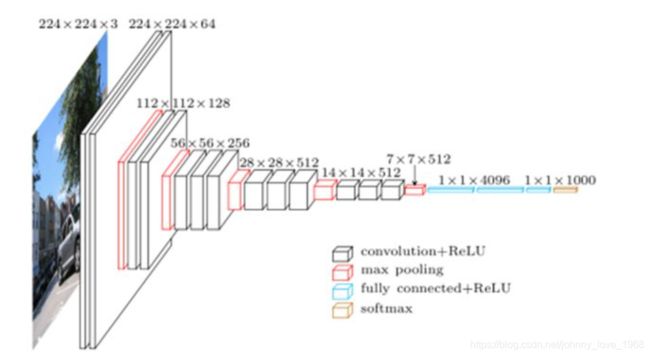
4. ResNet
ResNet所使用的方法真的很大胆。我们知道,在神经网络当中,随着迭代次数越来越多,当我们大量使用Sigmoid,或者tanh函数的时候,由于两端的梯度几乎接近为0,这就使得梯度下降变得失效。对此,很多人又提出了momentem,ReLu等方法
但是在ResNet当中没有这样,它采用的方法是:输入数据不会输入到所在的Layer,而是直接输入到下一个Layer当中,如图所示:
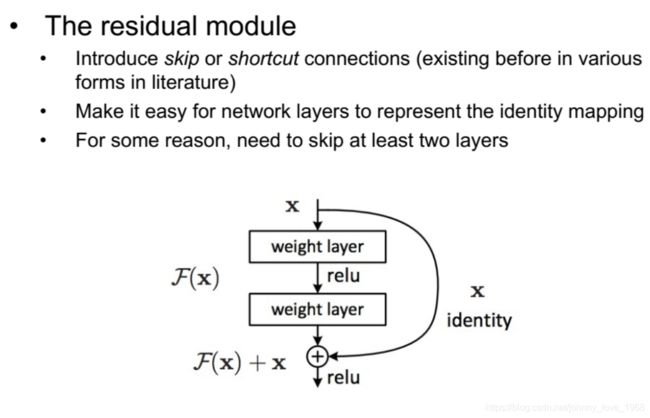
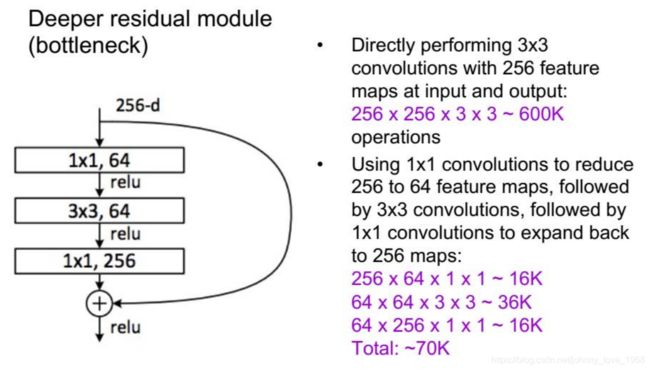
在实现上,一般采用Residual Module,如下所示: