【雷达目标检测】恒定阈值法和恒虚警(CFAR)法及代码实现

实验原理

1.1 目标检测概念

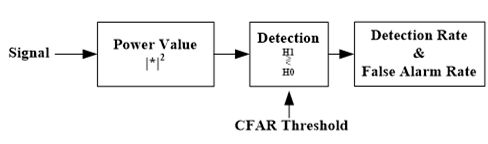
在接收到回波信号后，我们需要对信号进行处理，以区分目标与噪声、杂波和干扰。

目标检测方法的核心是阈值法。
如果雷达回波大于阈值，则显示检测到目标，否则视为噪声。

经典的检测问题可以建模为一个二元假设问题。
$$H_0:z=n$$ $$H_1:z=1+n$$
其中$n$是满足$N(0,1)$的加性高斯白噪声。
所以，每次进行实验时，可能会发生以下四种情况之一：

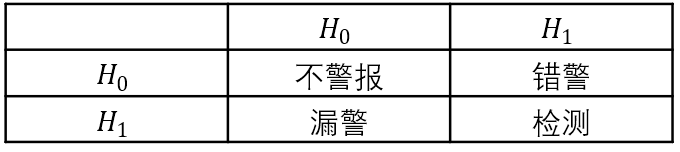第一行表示预测结果，第一列表示实际情况。具体来说，当H1为真，我们选择H1时，信号被称为被检测到。当H0为真时，我们选择H1，这就是假警，错误检测。

雷达回波总是含有噪声，噪声会引起错警和漏检，但同时降低虚警概率与提高检测概率之间存在矛盾，因此需要精心设计阈值。

1.2 恒定阈值

对于单个数据样本的最简单情况，虚警概率为$P_{FA}=e^{-T}$，其中T是检测阈值。So,固定虚警率，阈值为$$T=-ln{P}_{FA}$$。

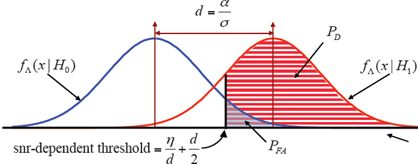
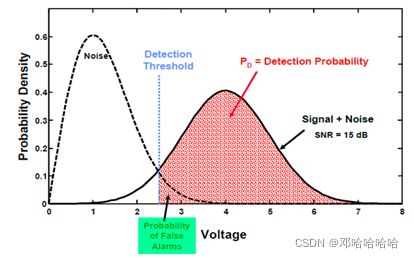
对于unnormalized data sample 和 绝对律检测器，阈值是$$T=\sqrt{-{\sigma }^{2}ln{P}_{FA}},$$其中，其中${\sigma }^2$是干扰的总噪声功率。虚警概率为$P_{FA}=e^{-T/{\sigma }^2}$。检测过程如下图所示。

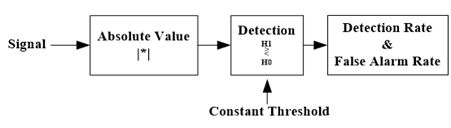
请注意，阈值T与噪声功率成正比。当雷达接收机输出的干扰发生变化时，实际$P_{FA}$将剧变。对于雷达系统来说，当干扰增加时，假警报的数量也会增加。因此，应调整固定阈值以保持所需的$P_{FA}$。

1.3 恒虚警率（CFAR）检测

根据以上内容，我们知道应该调整阈值以保持所需的$P_{FA}$。我们将在这里介绍基本的单元平均CFAR（CA CFAR）方案。
CA CAFR使用当前待检测数据周围一定范围的单元格的平均值来确定被测单元格的阈值，如下图所示。

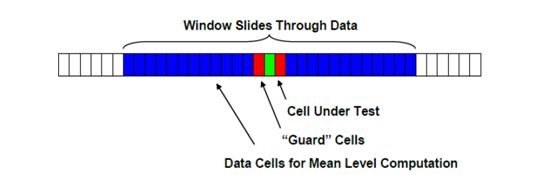Guard cells: 保护间隔
Window：做CA-CFAR的数据长度

使用平方律检测器时，估计的阈值为

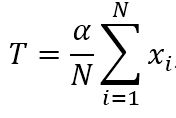
其中x是平方律检测器的输出，$$\alpha =N(P_{FA}^{-1/N}-1),$$N是相邻单元的数量，即蓝色单元，$P_{FA}$是虚警概率。检测过程如下图所示。

实验内容

2.1 恒定阈值法

实验参数：
SNR：0-20dB
误警率：0.001

2.1.1 目标检测模拟

利用1.2所述公式$T=\sqrt{-{\sigma }^{2}ln{P}_{FA}},$算得阈值。
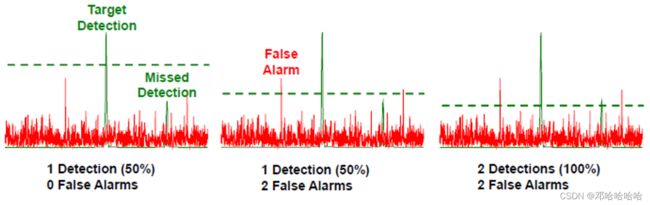
我们绘制了噪声、噪声+信号的pdf和时域波形，虚线为阈值。
1） SNR = 0dB 时：
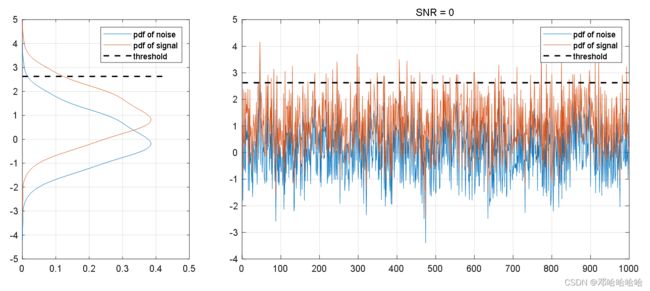2) SNR = 10dB 时：

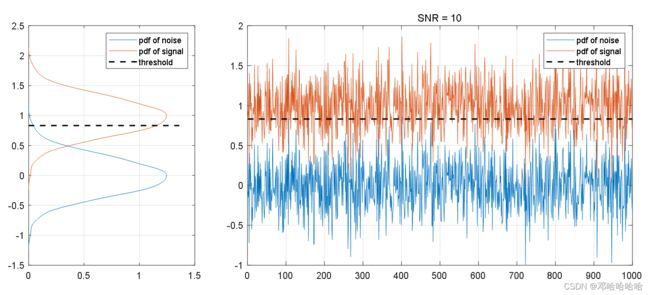
2.1.2 检测概率

重复实验次数：100
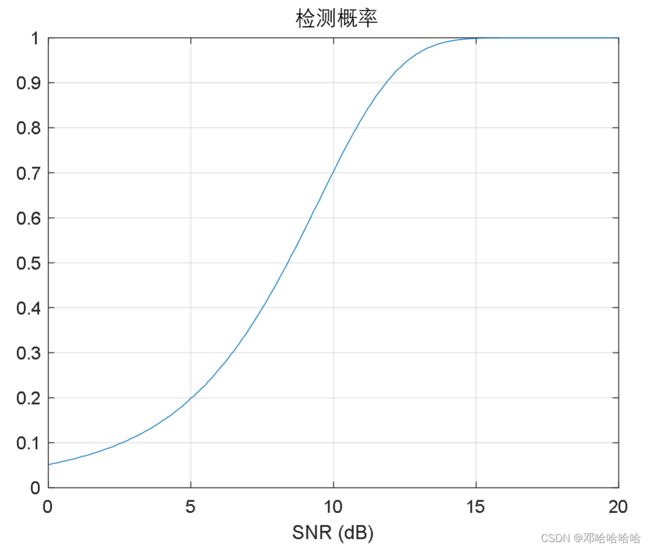检测概率$P_D$随着信噪比的增加而增加。
改变$P_{FA}$，我们可以看到$P_D$会随着$P_{FA}$的减小而减小。

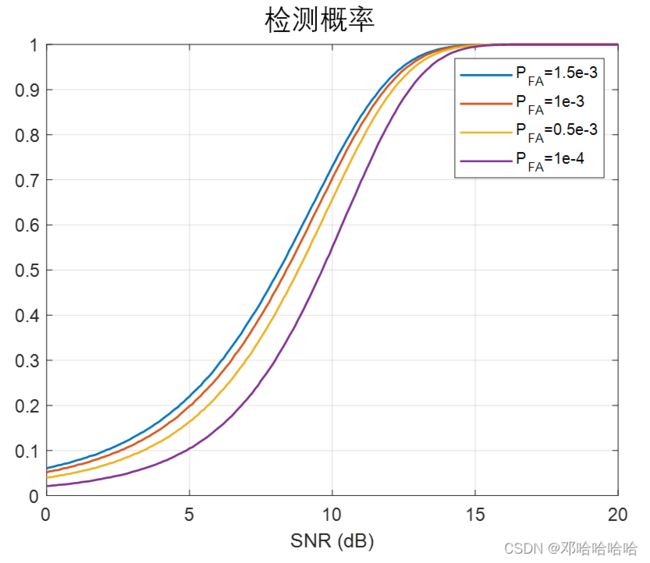
2.2 CA-CFAR恒虚警

参数设置：
窗长（单边）：10
保护间隔：1
错警率：0.001
重复实验次数：1000
SNR：0-20dB

2.2.1 目标检测

我们演示了在SNR=10dB和SNR=15dB的情况下的检测过程。黑色实线表示恒虚警阈值，红色实线表示恒定阈值，橙色实线表示噪声，蓝色实线表示信号加噪声。

1. SNR = 10dB
   
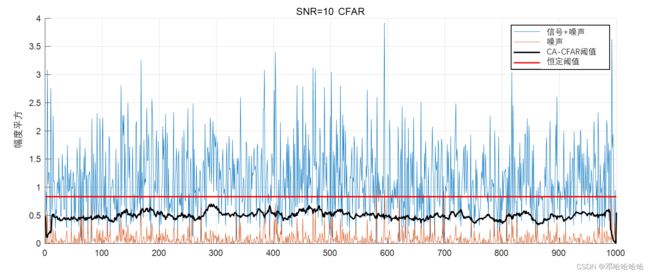
2. SNR = 15dB
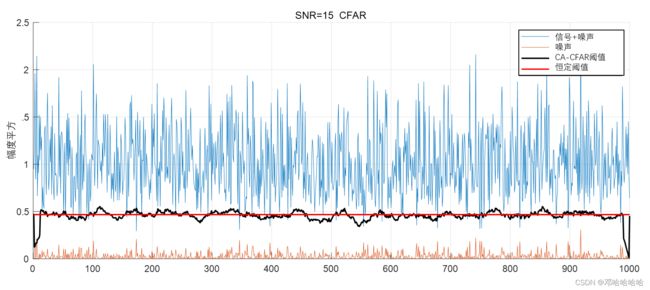   我们可以看到，当信噪比相对较小时，即10dB，恒定阈值远高于恒虚警阈值，因此恒虚警的检测率更好。
   当信噪比相对较大时，即15dB，恒虚警阈值相当于恒定阈值，因此两种方案可能具有相同的检测率。

2.2.2 检测概率和错警率

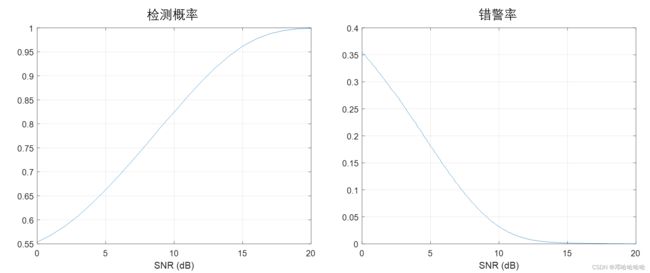可以看出，检测概率随信噪比的增加而增加，而虚警概率随信噪比的增加而降低。

2.2.3 其他参数

窗口的长度会影响性能，我们对此进行了模拟。
M表示窗长。
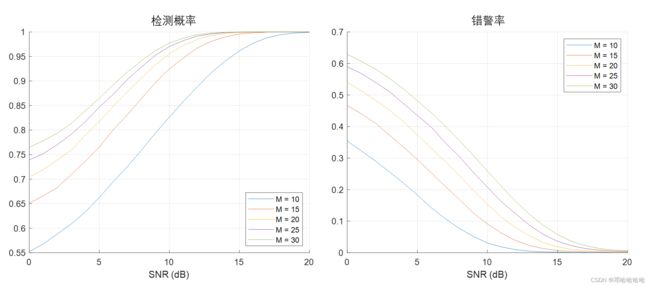M增大，检测率和错检率都增大。

2.2.4 CA-CFAR和恒定阈值比较

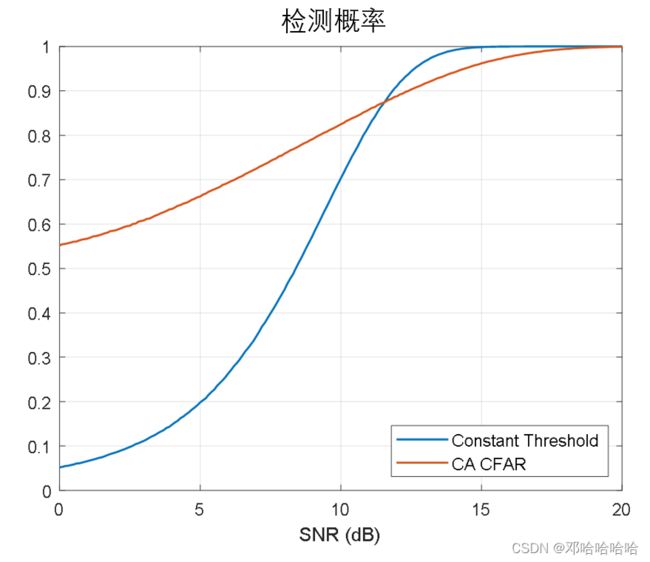
从图中可以看出，当信噪比相对较小时，CA-CFAR方法的$$P_D$较高，而当信噪比相对较大时，恒定阈值方法较好。当信噪比大于18dB时，两种方法的检测概率都达到饱和。
例如，如果我们想要得到指定的$P_D$=0.8，我们需要要求恒定阈值的信噪比比比CA-CFAR方案高出约4.5dB。
正如我们在恒虚警检测的部分仿真中所述，当信噪比较小时，由于恒虚警方案可以充分利用干扰，因此我们可以获得更好的阈值。当信噪比较大时，这两种方案具有等效阈值，且信号和噪声具有很强的可分离性。

2.3 MATLAB实现

clc;clear;close all
% 参数
signal = 1;
SNR = 10:0.1:20;
Pfa = 1e-3;
N = 1000;       % 信号长度
Q = 1000;       % 重复实验次数

Pd = zeros(2,length(SNR));       % 检测概率
Pf = zeros(2,length(SNR));       % 错警率
T_a = zeros(2,length(SNR));      % 阈值

for r = 1:length(SNR) 
    snr = SNR(r);
    for q = 1:Q
        sigma2 = signal/(10^(snr/10));  % 噪声方差
        x = ones(1,N)*sqrt(signal);     % 信号
        noise = sqrt(sigma2)*randn(1,N); % 噪声
        x = x + noise;       % 信号+噪声
        % [fn,xn] = ksdensity(noise);   % 噪声pdf
        % [fs,xs] = ksdensity(x);       % 噪声+信号的pdf
        % ============== 恒定阈值 =================
        T1 = sqrt(-1*sigma2*log2(Pfa)/log2(exp(1)));
        T_a(1,r) = T_a(1,r)+T1;
        t = 1:N;
        Pd(1,r) = Pd(1,r) + sum(abs(x)>T1);
        Pf(1,r) = Pf(1,r) + sum(abs(noise)>T1);
        
        % =================== CA CFAR ===================
        M = 10;   % length of window (single side)
        g = 1;    % length of guard cells(single side)
        % 平方律
        y = abs(x).^2;
        n = abs(noise).^2;
        k = Pfa^(-1/2/M)-1;
        T2 = zeros(1,N);
        for i = 1:N
            if i == 1 
                cell_right = 1/M*sum(y(i+g:i+g+2*M));
                Z = cell_right/2;
            end
            if i>1 && i < M+g+1
                cell_right = 1/2/M*sum(y(i+g:i+g+M-i-1));
                cell_left =  1/M*sum(y(1:i-g));
                Z = (cell_left+cell_right)/2;
            end
            if M+g+1<=i && i<= N-M-g
                cell_left = 1/M*sum(y(i-g-M:i-g));
                cell_right = 1/M*sum(y(i+g:i+g+M));
                Z = (cell_left+cell_right)/2;
            end
            if i> N-M-g && i<N
                cell_left = 1/M*sum(y(i-g-M+i+1:i-g));
                cell_right = 1/M*sum(y(i+g:N));
                Z = (cell_left+cell_right)/2;
            end
            if i == N
                cell_left = 1/M*sum(y(i-g-M*2:i-g));
                Z = cell_left/2;
            end
            T = k*Z;
            T2(i) = T;
            
            if y(i) >= T2(i)
                Pd(2,r) = Pd(2,r)+1;
            end
            if n(i) >= T2(i)
                Pf(2,r) = Pf(2,r)+1;
            end
            
        end
    end
end

% 取平均
Pd(1,:) = Pd(1,:)/Q/N;
Pf(1,:) = Pf(1,:)/Q/N;
Pd(2,:) = Pd(2,:)/Q/N;
Pf(2,:) = Pf(2,:)/Q/N;
T_a = T_a/Q;
 
figure;
plot(SNR,Pd(1,:),'LineWidth',1.2);
title('Probability of Detection');
xlabel('SNR (dB)');
grid on
hold on
plot(SNR,Pd(2,:),'LineWidth',1.2);
legend('恒定阈值','CA CFAR');

参考文献

《雷达信号处理》