线性表知识掌握了么?
前言:
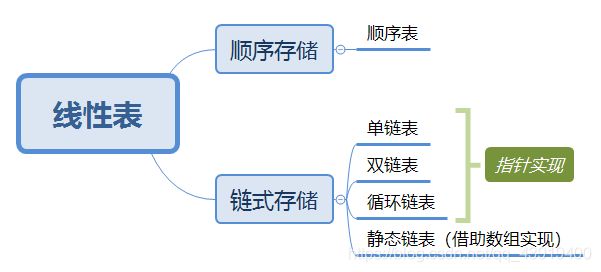
首先我们给出本文的知识框架:
照着上面的思维导图问问自己几个问题:链表的基本操作会定义吗?删除插入的指针放在哪?循环链表的插入删除呢?如果还有一些模糊,那么和我一起往下看吧。
一、线性表的基本操作
我们在顺序表以及链表的学习其实就是去学会如何实现下面的基本操作,所以下面列举几个基本操作(这些方法在java等高级语言里面可以直接调用,这里我们可以感受一下底层的快乐,即使现在看起来很简单,但是结合起来就需要花费一定的功夫了)。
主要操作:
InitList(&L):初始化表。构造一个空的线性表。
Length(L):求表长。返回线性表L的长度,即L中数据元素的个数。
LocateElem(L,e):按值查找操作。在表L中查找具有给定关键字值的元素。
GetElem(L,i):按位查找操作。获取表L中第i个位置的元素的值。
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值。
PrintList(L):输出操作。按前后顺序输出线性表L的所有元素值。
Empty(L):判空操作。若L为空表,则返回true,否则返回false。
DestroyList(&L):销毁操作。销毁线性表,并释放线性表L所占用的内存空间。
以上的基本操作,简单的逻辑就是从创建初始化,进行增删查改等操作之后销毁这一生命过程,那么我们先来看看顺序表示如何去实现。
接下来用这几个字符来代替1,0,-2几个数字
#define OK 1
#define ERROR 0
#define OVERFLOW -2
二、顺序表
定义:用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻(你可以理解为高级语言里面的数组的特性)。从这句话中我们就可以知道顺序表表中的元素的逻辑顺序和物理顺序相同。如果我们用L表示第一个元素所在的位置,并且每个元素所占用的空间为4,那么第n个元素的物理地址就是L+(n-1)*4。
在我们开始定义一系列的操作之前,首先就是定义结构体来将我们顺序表里面需要表达的东西定义一个结构(例如我们需要知道表L的指针是什么,怎么指向它,知道表里面当前元素的个数,当然你还可以定义其它的,这里就简单的定义顺序表的元素和长度)。
//静态分配,我们定义顺序表结构体的时候直接给数组赋予固定的大小,如下直接data[MaxSize]
#define MaxSize 50
typedef struct {
ElemType elem[MaxSize];//顺序表的元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
//动态分配,我们在定义结构体的时候不固定给出数组大小,而是通过(C++)new EmlemType[Size]来动态的分配大小(所谓动态的分配就是程序运行时动态从堆中分配空间出来)。
#define IniteSize 100 //表长度的初始定义
typedef struct {
ElemType *elem; //指示动态分配内存的指针
int MaxSize,length; //数组的最大容量和当前个数
}SqList; //动态分配数组顺序表的类型定义1、初始化
这里初始化我们就是去定义一个空的顺序表,也就是说做两件事情:(1)为表中的元素初始化空间;(2)初始化表长length,当然,动态分配因为存在指针进来,所以我们需要进行if-else的判断让我们的程序代码拥有健壮性。
typedef int Status; //Status 是函数返回值类型,其值是函数结果状态代码。
Status InitList(SqList &L)
{//构造一个空的顺序表L
L.elem = new ElemType[MAXSIZE]; //为顺序表分配一个大小为MAXSIZE的数组空间
if(!L.elem) exit(OVERFLOW) //存储分配失败退出
L.length = 0; //空表的长度为0
return OK;
}我们就为顺序表分配了空间,判断是否分配失败,然后为表长赋初始值而已。
2、取值
我们可以思考如果要从顺序表中取出一个值(直接a[i]不就行了嘛,但是考虑到程序的可复用性,这里采用严蔚敏老师书中的写法),那么函数的参数有三个:该顺序表的指针,位置序号i,以及用来存储i号位置的变量。所以代码就有:
Status GetElem(SqList L,int i,ElemType &e)
{
if (i<1||i>L.length) return ERROR;
e = L.elem[i-1]; //第i个元素其实就是elem[i-1]
return OK;
}我们当然也可以让返回值为具体的数据类型,然后做出判断之后如果成功直接返回elem[i-1]就好。
3、查找
这里按值查找,那么我们肯定是直接进行for循环,如果找到的话可以返回位序,若失败返回0。
int LocateElem(SqList L,ElemType e)
{
for(int i = 0;i如果你看过《刷算法题?首先要学会基础的算法分析!(递归算法的数学分析和非递归算法的数学分析demo)》我的这篇博客的话,会很简单的看出来下面是对上面算法做平均时间复杂度的分析,因为它的最好情况仅需比较一次,也就是时间复杂度为O(1);最坏的情况就是比较n次(查找的元素在表尾或者不存在),也就是时间复杂度为O(n)。而下面(字比较丑别建议啊,哈哈哈)就是对平均情况的分析:
之后对删除和插入的时间复杂度分析我们就直接给出,不在啰嗦了呀。
4、插入
我们可以立马想到,在顺序表中插入,例如有10个元素,而我想在第5个位置插入,那么从当前位置的第五个一直到最后一个元素也就是第10个元素都需要向后移动一位,腾出位置嘛。所以我们可以想到函数的参数列表应该要有想要插入的元素值和插入的位置,以及顺序表的指针。而返回值就可以返回状态,即ERROR失败,return OK则成功。
Status ListInsert(SqList &L,int i,ElemType e)
{//肯定需要判断i的范围
if((i<1)||(i>L.length+1))//这里的i不是数组的下标,而是指第几个位置
return ERROR;
if(L.length==MAXSIZE) return ERROR;//判断一下存储空间是否已经满了
return ERROR;
for(j=L.length-1;j>=i-1;j--) {//先将这个位置及其以后的元素都向后移动(这里向后循环就不会改变先前的值),再插入进来
L.elem[j+1] = L.elem[j];
}
L.elem[i-1] = e;
++L.length;
return OK;
}我们进行一个小小的算法分析(一看就知道基本操作为元素的赋值,也就是移动的操作):
最好情况:直接在表尾插入就不需要移动了,所以时间复杂度为O(1)。
最坏情况:在表首插入,那么往后的每一个元素都要向后移动一位,所以时间复杂度为O(n)。
平均情况:我们依旧假设pi=1/(n+1),也就是说插入的每一个位置都是相等的(这里不要觉得为啥是n+1呀,因为尾部也有一个位置可以插入嘛)。而在i处插入元素有向后移动为n-i+1次。所以直接求和符号就有:
所以时间复杂度为O(n)。
5、删除
试想如果你想在顺序表中删除元素,你会怎么做,可能就是找到对应的位序,然后删除对吧。所以这里函数的参数列表需要有位序i和顺序表的引用(这里和插入肯定相反,所以也有元素的移动,向前移动),那么有:
Status ListDelete(LqList &L,int i)
{
if((i<1)||i>L.length) return ERROR;//这里在说明一下,i不是指数组下标,而是位序,所以多了1很正常哦
for(j=i;j时间复杂度分析(基本操作也是移动):
最好情况:删除的是表尾元素,所以时间复杂度为O(1);
最坏情况:删除的是表首元素,所以时间复杂度为O(n);
平均情况,我们设pi也是一样的,就是说删除每个元素的概率是相等的,所以pi=1/n。而删除第i个元素移动的次数有n-i,所以公式有D=(n-1)/2。
所以时间复杂度为O(n),接下来我们来学习线性表的基础。
三、单链表
单链表的重要性不需要多说,让我们来看看它的定义:
线性表的链式存储又称单链表,它是指一组任意的存储单元来存储线性表中的数据元素。为了建立数据元素之间的线性关系,对每个链表结点,除存放元素自身的信息外,还需要存放一个指向其后续的指针。其中data为数据域,存放数据元素;next为指针域,存放后续结点的地址。(这里不要混淆结点和节点哦,这里的结点可以理解为一团东西:两部分组成,一个数据数,一个指针域。而另一个节点,和我们这没有关系)。
这里我们需要注意的是,我们总是会定义拥有头结点的单链表,这个头结点的定义让我们对链表的第一个节点操作更加的方便(例如头插法创建的时候),而且也便于空表和非空表的处理(你想啊,现在大家都至少有一个节点,判空不管你是非空还是存在都只需要L->next==null就可以判断,如果没有头结点,那么判空就L==null)。
那在我们进行如上面顺序表一样的操作之前(初始化、取值、查找、插入、删除、创建),先和上一样定义存储结构:
typedef struct LNode
{
ElemType data; //结点的数据域
struct LNode *next; //结点的指针域
}LNode,*LinkList; //LinkList为执行结构体LNode的指针类型
这里为了提高程序的可读性所以才定义了LNode和LinkList,我们用LinkList L定义单链表,强调定义的是某个单链表的头指针;用LNode*定义执行单链表中任意结点的指针变量1、单链表的初始化
初始化,那么肯定就是构造一个空表。
Status InitList(LinkList &L)
{//构造一个空的单链表L
L = new LNode; //生成新结点作为头结点,用头指针L指向头结点
L->next = NULL; //头结点的指针域置空
return OK;
}这里我们new了一个新结点,然后让指针域指向空,这里依旧可以记住LinkList可以作为链表的头结点,代表链表;而LNode*就可以作为定义的指针标量到处行走,下面的操作也是这样定义的。
2、取值
从取值就可以体现出顺序表和单链表很大的区别,我们在顺序表中取值时间复杂度为O(1),因为是顺序存储,我们直接可以取到,而在单链表中就不行。我们可以思考一下函数的参数,我们可以是两个参数,一个链表的指针L,一个是序号int i,这样的话函数需要有返回值int。这里我们参考严蔚敏老师书本上的使用三个参数,将取到的值保存在e中即可,算法描述如下:
Status GetElem(LinkList L,int i,ElemType &e)
{
//在带头结点的单链表L中根据序号i获取元素的值,用e返回L中第i个数据元素的值
p=L->next;j=1;
while(p&jnext;
++j;
}
if(!p||j>i) return ERROR;
e=p->data;
return OK;
} 上面的代码没有上面难度,但一定要做好错误处理。我们思考一下时间复杂度,直接就知道是O(n)(这里不再做分析,上面也分析过了,对于这种非递归的算法,分析的套路都是一样的,如果有最好最坏可以讨论一下,相对来说平均时间复杂度是比较难的。这里我们可以如上分析的一样,假设取到每个元素的概率相等也就是1/p,那么求和表达式不就是1+2+...+(n-1)吗?所以时间复杂度当然是O(n),下面不在赘述)。
3、查找
这个小部分和上面是完全一样的,上面是按序号去查找,而这里只是换成了按值查找而已。我们简单思考一下,将返回值变成LNode结点类型就好,代码内部script不同的是仅仅是while循环里面的判断语句修改了。如下:
LNode *LocateElem(LinkList L,ElemType e)
{
p=L->next;
while(p&&p->data!=e)
p=p->next;
return p;
}那么我们老规矩来看看时间复杂度,这里的,不用看就知道其平均时间复杂度和上一样是O(n)了。这里点非常的重要,因为在各种应试题目中总是会忽略LocateElem的时间复杂度,而觉得在某个元素前或者后插入元素时间复杂度为O(1),切记!
4、插入
看到这里的时候,如果你旁边有一只笔就更好了,因为你可以在纸上清晰的画出插入的线条。这里我总是有一个习惯:先让要插入的元素去指向后面个元素,然后让前面那个元素在指向这个新插入的元素。千万别绕,这不难,只要你画个图就能够明白。上面的图片我也是这个步骤,你问我为什么,如果你仔细观察就会发现,如果改变顺序,先(2),那么p->next其实已经发生改变成为x了,而再进行(1)操作,就相当于x->next = x;这不是闹着玩吗???
这里其实可以养成这样的习惯,在双向链表和循环双链表的插入部分都是很有用的。不过对于单链表我有一个巧记的方法,就是如果我想要征服一个地方(假设这个地方有一个老大),那么我要先收拾它的手下(这里对应先指向后面的那个结点),之后老大就会来找我solo(之类表示前面的结点指向我),然后我就成功征服进入这里了(conquer)。
写代码:要插入一个新节点,那么我们首先肯定要知道将要插入的位置,所以这里函数有参数int,然后要插入的值,以及要插入的链表L。在代码内部我们肯定也是先按序号查找,所以这里有O(n)的时间复杂度,找到之后就开始插入,但是肯定是要借助一个辅助指针的,这就定义为p吧,也就是如上图中显示的一样。
Status ListInsert(LinkList &L,int i,ElemType e)
{
p=L;j=0;
while(p&&(j-1))
{
p=p->next;++j
}
if(!p||j>i-1) return ERROR;
s=new LNode;
s->data=e;
s->next=p->next;//对应插入的第一步
p->next=s;//对应插入的第二步
return OK;
}
老规矩,最后 也看看时间复杂度,我们发现其实按值查找时间复杂度就是O(n),后面插入也就几行代码,所以时间复杂就是O(n)。
5、删除
大家可以先忽略上面图片中的文字,自己思考一下,如果你要删掉一个元素怎么操作呢,在顺序表中我们会直接向前移动n个位置。在链表里面显然要简单得多,只需要将指针的位置移动一下就好。
对比上面的插入操作,你会发现我们用到了一个辅助指针p,那是因为我们只需要定位到插入的前一个位置即可;而这里除了需要定位到前一个位置(使用辅助指针p以外),还需要一个指针q执行被删除的元素,这样我们好释放这个资源,所以q指针的作用就是这么卑微。
Status ListDelete(LinkList &L,int i)
{
p=L;j=0;
while((p->next)&&(jnext,因为合法的删除位置只有n个,而对于插入来说,合法的插入位置有n+1个,所以判断条件不同
{
p=p->next;++j;
}
if(!(p->next)||(j>i-1)) return ERROR;
q=p->next;
p->next=q->next;
delete q;
return OK;
}
细心的的你肯定会发现插入和删除里面while循环的判断条件竟然不相同!!!虽然在上面代码注释中说了一遍,这里再次强调一遍,p->next和p作为判断条件是不一样的。合法的删除位置比合法的插入位置少一。老规矩,我们依旧来看时间复杂度就会发现和上面插入一样,在删除操作的时候是O(1)级别的,但是查找位置的时候就有O(n)的时间复杂度。
6、创建单链表
上面列举了几个单链表的操作,初始化之后我们如何创建单链表呢,这里就有前插法和尾插法。
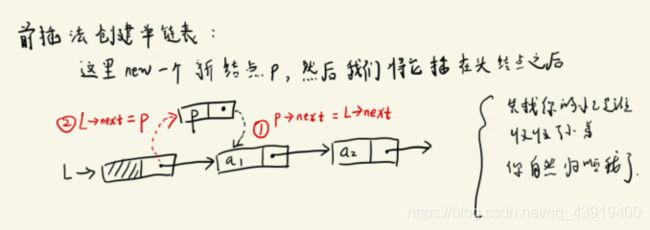
(1)我们先来看看前插法:前插法是通过将新结点逐个插入链表的头部(头结点之后)来创建链表,每次申请一个新结点,读入相应的数据元素值,然后将新结点插入到头结点之后。
图片右边的文字描述就是我在上面插入部分提及的我自己的理解,也就是先让新插入的节点去寻找插入位置的后一个结点,然后前一个结点再指向插入的节点就完成了插入。
void CreateList_H(LinkList &L,int n)
{
L=new LNode;
L->next=NULL;
for(i=0;i>p->data;
p->next=L->next;L->next=p;
}
} 这里和上面的插入没有什么不同,不一样的是使用for循环输入多个值而已,这里的时间复杂度显然就是for里面的规模,所以是O(n)。
(2)后插法创建单链表:后插法是通过将新结点逐个插入到链表的尾部来创建链表。
我们发现与前插法不一样的是,这里多了一个辅助指针r,其实就是为了指向最后一个结点,所以特地加的,其它部分都是有一样的。
void CreateList_R(LinkList &L,int n)
{
L=new LNode;
L->next=NULL;
r=L;
for(i=0;i>p->data;
p->next=NULL;r->next=p;
r=p;
}
} 这里可以按照我之前的习惯,上来就找后面的,所以为p->next=null,然后在r->next=p,最后让尾指针移位就好。如果你问我交换位置可以吗???当然可以啦,但是上图中(3)操作的位置绝对是不可以和(1)操作交换位置的,不然就出现p->next=p的操作啦,这个错误和上面的插入的错误是一样的(切记,不管是循环链表等等插入也好,一定要注意顺序问题)。
四、循环链表和静态链表
这里插入一点关于循环链表的小知识,所谓循环链表就是表中最后一个结点的指针域指向头结点,整个链表形成一个环(借用一下百度的图片,这里展示的是循环单链表,当然也有循环双链表,也就是双链表指向头结点就好)。
如果你把单链表弄的很透彻,通过画图也可以很好的掌握循环链表,这里就不在赘述。
至于静态链表你可以理解为一个二维数组,只是a[1]里面存储的是下一个结点的下标而已。具体的定义有:静态链表借助数组来描述线性表的链式存储结构,结点也有数据域data和指针域next,与前面所讲的链表中的指针不同的是,这里的指针是结点的相对地址(数组下标),又称游标。
五、双向链表(双链表)
想象一下我们如果要找到单链表中某个结点的直接后继直接通过next就找到了(已经得到了这个结点位置的指针),而要找直接后继却只可以从到到尾O(n)的时间复杂度。这个时候你就想,要是可以有一个往前指的指针该多好啊,所以我们就有了双向链表。
首先来看看存储结构吧:
typedef struct DuLNode
{
ElemType data;
struct DuLNode *prior;
struct DuLNode *next;
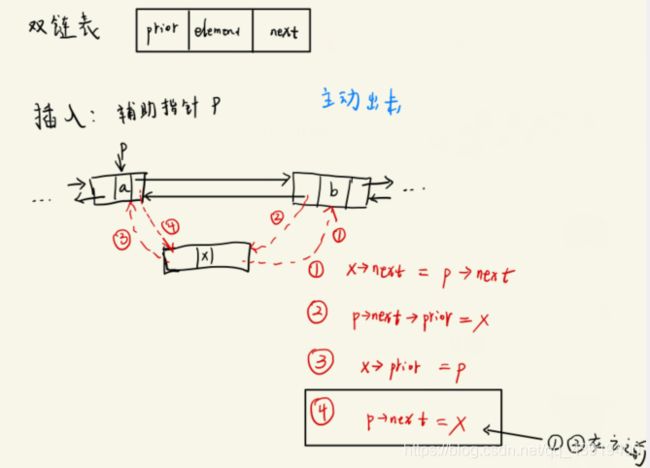
}DuLNode,*DuLinkList;我们发现就是多了一个指向直接前驱的指针而已,其中的具体操作我们来说说。
1、双向链表的插入
这里我依旧按照自己的习惯,先去找后面的“小弟”,然后再去找大哥。大家可以养成一个习惯,就是(1)(2)一起,(3)(4)一起,这样不会乱。而(4)操作要在(1)(2)操作之后其实很好理解,如果你认真看了我前面单链表的操作的话,就会发现,(4)操作对p->next做了定义,所以会影响到(1)和(2)操作。这一点不需要强行记忆,如果出现在题目中,你只需要看看顺序改变是否会影响赋值就好,而在写代码的话按照我上面的习惯是没有问题滴。
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e)
{
if(!(p=GetElem_Dul(L,i)))//在L中确定第i个元素的位置指针p
return ERROR;
s=new DuLNode;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}我们来看看时间复杂度,不就是O(n)吗?这里花费时间的就是查找了。
2、删除
双向链表的删除不也是一样的吗?先让p后继指向q的后继,然后将q后继的前驱指向p(这里我写出了a结点,小失误,不影响),最后释放q结点就好。
Status ListDelete_DuL(DuLinkList &L,int i)
{
if(!(p=GetElem_DuL(L,i)))
return ERROR;
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
return OK;
}我们看看时间复杂度,估计不用看了,就知道是O(n)了。
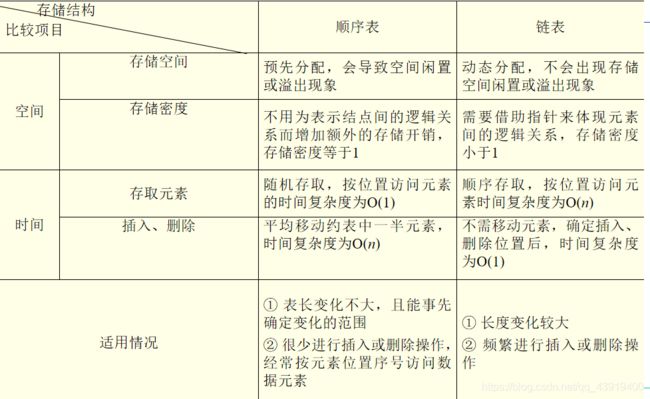
那么到这里关于线性表的基础知识就完结了,注意,这里只是基础部分,即使你完全看懂了,还是得多练,多写代码,在算法题中融会贯通呀。那么我们还是按照常规比较一下顺序表和单链表的操作吧,这里我偷懒,偷偷放图片就好了。
但是当知识遗忘大多数之后,我还是记得如果插入删除比较多就用链表,如果查找比较多就用顺序表,虽然不是绝对的,但是这句话总是经典呀!
后记:
如果你看到这里,这的辛苦啦!太棒了吧也,然后建议就是去多刷题吧,如果知识点有模糊的地方,一定不要忽略,自己画画图就可以弄懂了。下次见!