卷积神经网络基础知识

1. 卷积神经网络（CNN ）的发展史

• 1986年，Runmelheart和Hinton等人提出了反向传播算法（Back Propagation, BP）
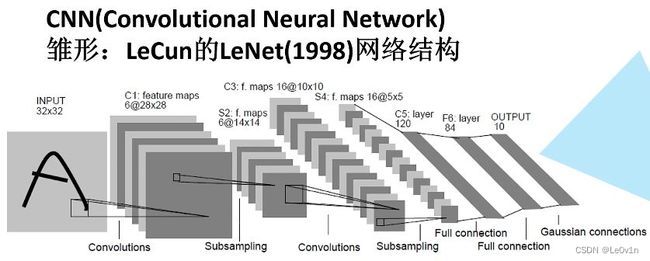
• 1998年，LeCun利用BP算法训练LeNet5网络，标志着CNN的真正面世（但此时的硬件水平很难去训练网络）
• 2006年，Hinton在他们的Science Paper中首次提出了Deep Learning的概念
• 2012年，Hinton的学生Alex Krizhevsky在寝室用GPU死磕了一个Deep Learning模型，一举摘下了视觉领域竞赛ILSVRC 2012的桂冠，在百万量级的ImageNet数据集合上，效果大幅度超过传统方法（70%多 -> 80%多）

2. 全连接层

说的简单直白一些，FC其实就是一个线性投影的操作，在FC后面一个非线性激活函数，那么可以使其拥有一定的非线性表达能力。

3. Back Propagation（BP）

BP算法包括①信号的前向传播和②误差的反向传播两个过程。即

• 计算误差输出时按“输入->输出”的方向进行
• 调整权值和阈值时则按“输出->输入”的方向进行

理论上，三层的BP神经网络可以实现多维单位立方体 ${\mathcal{R}}^m到{\mathcal{R}}^n$ 的映射，即能够逼近任何有理函数。

4. CNN中独特的层结构——卷积层 (Convolution Layer)

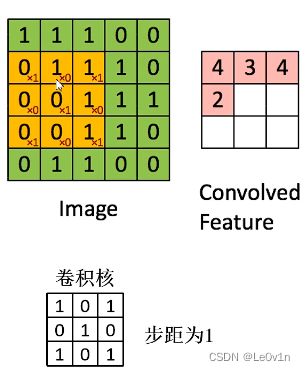
4. 1卷积的本质

卷积其实就是一个可以滑动的窗口在特征图上滑动并计算得到新特征图的操作。

4.2 卷积的目的

进行图像的特征提取

4.3 卷积的特性

1. 局部感知机制
2. 权值共享

4.3.1 局部感知机制

因为滑动窗口的大小是由卷积核大小决定的，一般使用的卷积核大小为 1×1, 3×3，5×5,…。所以一般比特征图要小，所以每次的计算只能计算窗口大小的值，即感知的大小只有窗口那么大

4.3.2 权值共享

我们知道，卷积核里面的是有值的，里面的值就确定了滑动窗口该如何进行计算。训练网络的目的主要是为了更新、优化卷积核里面的值。因为卷积具有局部感知的机制，所以需要多次滑动窗口才能浏览完整张特征图，而权值共享就意味着，并不是说每滑动一次窗口，卷积核里面的值要变一下，而是卷积核里面的值是固定的，3×3的卷积核里面就9个数，在卷积过程中不会变，只有反向传播时参数优化才会变。

4.4 权值共享的好处

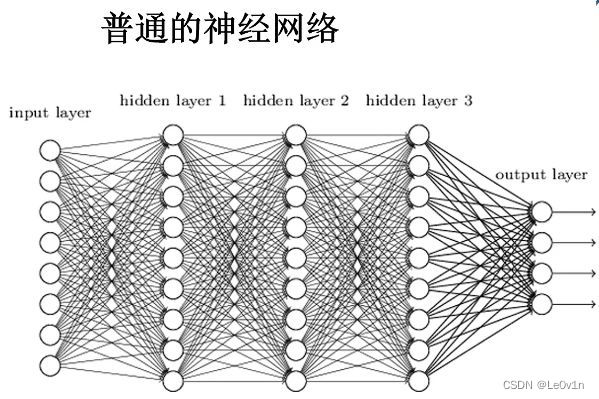
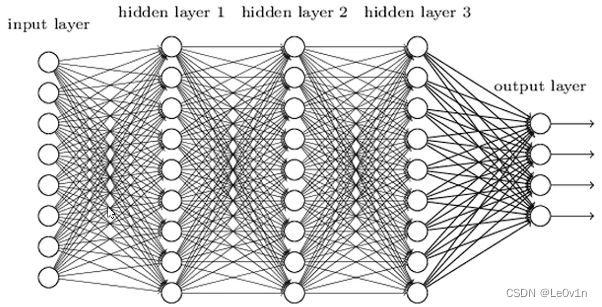
普通的BP神经网络
对于一张分辨率 1280×720 的图片，假设隐藏层1（hidden layer 1）的神经元个数为1000，那么图片经过第一个隐藏层后的参数数量为：
$$\begin{array}{rl}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{s}& =1280\times 720\times 1000\\ & =921,600,000\end{array}$$

这个参数量是巨大的（这也就是为什么现在的分类网络基本上不再使用FC作为分类头了）。而对于卷积神经网络来说，假设layer 1采用1000个5×5的卷积核，那么图片经过它后的参数数量为：
$$\begin{array}{rl}\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{s}& =5\times 5\times 1000\\ & =25,000\end{array}$$

可以看到，参数量大大减少。

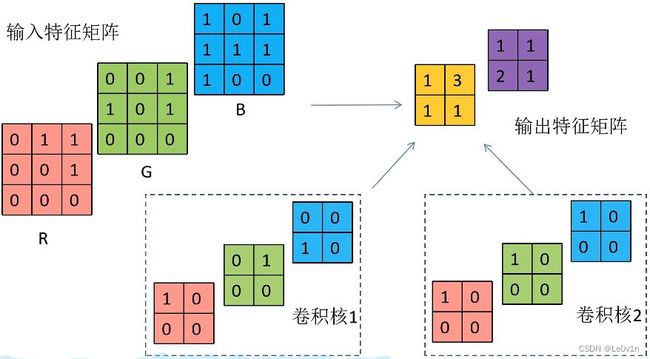
4.5 多通道卷积的使用

​

3通道输入的卷积示例

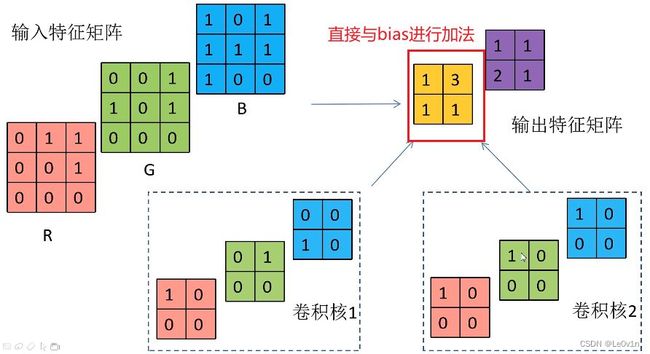
输入特征矩阵为3通道，为了保证可以计算，卷积核的维度应该也是3维。和特征图一样，卷积核也是一个多维tensor。而卷积核的数量决定了输出特征图的通道数。这就解释了为什么在代码，我们只需要指定输入通道数和输出通道数即可（卷积核的channel不需要我们指定）：

torch.nn.modules.conv.Conv2d 
        def __init__(self,
             in_channels: int,  # 输入通道数
             out_channels: int,  # 输出通道数，即卷积核的个数
             kernel_size: int | tuple[int, int],  # 卷积核的大小
             stride: int | tuple[int, int] = 1,  # 卷积核的步长
             padding: str | int | tuple[int, int] = 0,  # 卷积核的填充大小
             dilation: int | tuple[int, int] = 1,  # 空洞卷积的空洞率大小
             groups: int = 1,  # 卷积时分组的个数
             bias: bool = True,  # 是否存在偏置
             padding_mode: str = 'zeros',  # 填充时使用的模式
             device: Any = None,  # 负责进行此操作的设备（CPU、GPU、DP、DDP）
             dtype: Any = None) -> None  # 数据类型

1. in_channels: 输入通道数，即输入特征图的的通道数 -> 目的是给卷积核分配对应的维度 。
   假设输入为(channel, height, width)=(32, 28, 28)，那么卷积核会根据in_channels参数来指定卷积核，即卷积核为(channel, height, width) = (32, kernel_size[0], kernel_size[1])
2. out_channels：输出通道数，即输出特征图的通道数 -> 目的是告诉卷积核分配几个卷积核去进行运算，因为一个卷积核只能生成一个单通道feature，最后进行维度的拼接，得到out_channels维度大小的输出特征图。
3. kernel_size：卷积核滑动窗口的大小。

小结：

1. 卷积核的channel与输入特征图的channel要相同（写代码时不用考虑）
2. 输出特征图的维度与卷积核的个数相同（out_channels即为卷积核的个数，也是输出特征图的通道数）

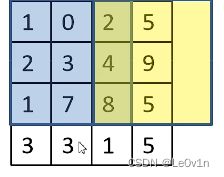
4.6 加了bias的卷积运算

非常简单，就是输入特征图直接加上bias就可以了。

​

4.7 加了激活函数的卷积运算

4.7.1 前置知识——常用的非线性激活函数

Q: 为什要引入非线性激活函数？
A: 引入非线性因素，使其具备解决非线性问题的能力。

---

4.7.2 常用的激活函数

Sigmoid

Sigmoid激活函数饱和（值接近1或-1）时梯度值非常小，故网络层数较深时易出现梯度消失的问题。

ReLU

缺点在于当反向传播过程中有一个非常大的梯度经过时，反向传播更新后可能导致权重分布中心小于零，导致该处的倒数始终为0，反向传播无法更新权重，即进行失活状态。
​

从上图可以看到，对于Sigmoid激活函数来说，当函数值很大/小时，导数就趋近于0了 -> 可能导致梯度消失的问题。

4.8 卷积核越界处理

​

在卷积操作过程中，矩阵经卷积操作后的尺寸由以下几个因数决定：

1. 输入视频大小W×W
2. 卷积核大小F×F
3. 步长S
4. padding的像素数P

经卷积后的矩阵尺寸大小计算公式为：
$$N=\frac{(W-F+2P)}{S+1}$$

5. 池化层（Pooling）

目的：对特征图进行稀疏处理，减少数据运算量。

特点：

1. 没有训练参数
2. 没有卷积核，所以没有可以学习的参数——本质上就是一个运算
3. 只改变特征矩阵的 w 和 h ，不改变channel
4. 没有卷积核，也就谈不上改变channel了（卷积核个数 = 输出的channel），但是有pool kernel，可以改变特征图的尺寸
5. 一般pool size和stride相同

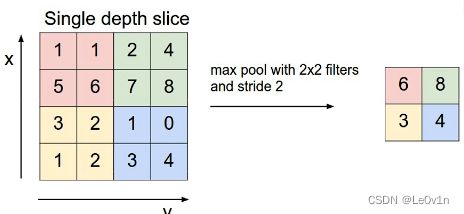
5.1 MaxPooling

​

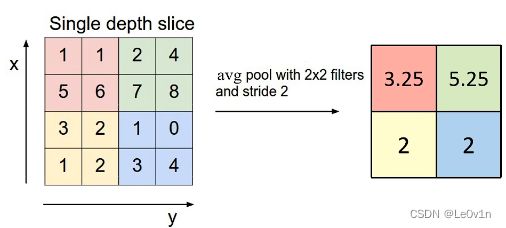
5.2 Average Pooling

​

6. Loss的计算

​

3层的BP神经网络计算流程图

• 第一层：输入层
• 中间层：隐藏层
• 第三层：输出层
  ​
  

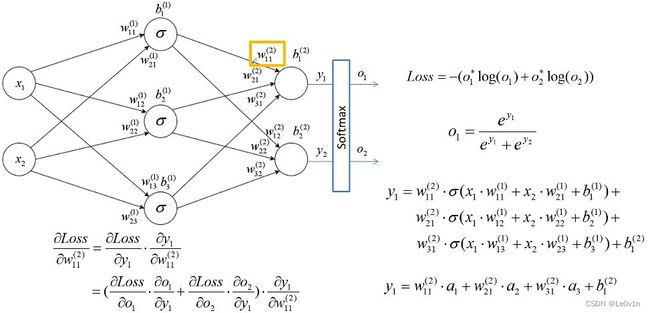
隐藏层第一个节点的计算

输出的计算

6.1 Softmax激活函数的计算过程

性质：经过sofmax处理后所有输出节点概率之和为1。

公式：

$$o_i=\frac{e^{y_i}}{{\sum }_j{e}^{y_i}}$$
​

经过BP神经网络输出的 $y_1,y_2$ 其实并不符合概率的分布，而一般情况下我们想要得到的是一个概率的输出，所以我们使用Softmax激活函数对其进行处理得到概率分布。

6.2 Cross Entropy Loss，交叉熵损失函数

6.2.1 针对多分类问题（softmax输出，所有输出概率之和为1）

$$H=-\sum _i{o}_i^{\ast }\ln o_i$$

6.2.2 针对二分类问题（sigmoid输出，每个输出节点之间互不相干）

$$H=-\frac{1}{N}\sum _{i=1}^N[o_i^{\ast }\ln o_i+(1-o_i^{\ast })\ln (1-o_i)]$$

其中 $o_i^{\ast }$ 为真实标签值（GT）， $o_i$ 为预测值，默认$\log$以$e$为底等于$\ln$。

• 采用Softmax输出则符合概率输出（所有概率之和为1）
• 采用Sigmoid输出则不符合概率输出

根据公式我们可以得到Loss使用交叉熵的计算公式。
​

7. Loss的反向传播

在得到Loss后我们需要对Loss进行反向传播。
​

正向传播的计算函数我们已经知道了，根据这个函数我们进行链式求导就可以得到梯度的计算公式。

先对$y1$求导再对$w_{11}$求导

接下来对表达式中的每一个偏导进行计算：
​

这样我们就可以得到每一个节点的损失梯度。接下来我们需要根据梯度进行权值的更新。

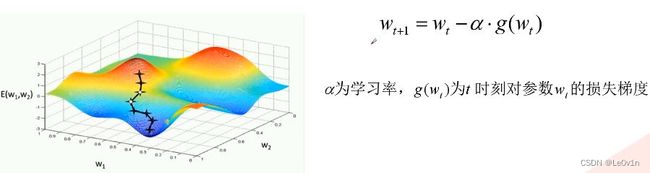
8. 权值更新

​

更新权重的表达式非常简单，但是我们无法确定所求的梯度方向是不是减少损失最快的方向。

​
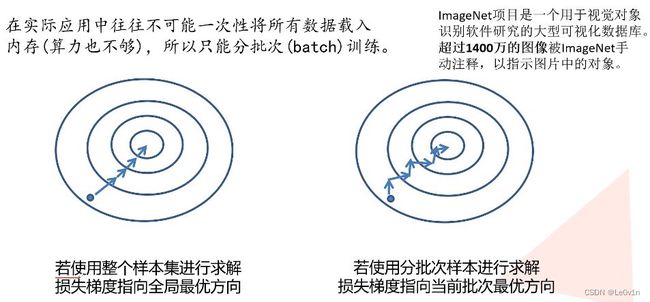
在实际训练中，我们往往是设置batch进行训练的，每一个批次训练完毕后会计算该批次的Loss以及梯度，虽然有梯度，但这个梯度是对于这一个批次来说是最优的，对于整个数据而言就不一定的。所以为了更好的在batch训练中进行梯度更新，引入了优化器（optimizer）的概念。

9. 优化器（optimizer）

​

一般常用的优化器有：

• SGD
• SGD + Momentum
• Adagrad
• RMSProp
• Adam

使用优化器的目的是为了使网络更快的收敛。

9.1 SGD（Stochastic Gradient Descent）

​

SGD的缺点：

• 易受样本噪声影响
• 有些标签是错误的，SGD会受到较大的影响
• 可能陷入局部最优解

9.2 SGD+Momentum

​
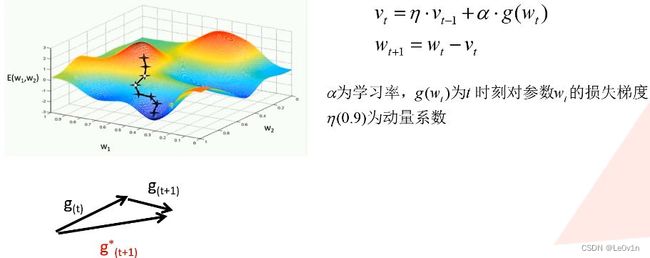
除了计算当前batch的梯度外还会加入之前batch的梯度。

$g_{(t+1)}$ 为本次batch的梯度， $g_{(t)}$为上一个batch的梯度，$g_{(t+1)}^{\ast }$ 为本次batch实际更新的梯度。

加了动量可以有效抑制样本噪声的干扰。

9.3 Adagrad（自适应学习率）

该优化器是对学习率进行改进的。
​

随着batch的进行，最终 $\frac{\alpha }{\sqrt{s_t+ϵ}}$ 会越来越小 -> 代表着更新的力度越来越小，看起来就像更新时用到的学习率逐渐变小了。

Adagrad缺点：

• 学习率下降太快，可能还没有收敛就停止训练了。

9.4 RMSProp（自适应学习率）

也是对学习率进行调整，是Adagrad优化器的改进版本。相比于Adagrad优化器，RMSProp其实就是添加了两个系数去控制学习率的衰减力度。
​

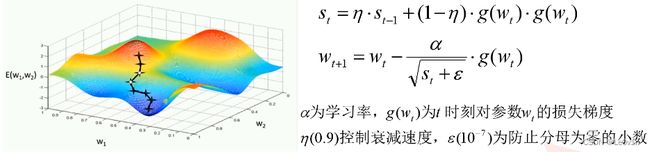
9.5 Adam（自适应学习率）

​

9.6 几种优化器效果对比

9.6.1 速度比较

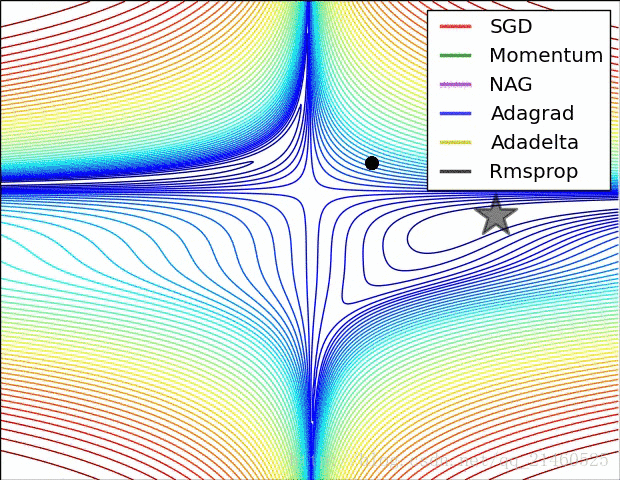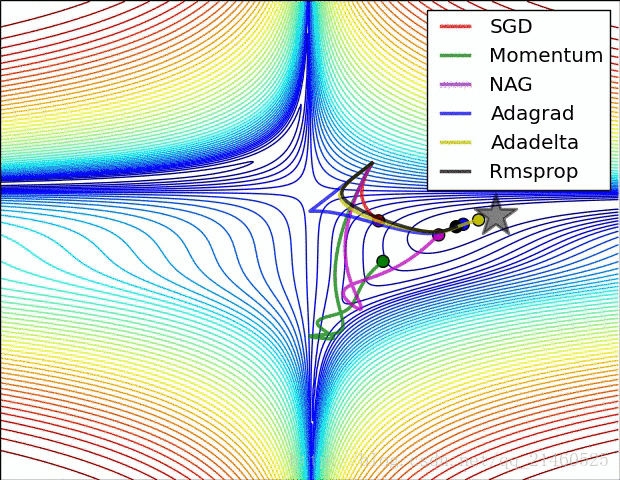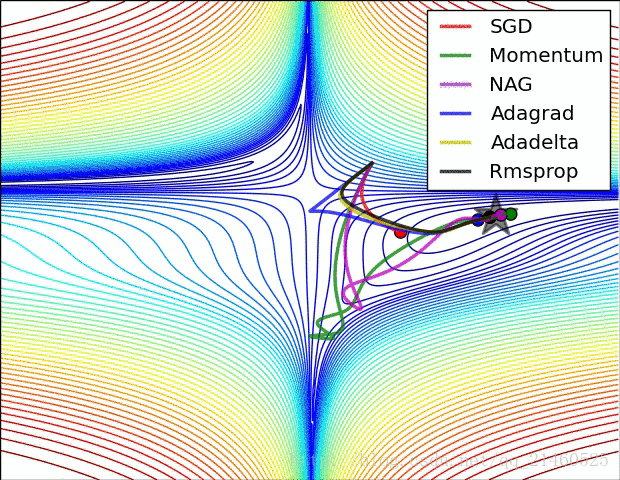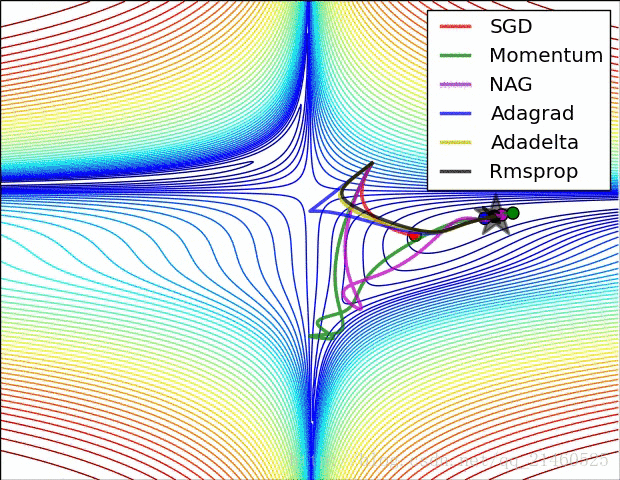
9.6.2 在鞍点的性能比较

9.7 优化器总结

• SGD虽然速度慢，但梯度更新的方向是比较理想的。
• 带有Momentum的SGD开始时不好，但很快找回了正确的路径
• Adagrad和RMSProp不仅方向保持是正确的，而且速度也很快

这里没有展示Adam优化器的效果

9.8 优化器推荐

在实际项目中，比较常用的有：

• 带有Momentum的SGD
• Adam

可能有很多人选择使用Adam优化器，因为它的效果比较好，但是在论文中，很多作者仍然使用的是带有momentum的SGD优化器

如何选择还是要看实际情况

参考

1. https://www.bilibili.com/video/BV1b7411T7DA?spm_id_from=333.999.0.0
2. https://github.com/vdumoulin/conv_arithmetic
3. https://blog.csdn.net/weixin_44878336/article/details/124869795