matlab 编写计算傅里叶系数函数
1. 编写计算傅里叶级数系数的函数
%计算函数 x 的 N 次谐波的傅里叶级数系数,函数的周期为 T0
%数组 X 存放的是傅里叶系数,也就是幅值
%数组 w 存放的是频率
function [X, w]=fourierseries(x, T0, N)
syms t;%因为传进来的x函数中包含符号 t,所以函数内部也要定义符号变量 t,否则会报错
for k = 1: N,
X(k)=int(x*exp(-j*2*pi*(k-1)*t/T0), t, 0, T0)/T0;
w(k)=(k-1)*2*pi/T0;
end
end
X(k) = int(x*exp(-j*2*pi*(k-1)*t/T0), t, 0, T0) / T0;
上面的式子为傅里叶公式
X ( k ) = 1 T 0 ∗ ∫ 0 T 0 x ( t ) ∗ e − j ∗ k ∗ Ω 0 ∗ t d t X(k) =\frac{1}{T0}* \int_{0}^{T0}x(t) * e^{-j*k*\Omega_0*t}dt X(k)=T01∗∫0T0x(t)∗e−j∗k∗Ω0∗tdt
其中使用了计算积分的 int 函数,不懂使用的可以看这里 matlab 使用 int函数 求积分
2*pi*(k-1)*/T0
注意上面的意思是 ( k − 1 ) ∗ Ω 0 (k-1)*\Omega_0 (k−1)∗Ω0 ,因为频率要从 0 开始每次递增 Ω 0 \Omega_0 Ω0,K 是从 1 开始,所以要 -1。
w(k) = (k-1)*2*pi/T0;
这行代码的意思是 w ( k ) = ( k − 1 ) ∗ Ω 0 w(k) = (k-1)*\Omega_0 w(k)=(k−1)∗Ω0,因为频率要从 0 开始每次递增 Ω 0 \Omega_0 Ω0,K 是从 1 开始,所以要 -1。
下面我们可以使用上面编写好的函数计算函数的N次谐波对应的傅里叶系数和相位
2. 求 y = s i n ( 5 ∗ t ) y=sin(5*t) y=sin(5∗t) 的5次谐波(谐波次数可以任意指定)
clear all;
syms t;
y=sin(5*t); T0 = 2 * pi/5; N=5;
figure(1);
subplot(211);
ezplot(y , [0, 2*pi]);
grid;
[Y1, w1] = fourierseries(y, T0, N);
disp(Y1);
disp(w1);
%fliplr(Y1(2:N))的意思是将Y1数组中第2到N个数字顺序反转
%比如 Y1 数组为 [ 0, -1i/2, 0, 0, 0]
%fliplr(Y1(2:N))) 得到就是 [ 0, 0, 0, -1i/2]
%conj函数是求共轭
%比如对数组 [ 0, 0, 0, -1i/2] 求共轭,得到的就是 [ 0, 0, 0, 1i/2]
Y = [conj(fliplr(Y1(2:N))) Y1];
w = [-fliplr(w1(2:N)) w1];
disp(Y);
disp(w);
subplot(223);
stem(w, abs(Y));%abs函数是对数组 Y 的每一个元素取绝对值
subplot(224);
stem(w, angle(Y));%angle函数是对数组 Y 的每一个元素求其对应的弧度
%计算函数 x 的 N 次谐波的傅里叶级数系数,函数的周期为 T0
%数组 X 存放的是傅里叶系数,也就是幅值
%数组 w 存放的是频率
function [X, w]=fourierseries(x, T0, N)
syms t;%因为传进来的x函数中包含符号 t,所以函数内部也要定义符号变量 t,否则会报错
for k = 1: N,
X(k)=int(x*exp(-j*2*pi*(k-1)*t/T0), t, 0, T0)/T0;
w(k)=(k-1)*2*pi/T0;
end
end
下面,我们在刚才的函数上面增加 1
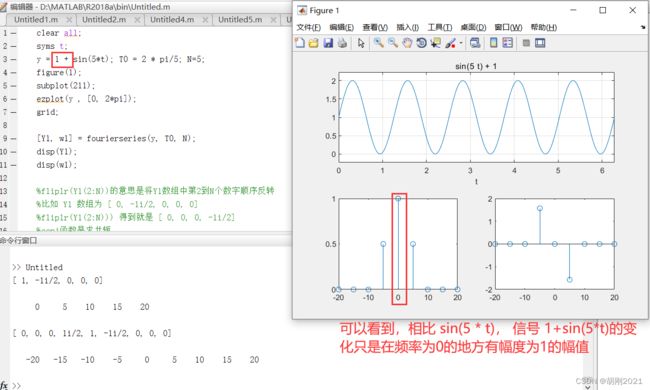
3. 求 y = 1 + s i n ( 5 ∗ t ) y=1+sin(5*t) y=1+sin(5∗t) 的5次谐波(谐波次数可以任意指定)
只需在原来的信号函数前面加 1 即可
4. 求 y = 2 + s i n ( 5 ∗ t ) y=2+sin(5*t) y=2+sin(5∗t) 的5次谐波(谐波次数可以任意指定)
只需在原来的信号函数前面加 2 即可