因子分析之ggplot2
R语言因子分析与ggplot2
- 一、mvstats包与本文所用的数据
-
- 1.mvstats包
- 2.本文所用的数据
- 二、检验是否适合做因子分析
-
- 1.KMO检验巴特利特球形度检验
- 2.相关系数检验
- 3.相关系数热力图
- 三、因子提取
-
- 1.因子载荷图
- 四、计算因子得分
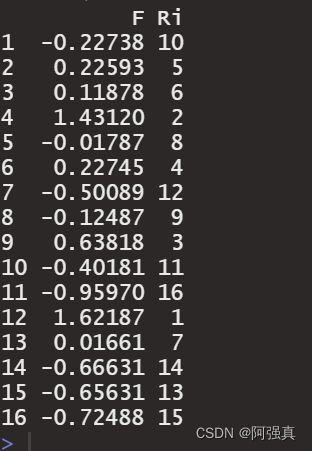
- 五、综合评价:
一、mvstats包与本文所用的数据
1.mvstats包
可能大家找不到mvstats包
链接:https://pan.baidu.com/s/1PdCMRwN9kGAg8u41pd5tYQ?pwd=upem
提取码:upem
打开后在R里面运行一下:在右侧就可以看到factpc这个函数了
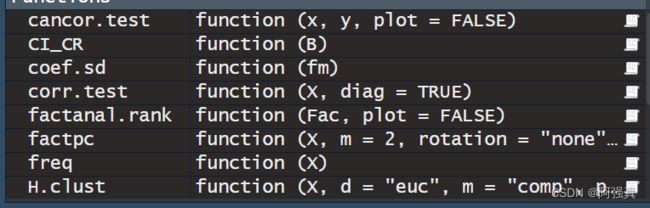
source("mvstats.R")#把数据和mvstats包放在同一目录下
a<-read.csv("ex6.6.csv",header=T,encoding="utf-8");a
如果调用mvstats失败,看下面:
事实上,我们只需要这一个函数。也可以把这个函数单独的提取出来,
factpc<-function(X, m=2,rotation="none",scores="regression")
{
options(digits=4)
S=cor(X);
p<-nrow(S); diag_S<-diag(S); sum_rank<-sum(diag_S)
#rowname<-paste("X", 1:p, sep="")
rowname = names(X)
colname<-paste("Factor", 1:p, sep="")
A<-matrix(0, nrow=p, ncol=p, dimnames=list(rowname, colname))
eig<-eigen(S)
for (i in 1:p)
A[,i]<-sqrt(eig$values[i])*eig$vectors[,i]
for (i in 1:p) { if(sum(A[,i])<0) A[,i] = -A[,i] }
h<-diag(A%*%t(A))
rowname<-c("SS loadings", "Proportion Var", "Cumulative Var")
B<-matrix(0, nrow=3, ncol=p, dimnames=list(rowname, colname))
for (i in 1:p){
B[1,i]<-sum(A[,i]^2)
B[2,i]<-B[1,i]/sum_rank
B[3,i]<-sum(B[1,1:i])/sum_rank
}
#cat("\nFactor Analysis for Princomp: \n\n");
#cat("\n"); print(B[,1:m]);
W=B[2,1:m]*100;
Vars=cbind('Vars'=B[1,],'Vars.Prop'=B[2,],'Vars.Cum'=B[3,]*100)
#cat("\n"); print(Vars[1:m,])
#cat("\n"); print(A[,1:m]);
A=A[,1:m]
#{ cat("\n common and specific \n"); print(cbind(common=h, spcific=diag_S-h)); }
if(rotation=="varimax")
{
#stop(" factor number >= 2 !")
cat("\n Factor Analysis for Princomp in Varimax: \n\n");
VA=varimax(A); A=VA$loadings;
s2=apply(A^2,2,sum);
k=rank(-s2); s2=s2[k];
W=s2/sum(B[1,])*100;
Vars=cbind('Vars'=s2,'Vars.Prop'=W,'Vars.Cum'=cumsum(W))
rownames(Vars) <- paste("Factor", 1:m, sep="")
#print(Vars[1:m,])
A=A[,k]
for (i in 1:m) { if(sum(A[,i])<0) A[,i] = -A[,i] }
A=A[,1:m];
colnames(A) <- paste("Factor", 1:m, sep="")
#cat("\n"); print(A)
}
fit<-NULL
fit$Vars<-Vars[1:m,]
fit$loadings <- A
X=as.matrix(scale(X));
PCs=X%*%solve(S)%*%A
#if(scores) cat("\n"); print(PCs)
fit$scores <- PCs
#if(rank)
{
W=W/sum(W);
PC=PCs%*%W;
#cat("\n"); print(cbind(PCs,'PC'=PC[,1],'rank'=rank(-PC[,1])))
Ri=data.frame('F'=PC,'Ri'=rank(-PC))
fit$Rank <- Ri
}
#if(plot)
#{ plot(PCs);abline(h=0,v=0,lty=3); text(PCs,label=rownames(PCs),pos=1.1,adj=0.5,cex=0.85) }
#if(biplot)
#{ biplot(PCs,A) } #text(PCs,label=rownames(PCs),pos=1.1,adj=0.5,cex=0.85)
common=apply(A^2,1,sum);
fit$common <- common
fit
#list(Vars=B[,1:m],loadings=A,scores=PCs,Ri=Ri,common=common)
} #fa=factpc(X,2)
然后运行一下这个函数,就可以做因子分析了
2.本文所用的数据
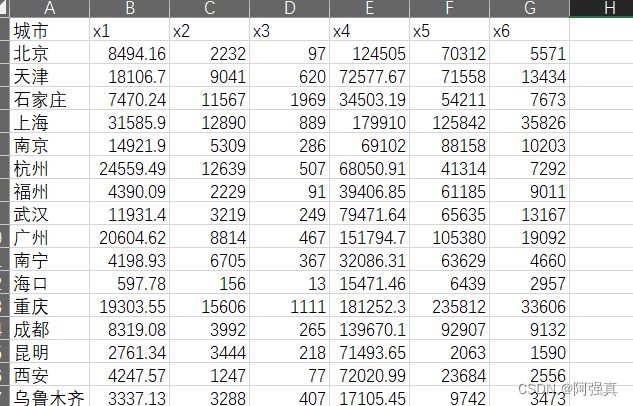
下表给出了2017年我国部分主要城市废水中主要污染物排放量数据,它们分别是:工业废水排放量x1(万吨)、工业化学需氧量排放量x2(吨)、工业氨氮排放量T3(吨)、城镇生活污水排放量x4(万吨)、生活化学需氧量排放量xs(吨)和生活氨氮排放量x6(吨).请根据这16个城市的废水中污染物排放量数据对这六个指标进行因子分析.
链接:https://pan.baidu.com/s/1DsaEkscGSRuml2wYx7Ke6A?pwd=i8hx
提取码:i8hx
二、检验是否适合做因子分析
1.KMO检验巴特利特球形度检验
install.packages("psych")
library(psych)#KMO和Bartlette所需要的包
b<-a[,-1];b#去除第一列,列名
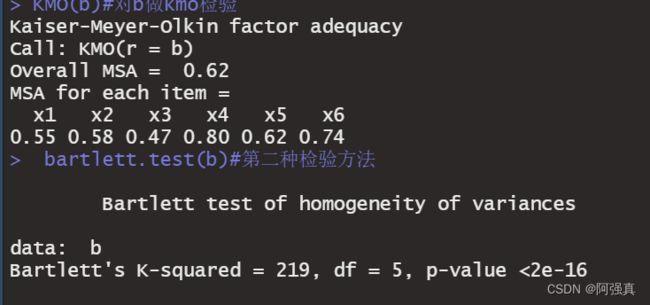
KMO(b)#对b做kmo检验
bartlett.test(b)#巴特利特球形度检验
KMO值为0.62,大体上可以做
巴特利特球形度检验的p值小于0.05即认为可以
如果你认为上面不够酷的话,可以看下面两种方法:
2.相关系数检验
一般来说,大部分变量的相关系数在0.3到0.9之间才可以做因子分析,不然的话就是弱相关或者会产生多重共线性
install.packages("qgraph")
library(qgraph)#相关系数网络图,
(corr<-cor(b))#做协方差矩阵
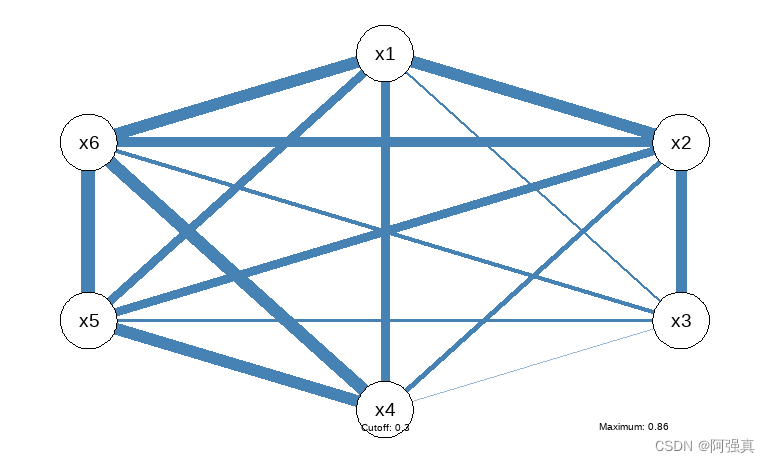
qgraph(corr,details=T,cut=0.3,posCol="steelblue")#网络图,相关性越强颜色越深,线越宽
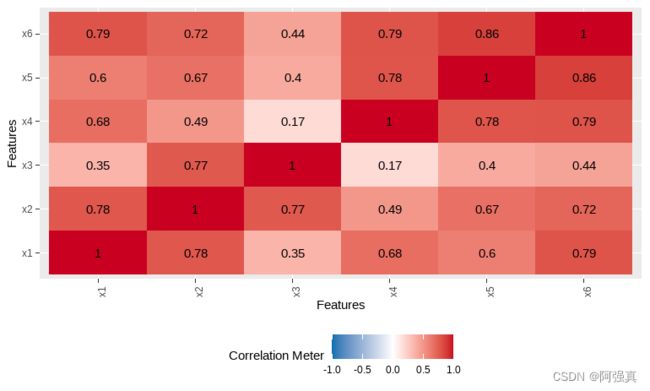
3.相关系数热力图
install.packages("DataExplorer")
library(DataExplorer)
plot_correlation(b,type="c")
三、因子提取
现在有6个变量,首先尝试提取两个因子,看累计方差贡献率是否达到了80%,没有在提取
fac=factpc(b,2)
fac$Vars

可以看出前两个因子的累计方差贡献率已经达到了86%,因此可以尝试提取两个因子。但是在实际问题中,一般这样提取的因子可能命名不具有解释性,需要做因子正交旋转(这里基于主成分法采用方差最大化做)使因子的命名更具有解释性。
(fac1=factpc(scale(b),2,rot="varimax"))
scale(b)对原始数据标准化,这个应该一开始就要做,不过没关系,影响不大,读者自己写的话,如果数据相差很大,或者是单位不同,第一步先标准化。rot=“varimax”是方差最大化
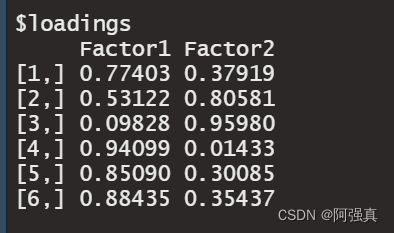
通过因子载荷可以得出:
F 1 = 0.7 x 1 + 0.5 x 2 + 0.09 x 3 + 0.94 x 4 + 0.85 x 5 + 0.8 x 6 F 2 = 0.3 x 1 + 0.8 x 2 + 0.9 x 3 + 0.01 x 4 + 0.3 x 5 + 0.3 x 6 F_1=0.7x_1+0.5x_2+0.09x_3+0.94x_4+0.85x_5+0.8x_6 \\ F_2=0.3x_1+0.8x_2+0.9x_3+0.01x_4+0.3x_5+0.3x_6 F1=0.7x1+0.5x2+0.09x3+0.94x4+0.85x5+0.8x6F2=0.3x1+0.8x2+0.9x3+0.01x4+0.3x5+0.3x6
可以看出F1在x1,x4,x5,x6上载荷较高,可命名为A因子(我没啥文化,就用A代替),同理F2可命名为B因子
1.因子载荷图
kjl<-data.frame(fac1$loadings,row.names=colnames(a)[-1]);kjl#旋转后的因子载荷矩阵
score=fac1$scores#提取因子得分
ggplot(kjl,aes(Factor1,Factor2,colour=loading))+geom_point(size=4,shape=18)+geom_text_repel(aes(label=j),size=4
)+geom_hline(yintercept = 0,linetype="longdash",col=4)+geom_vline(xintercept = 0,linetype="longdash",col=4
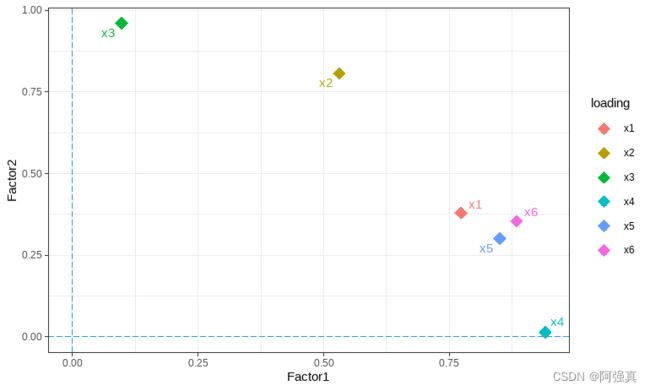
根据变量间距离的远近可以把x1,x4,x5,x6归为A因子,剩下的归为B因子
四、计算因子得分
score=fac1$scores#提取因子得分
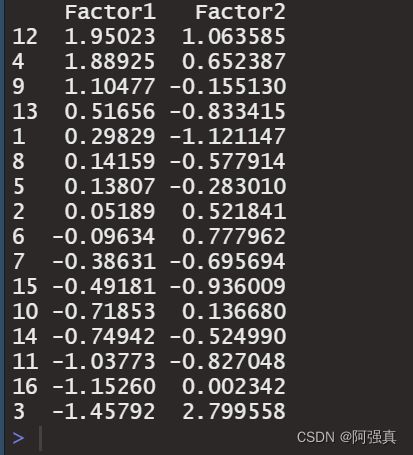
score1=score[order(score[,1],decreasing = T),];score1
因子得分图:
score<-data.frame(score)
rownames(score)<-a[,1];score
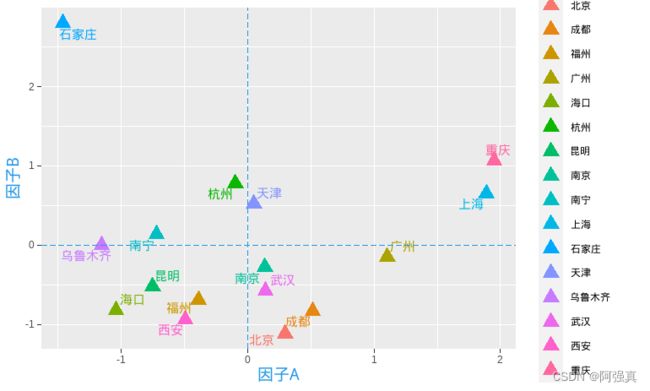
ggplot(score,aes(Factor1,Factor2,colour=rownames(score)))+
geom_point(size=4,shape=17)+geom_text_repel(aes(label=a[,1]),size=4)+
theme(plot.title=element_text(hjust=0.5))+
geom_hline(yintercept = 0,linetype="longdash",col=4)+
geom_vline(xintercept = 0,linetype="longdash",col=4)+
xlab("因子A")+ylab("因子B")+
theme(axis.title.y=element_text(size = 14,color=4),axis.title.x=element_text(size = 14,color=4))