【小波理论及其应用】
小波理论结束及其应用
- 1. 傅里叶变换和短时傅里叶变换的局限性
- 2. 小波理论简介--小波变换
-
- 2.1 连续小波变换(CWT)
- 2.2 离散小波变换(DWT)
- 3. 小波滤波器组理论
- 4. 小波应用
- 5. MATLAB中的小波
-
- 5.1 举例1---分解
- 5.2 举例2---分解细节重构
- 5.3 举例3---分解重构
1. 傅里叶变换和短时傅里叶变换的局限性
- 将信号f(T)分解为无穷多个正弦波/余弦波(谐波)；
- 没有办法准确地识别事件发生的地点；
- 不能很好地处理不连续的、突发的信号，例如视频，音乐等。
-
平稳信号
频率含量在时间上不变的信号
所有频率分量在任何时候都存在 -
非平稳信号
频率分量随时间的变化
一个例子：“Chirp信号”
频率分量是什么时候发生的？“傅里叶变换”看不出来！
短时傅里叶痛点：
为了克服傅里叶变换无法实现时域局部化，以及 STFT存在固定分辨率的缺陷，希望窗口函数的形状可以改变，即在低频部分具有较高的频率分辨率和较低的时间分辨率，而在高频部分具有较高的时间分辨率和较低的频率分辨率，由此引出下节小波变换。
2. 小波理论简介–小波变换
小波变换由法国地球物理学家 Morlet于 20世纪 80年代初在分析地球物理信号时提出。小波变换优于傅里叶变换的地方：在时域和频域同时具有良好的局部化性质。而且由于对高频成分采用逐渐精细的时域或空域采样步长，从而可以聚焦到对象的任意细节，故被人们誉
为数字显微镜。
2.1 连续小波变换(CWT)
假设母函数为 
，定义伸缩、平移变量为 , a，b ∈R且 0>a ，则簇函数为
若信号为 
，则 x(t)的小波变换为
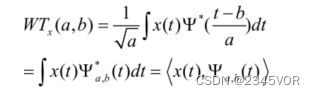
- 在小波变换中，在每一个可能的尺度上计算小波系数是一项相当大的工作，它产生了大量的数据。
- 如果尺度(A)和位置(B)被选择为离散的，那么分析就会容易得多，不会产生大量的数据。
- 这种选择离散值展开(A)和平移(B)参数的思想在
冗余小波变换
小波正交基/多解析度分析
2.2 离散小波变换(DWT)
即在 (a ,b ) 离散网格上作小波变换，称为离散小波变换 ( DWT)。
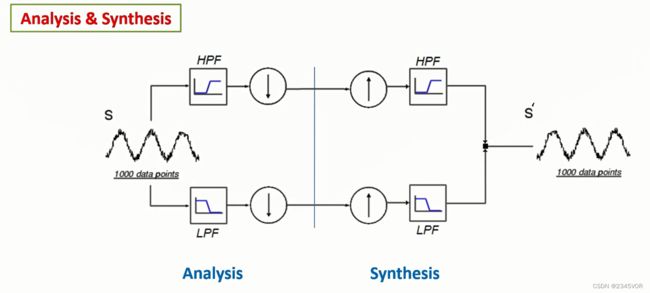
3. 小波滤波器组理论
小波分类
小波适用范围
—系列用于研究高维空间特征的方向性小波
4. 小波应用
小波在压缩，消噪，不连续检测，特征增强都有运用。
5. MATLAB中的小波
小波分解与重构基本函数
[c,l]=wavedec(s,N,'wname') 对信号s进行一维N尺度分解
x=waverec(c,l,'wname') 用指定的小波函数'wname'对小波分解结构(c,l)进行多尺度一维小波重构
A=appcoef(c,l,'wname',N) 计算尺度N时的低频系数。
D=detcoef(c,l,N) 提取N尺度的高频系数。
[nc,nl,ca]=upwlev(c,l,'wname')对小波分解结构[c,l]进行单尺度重构，返回上一尺度的分解结构并提 取最后一尺度的低频分量。
x=wrcoef('type',c,l,'wname',N)对一维信号的分解结构[c,l]用指定的小波函数进行重构，当'type=a' 时对信号的低频部分进行重构，此时N可以为0.当'type=d'时，对信号 的高频部分进行重构，此时N为正整数。
y=upcoef('O',x,'wname',N) 用于一维小波分析，计算向量x向上N步的重构小波系数，N为正整数。如 果O=a,对低频系数进行重构；如果O=d，对高频系数进行重构。
[thr,sorh,keepapp]=ddencmp('den','wv',x)产生信号全局默认阈值，然后利用wdencmp函数进行消除噪 声的处理,thr = sqrt(2*log(n)) * s
xd=wdencmp('gbl',x,'db3',2,thr,sorh,keepapp)
THR=wbmpen(C,L,SIGMA,ALPHA)使用penalization方法为降噪返回全局门槛THR.
5.1 举例1—分解
读取系统leleccum函数抽取1000份，
代码：
clc;clear;
load leleccum;
N=1000;
y = leleccum(1:N);
figure(1);
plot(y);
图像：
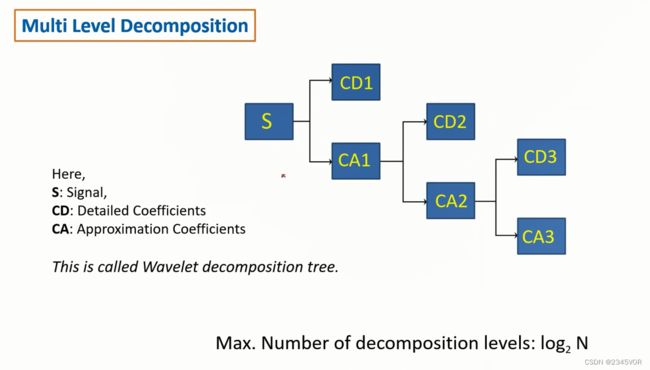
分别采用“db1”和“db3”进行3次分解
小波树如下：
第一级分解：
后级分解：
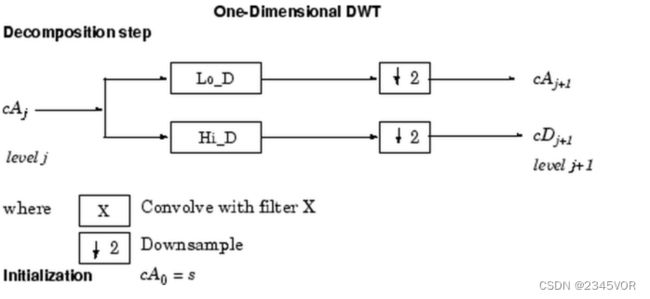
代码如下：
clc;clear;
load leleccum;
N=1000;
y = leleccum(1:N);
[c,l]=wavedec(y,3,'db1');
a3=appcoef(c,l,'db1',3);
d1=detcoef(c,l,1);
d2=detcoef(c,l,2);
d3=detcoef(c,l,3);
figure(1);
subplot(2,2,1)
plot(a3);
title('a3');
subplot(2,2,2)
plot(d3);
title('d3');
subplot(2,2,3)
plot(d2);
title('d2');
subplot(2,2,4)
plot(d1);
title('d1');
hold on;
[c,l]=wavedec(y,3,'db3');
a3=appcoef(c,l,'db3',3);
d1=detcoef(c,l,1);
d2=detcoef(c,l,2);
d3=detcoef(c,l,3);
figure(2);
subplot(2,2,1);
plot(a3);
title('a3');
subplot(2,2,2);
plot(d3);
title('d3');
subplot(2,2,3);
plot(d2);
title('d2');
subplot(2,2,4);
plot(d1);
title('d1');
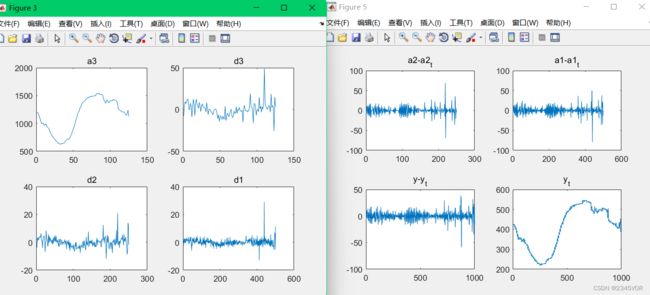
显示效果如下：
笔者可见“db1”比“db3”更加平滑，消除更多的高频噪声。
5.2 举例2—分解细节重构
“db1”先分解后重构
代码：
clc;clear;
load leleccum;
N=1000;
y = leleccum(1:N);
h=wfilters('db1','l'); % 低通
g=wfilters('db1','h'); % 高通
a1=dyaddown(conv(y,h)); % 卷积下采样
d1=dyaddown(conv(y,g)); % 卷积下采样
a2=dyaddown(conv(a1,h)); % 卷积下采样
d2=dyaddown(conv(a1,g)); % 卷积下采样
a3=dyaddown(conv(a2,h)); % 卷积下采样
d3=dyaddown(conv(a2,g)); % 卷积下采样,
figure(3);
subplot(2,2,1)
plot(a3);
title('a3');
subplot(2,2,2)
plot(d3);
title('d3');
subplot(2,2,3)
plot(d2);
title('d2');
subplot(2,2,4)
plot(d1);
title('d1');
d3_up=dyadup(d3); % 上采样
a3_up=dyadup(a3); % 上采样
d3_up=d3_up(1,[1:N/4]); % 去掉最后一个零
a3_up=a3_up(1,[1:N/4]); % 去掉最后一个零
hr=h(end:-1:1); % 重构低通
gr=g(end:-1:1); % 重构高通
hr=circshift(hr',1)'; % 位置调整圆周右移一位
gr=circshift(gr',1)'; % 位置调整圆周右移一位
a2_t=conv(a3_up,hr)+conv(d3_up,gr);
a2_t=a2_t(1,[2:end]);
a2_up=dyadup(a2_t);
d2_up=dyadup(d2);
d2_up=d2_up(1,[1:N/2]); % 去掉最后一个零
a2_up=a2_up(1,[1:N/2]); % 去掉最后一个零
a1_t=conv(a2_up,hr)+conv(d2_up,gr);
a1_t=a1_t(1,[2:end]);
a1_up=dyadup(a1_t);
d1_up=dyadup(d1);
d1_up=d1_up(1,[1:N]); % 去掉最后一个零
a1_up=a1_up(1,[1:N]); % 去掉最后一个零
y_t=conv(a1_up,hr)+conv(d1_up,gr);
y_t=y_t(1,[2:end]);
figure(5);
subplot(2,2,1)
plot(a2-a2_t);
title('a2-a2_t');
subplot(2,2,2)
plot(a1-a1_t);
title('a1-a1_t');
subplot(2,2,3)
plot(y-y_t);
title('y-y_t');
subplot(2,2,4)
plot(y_t);
title('y_t');
图像如下：
“db3”先分解后重构
代码：
clc;clear;
load leleccum;
N=1000;
y = leleccum(1:N);
h=wfilters('db3','l'); % 低通
g=wfilters('db3','h'); % 高通
a1=dyaddown(conv(y,h)); % 2抽取
d1=dyaddown(conv(y,g)); % 2抽取
a2=dyaddown(conv(a1,h)); % 2抽取
d2=dyaddown(conv(a1,g)); % 2抽取
a3=dyaddown(conv(a2,h)); % 2抽取
d3=dyaddown(conv(a2,g)); % 2抽取,
figure(4);
subplot(2,2,1)
plot(a3);
title('a3');
subplot(2,2,2)
plot(d3);
title('d3');
subplot(2,2,3)
plot(d2);
title('d2');
subplot(2,2,4)
plot(d1);
title('d1');
d3_up=dyadup(d3); % 2插值
a3_up=dyadup(a3); % 2插值
d3_up=d3_up(1,[1:N/4]); % 去掉最后一个零
a3_up=a3_up(1,[1:N/4]); % 去掉最后一个零
hr=h(end:-1:1); % 重构低通
gr=g(end:-1:1); % 重构高通
hr=circshift(hr',1)'; % 位置调整圆周右移一位
gr=circshift(gr',1)'; % 位置调整圆周右移一位
a2_t=conv(a3_up,hr)+conv(d3_up,gr);
a2_t=a2_t(1,[3:end]);
a2_up=dyadup(a2_t);
d2_up=dyadup(d2);
d2_up=d2_up(1,[1:N/2]); % 去掉最后一个零
a2_up=a2_up(1,[1:N/2]); % 去掉最后一个零
a1_t=conv(a2_up,hr)+conv(d2_up,gr);
a1_t=a1_t(1,[4:end]);
a1_up=dyadup(a1_t);
d1_up=dyadup(d1);
d1_up=d1_up(1,[1:N]); % 去掉最后一个零
a1_up=a1_up(1,[1:N]); % 去掉最后一个零
y_t=conv(a1_up,hr)+conv(d1_up,gr);
y_t=y_t(1,[6:end]);
figure(6);
subplot(2,2,1)
plot(a2-a2_t);
title('a2-a2_t');
subplot(2,2,2)
plot(a1-a1_t);
title('a1-a1_t');
subplot(2,2,3)
plot(y-y_t);
title('y-y_t');
subplot(2,2,4)
plot(y_t);
title('y_t');
图像如下：
5.3 举例3—分解重构
代码：
clc;clear;
load leleccum;
N=1000;
y = leleccum(1:N);
[c,l]=wavedec(y,3,'db1');
y1 = waverec(c,l,'db1');
[c,l]=wavedec(y,3,'db3');
y3 = waverec(c,l,'db1');
figure(7);
subplot(2,3,1)
plot(y);
title('y');
subplot(2,3,2)
plot(y1);
title('y1');
subplot(2,3,3)
plot(y3);
title('y3');
subplot(2,3,5)
plot(y-y1);
title('y-y1');
subplot(2,3,6)
plot(y-y3);
title('y-y3');
图像：
综上所述笔者认为“db3”效果偏差
参考文献：
- 形象易懂讲解算法I——小波变换
- 一起学小波
- wavedec