python库实现线性回归_怎样用Python的Scikit-Learn库实现线性回归？

回归和分类是两种 监督 机器 学习算法， 前者预测连续值输出，而后者预测离散输出。 例如，用美元预测房屋的价格是回归问题，而预测肿瘤是恶性的还是良性的则是分类问题。

在本文中，我们将简要研究线性回归是什么，以及如何使用Scikit-Learn(最流行的Python机器学习库之一)在两个变量和多个变量的情况下实现线性回归。

线性回归理论

代数学中，术语“线性”是指两个或多个变量之间的线性关系。 如果在二维空间中绘制两个变量之间的关系，可以得到一条直线。

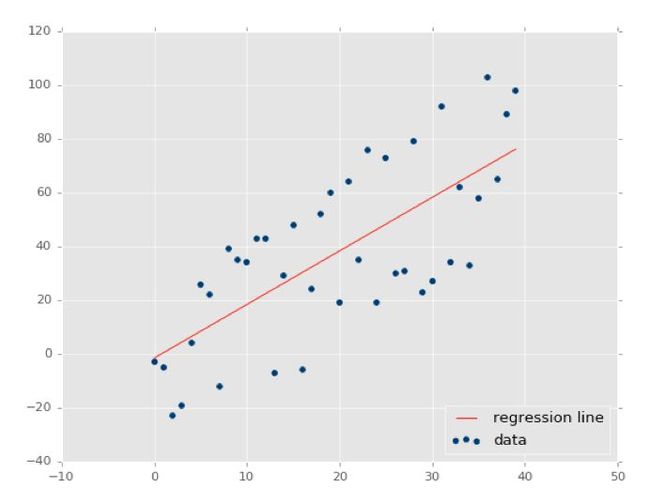
线性回归可以根据给定的自变量(x)预测因变量值(y)，而这种回归技术可以确定x(输入)和y(输出)之间的线性关系，因此称之为线性回归。 如果在x轴上绘制自变量(x)，又在y轴上绘制因变量(y)，线性回归给出了一条最符合数据点的直线，如下图所示。

得出线性方程大概是：

上述等式应为： Y= mx + b

其中b是截距，m是直线的斜率。 线性回归算法大体上提供了截距和斜率的最优值。 因为x和y是数据特征，因此这两个变量保持不变。 可以控制的值是截距(b)和斜率(m)。 根据截距和斜率的值，图上可以有多条直线。 线性回归算法的可以找到符合数据点的多条线，并确认导致最小误差的其中一条线。

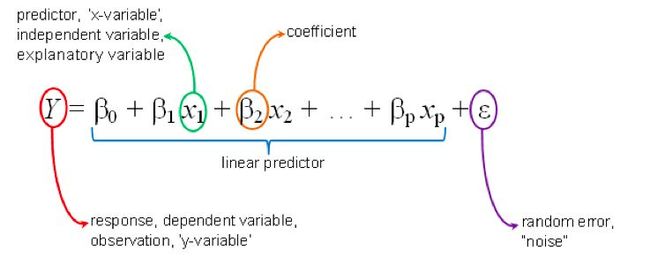
两个以上的变量的情况也适合使用线性回归，这可称为多元线性回归。 比方说，假设这样一个场景，你必须根据房屋面积、卧室数量、住房人口的平均收入、屋龄等来预测房屋的价格。 在这种情况下，因变量(目标变量)取决于几个不同的独立变量。 而这种涉及多个变量的回归模型可表示为：

y = b0 + m1b1 +m2b2 + m3b3 + ... mnbn

这是超平面的等式。 请牢记，二维线性回归模型是一条直线; 而三维线性回归模型则是一个平面，并且三维以上是超平面。

本节内容将介绍Python中用于机器学习的Scikit-Learn库如何实现回归函数。 我们将从涉及两个变量的简单线性回归开始，然后逐步转向涉及多个变量的线性回归。

简单线性回归

线性回归

在查看第二次世界大战数据集中空中轰炸行动的记录时，我发现恶劣天气几乎要推迟当时的诺曼底登陆，下载了当时的天气报告，以便与轰炸行动数据集的任务进行比较。

该数据集包含世界各地气象站每天记录的天气状况信息，内容包括降水、降雪、气温和风速，同时也记录了当天是否出现雷暴或其他恶劣天气情况。

将这些输入特征值看成是最低温度，从而以预测最高温。

开始编码

导入所需的库：

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

import seaborn as seabornInstance

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn import metrics

%matplotlib inline

以下命令使用pandas导入CSV数据集：

dataset =pd.read_csv('/Users/nageshsinghchauhan/Documents/projects/ML/ML_BLOG_LInearRegression/Weather.csv')

通过检查数据集内的行数和列数，大概对数据有了一点认识。

dataset.shape

如果输出值写着 (119040, 31)，这意味着这个数据集含有119040行和31列。

可以使用describe()以查看数据集的统计详细信息：

dataset.describe()

数据集的统计视图

最后，在二维图上绘制我们的数据点并观察我们的数据集，看看是否可以使用以下脚本手动查找数据之间的关系：

dataset.plot(x='MinTemp', y='MaxTemp',)

plt.title('MinTemp vs MaxTemp')

plt.xlabel('MinTemp')

plt.ylabel('MaxTemp')

plt.show()

我们采用了MinTemp和MaxTemp进行分析。 下面是MinTemp和MaxTemp之间的二维图。

查找一下平均最高温度——二维图绘制完成后，可以观察到平均最高温度在25(摄氏度)和35(摄氏度)之间。

plt.figure(figsize=(15,10))

plt.tight_layout()

seabornInstance.distplot(dataset['MaxTemp'])

平均最高温在20到35之间

下一步，把这些数据分为“属性”和“标签”两类。

属性是自变量，而标签是因变量，其值有待预测。 在我们的数据集中，我们只有两列数据。 我们想根据记录的MinTemp来预测MaxTemp，因此属性集将包含存储在X变量中的“MinTemp”列，而标签则存储在y变量中的“MaxTemp”列。

X = dataset['MinTemp'].values.reshape(-1,1)

y = dataset['MaxTemp'].values.reshape(-1,1)

接下来，80%的数据将作为训练样本集，而另外的20%则用于测试以下编码。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=0)

在将数据分成训练集和测试集后，便开始训练算法。 为此，需要导入LinearRegression类，并将之实例化，并采用fit()方法已验证这些训练数据。

regressor = LinearRegression()

regressor.fit(X_train, y_train) #training the algorithm

我们前面曾讨论过，线性回归模型可以大致找到截距和斜率的最佳值，从而确定最符合相关数据的线的位置。如要查看线性回归算法为我们的数据集计算的截距和斜率的值，请执行以下代码。

#To retrieve the intercept:

print(regressor.intercept_)

#For retrieving the slope:

print(regressor.coef_)

结果分别约为10.66185201与0.92033997。

这意味着——若最低温度发生变化，那么最高温度有0.92%的可能性也发生变化。

既然已经训练了这算法，现在是时候进行一些预测了。 为需要测试数据，并检验算法预测百分比得分的准确程度。 要对测试数据进行预测，请执行以下脚本：

y_pred = regressor.predict(X_test)

现在将X_test的实际输出值与预测值进行比较，请执行以下脚本：

df = pd.DataFrame({'Actual': y_test.flatten(), 'Predicted':y_pred.flatten()})

df

实际值与预测值的比较

还可以使用以下脚本，用条形图的方式展示这些比较：

注意： 由于记录数量庞大，为了更好的展示效果，我们只使用了其中25条记录。

df1 = df.head(25)

df1.plot(kind='bar',figsize=(16,10))

plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')

plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')

plt.show()

实际值与预测值比较的条形图

尽管这个模型不尽准确，但预测的百分比依然接近实际数值。

根据这些测试数据可以画出一条直线：

plt.scatter(X_test, y_test, color='gray')

plt.plot(X_test, y_pred, color='red', linewidth=2)

plt.show()

预测值和测试数据

图上直线显示我们的算法无误。

最后一步是评估算法的性能。 此步骤对于比较不同算法在特定数据集上的实现情况尤为重要。 对于回归算法，通常使用三种评估指标：

1.平均绝对误差(MAE)指的是误差绝对值的平均值。 计算方法如下：

2.均方误差(MSE)是平方误差的平均值，计算公式如下：

3.均方根误差 (RMSE)为平方误差均值的平方根：

幸运的是，我们无需手动计算，Scikit-Learn库的预建功能可以计算这些值。

使用测试数据找到这些指标的值。

print('MeanAbsolute Error:', metrics.mean_absolute_error(y_test, y_pred))

print('MeanSquared Error:', metrics.mean_squared_error(y_test, y_pred))

print('RootMean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred))

你会得到这样的输出结果(结果可能略有不同)：

('MeanAbsolute Error:', 3.19932917837853)

('MeanSquared Error:', 17.631568097568447)

('RootMean Squared Error:', 4.198996082109204)

由上可见，均方根误差的值是4.19，这个数值超过了所有温度百分比平均值的10％，即22.41。 这意味着我们的算法不是很准确，但预测能力良好。

多元线性回归

来源

上面部分主要针对两个变量进行线性回归，但你遇到的所有实际问题中变量可不止两个。 涉及多个变量的线性回归则称为“多元线性回归”。 执行多元线性回归的步骤与简单线性回归的步骤相似。 不同之处在于评估过程。 利用多元线性回归可以找出哪个因素对预测输出的影响最大，以及不同变量之间的相互关系。

在本节中，我们下载了红葡萄酒质量数据集，该数据集与葡萄牙的“Vinho Verde”(绿酒)葡萄酒的红色变体有关。 由于隐私和后勤问题，我们只掌握物理化学(输入)变量和感官(输出)变量的数据(例如，关于葡萄类型，葡萄酒品牌，葡萄酒销售价格等的数据暂缺)。

将考虑各种输入特征，如固定酸度，挥发性酸度，柠檬酸，残糖，氯化物，游离二氧化硫，总二氧化硫，密度，pH，硫酸盐，酒精。 我们将利用这些特征来预测葡萄酒的质量。

开始编码

输入所需的库：

importpandas as pd

importnumpy as np

importmatplotlib.pyplot as plt

importseaborn as seabornInstance

fromsklearn.model_selection import train_test_split

fromsklearn.linear_model import LinearRegression

fromsklearn import metrics

%matplotlibinline

以下指令将通过上面的链接从下载的文件中导入数据集：

dataset =pd.read_csv('/Users/nageshsinghchauhan/Documents/projects/ML/ML_BLOG_LInearRegression/winequality.csv')

通过检查数据集内的行数和列数，我们大概对以上数据有了一点认识。

dataset.shape

若输出值为(1599,12)，则表明数据集中行数为1599，列数为12.

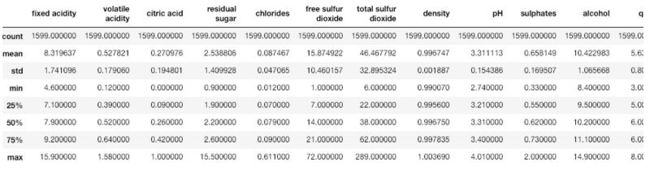
我们可以使用describe()以查看数据集的统计详细信息：

dataset.describe()

我们还需对数据进行筛选，首先查找哪些列含有NaN值：

dataset.isnull().any()

执行上面的代码后，所有列都会显示最后的结果False，如果有一列出现了True，则使用下面的代码从该列中删除所有空值。

dataset= dataset.fillna(method='ffill')

下一步是将数据划分为“属性”和“标签”。 X变量包含所有属性/特征，y变量包含标签。

X = dataset[['fixed acidity', 'volatileacidity', 'citric acid', 'residual sugar', 'chlorides', 'free sulfur dioxide','total sulfur dioxide', 'density', 'pH', 'sulphates','alcohol']].values

y = dataset['quality'].values

计算“质量”一行的平均值。

plt.figure(figsize=(15,10))

plt.tight_layout()

seabornInstance.distplot(dataset['quality'])

葡萄酒质量的平均值

从上图可得，大部分葡萄酒的质量平均值为5或6。

接下来，80%的数据将作为训练样本集，而另外的20%则用于测试以下编码。

X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

现在开始测试模型。

regressor= LinearRegression()

regressor.fit(X_train,y_train)

如前所述，在多变量线性回归中，回归模型必须找到所有属性的最佳系数。 如要查看该回归模型选择了哪些系数，请执行以下脚本：

coeff_df= pd.DataFrame(regressor.coef_, X.columns, columns=['Coefficient'])

coeff_df

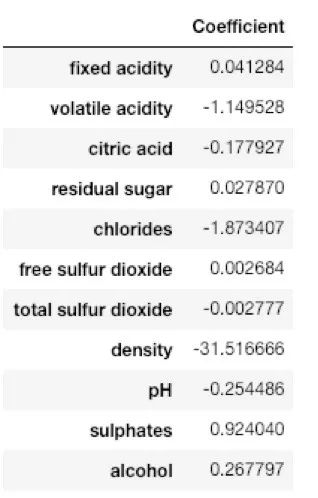
最后的输出值大致如下：

这意味着，随着“密度”的单位增加，葡萄酒的质量减少了31.51个单位。 同理，“氯化物”的单位的减少也会使得葡萄酒质量增加1.87个单位。 同时我们还可以可以看到其余的特征对葡萄酒的质量影响很小。

现在对测试数据进行预测。

y_pred= regressor.predict(X_test)

检验实际值和预测值之间的差异。

df =pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})

df1= df.head(25)

实际值与预测值的对比

对实际值和预测值之间对比进行描点：

df1.plot(kind='bar',figsize=(10,8))

plt.grid(which='major',linestyle='-', linewidth='0.5', color='green')

plt.grid(which='minor',linestyle=':', linewidth='0.5', color='black')

plt.show()

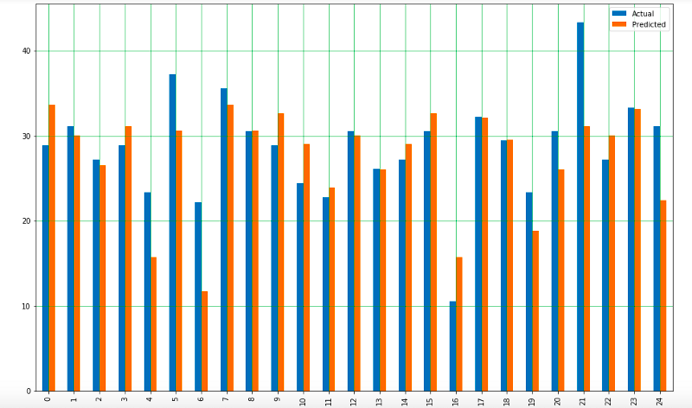
以上条形图可用于展示预测值和实际值之间的差异

可以看到，这个模型的预测结果比较准确。

最后一步是评估算法的性能。 我们将通过计算MAE，MSE和RMSE的值来完成此操作。 请执行以下脚本：

print('MeanAbsolute Error:', metrics.mean_absolute_error(y_test, y_pred))

print('MeanSquared Error:', metrics.mean_squared_error(y_test, y_pred))

print('RootMean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

输出值为：

('MeanAbsolute Error:', 0.46963309286611077)

('MeanSquared Error:', 0.38447119782012446)

('RootMean Squared Error:', 0.6200574149384268)

可以看到，均方根误差值为0.62，略大于所有状态下的气体消耗平均值的10％，即5.63。 这意味着算法还不够精准，但其预测能力依然让人认同。

导致这种不准确的有多种因素，如：

· 数 据量不足 ： 需要大量数据才能获得最准确的预测。

· 假设失误 ： 假设这些数据具有线性关系，但实际可能并非如此。 可以将数据可视化来确定结果。

· 属性关联度低 ： 参与计算的属性与我们的预测值关联度不大。