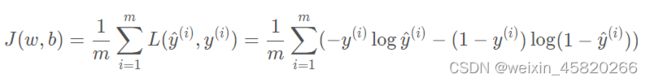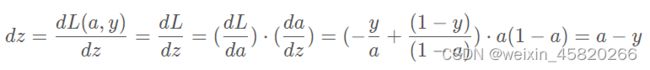Titanic(Kaggle)-Logistic（2）

目录

Logistic简介

Logistic回归和线性回归的区别

损失函数

梯度下降GD

计算图

向量化

完整代码

pytorch版本

总结

---

Logistic简介

Logistic是一种广义的线性回归，主要是用来处理二分类问题。

对于二分类问题，输入一个特征向量x，x表示数据集中的一个样本，它是一个（1,7）的向量，所以用w表示参数，w就是一个（7*1）的向量；b是偏置，本文在做题的时候没有考虑偏置问题，加b的时候会有一个python中的广播机制。y是标签（表示是否生存，0否1是），h是线性回归的输出. h= x*w，至此得到了线性回归的输出，然后把这个输出输入到一个激活函数sigmoid中得到一个大于0的概率值。

Logistic回归和线性回归的区别

线性回归的因变量是连续性数值，而Logistic回归的因变量是分类型变量；

线性回归是直接观察因变量和自变量之间的关系，Logistic回归时观察因变量概率和自变量的关系.

---

损失函数

想要让损失函数尽可以能小，可以看到选择交叉熵函数作为损失函数，当y=1，L=-log(y_hat)；当y=0，L=-log(1-y_hat)。

交叉熵：L(y_hat, y) = -ylog(y_hat）- （1-y）log(1-y_hat)；

对于m个样本来说，成分函数（代价函数）

 我在做题中也尝试了用均方误差作为损失函数进行了实验。就是预测值和实际值查的平方的平均值。

---

梯度下降GD

本质上就是通过最小化成本函数J来训练参数w；有7个特征，每次都朝最陡的下坡方向走一步，不断迭代。学习率就是来控制每次走的步长，每次走的长度就是dJ/dw的求导 .其实梯度下降就是反向传播的过程，最终得到最优的参数w，让模型能够完成任务。

Logistic回归用到的公式：

 

 

---

计算图

计算图其实就是将前向传播和反向传播显示表达出来，从左到右是前向传播计算预测值和成本的过程，从右到左是不断更新参数，不断求导使得成本降低的过程。

---

向量化

向量化可以加速代码，由于向量化主要可以避免显示的for循环，充分利用并行化计算。

对于Titanic一共有981个（训练）样本，所以，数据集可以表示为X（981,7）的矩阵，y表示是否生存（981,1），w是（7,1）。那么，H = X*w得到一个（891， 1）的输出，再将H输入到sigmoid函数中，得到y_hat也是（981,1）。最后将y和y_hat进行比较可以得到模型的训练准确率。

完整代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

train_df = pd.read_csv("data/train_pre.csv")
test_df = pd.read_csv("data/test_pre.csv")

X_train = train_df.drop(['Survived', 'PassengerId'], axis=1)
Y_train = train_df["Survived"]
X_test = test_df.drop(['PassengerId'], axis=1)
samples_size, feature_size = X_train.shape[0], X_train.shape[1]


def linreg(X, w):
    return np.dot(X, w)


def sigmoid(h):
    return 1 / (1+np.exp(-h))


def sgd(x, y, w, lr=0.01, num_epochs=5000):
    y = np.mat(y).transpose()
    costs = []
    for epoch in range(num_epochs):
        # 前向
        h = linreg(x, w)
        y_hat = sigmoid(h)
        cost = (- 1 / samples_size) * np.sum(y.transpose() * np.log(y_hat) + (1 - y).transpose() * (np.log(1 - y_hat)))  # 计算成本
        cost = np.squeeze(cost)

        # 后向
        dz = (y_hat - y)
        dw = (np.dot(x.transpose(), dz)) / samples_size
        w = w - lr * dw

        costs.append(cost)
        if epoch % 100 == 0:
            costs.append(cost)
            print("迭代的次数: %i ， 误差值： %f" % (epoch, cost))

    return w, costs


def predict(w, X):
    Y_pred = np.zeros((1, samples_size))
    y_hat = sigmoid(linreg(X, w))
    for i in range(y_hat.shape[0]):
        if y_hat[i, 0] > 0.5:
            Y_pred[0, i] = 1
    return Y_pred


w = np.ones((feature_size, 1))
w, costs = sgd(X_train, Y_train, w)

print(w)
plt.plot(costs)
plt.title("training loss")
plt.show()


Y_pred = predict(w, X_train)
print("训练集准确性：", format(100 - np.mean(np.abs(Y_pred - np.mat(Y_train).transpose())) * 100), "%")

pytorch版本

import torch
import pandas as pd
import numpy as np

train_df = pd.read_csv("data/train_pre.csv")
test_df = pd.read_csv("data/test_pre.csv")

X_train = train_df.drop(['Survived', 'PassengerId'], axis=1)
Y_train = train_df["Survived"]
X_test = test_df.drop(['PassengerId'], axis=1)

X_train = torch.from_numpy(X_train.to_numpy()).float()
Y_train = torch.from_numpy(Y_train.to_numpy()).float()
X_test = torch.from_numpy(X_test.to_numpy())
samples_size, feature_size = X_train.shape[0], X_train.shape[1]


class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear = torch.nn.Linear(7, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        y_pred = self.sigmoid(self.linear(x))
        return y_pred


model = Model()

loss = torch.nn.BCELoss(reduction='mean')
opt = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(500):
    y_pred = model(X_train)

    l = loss(y_pred, Y_train)
    if epoch % 100 == 0:
        print(f'epoch {epoch}, loss {l}')

    opt.zero_grad()
    l.backward()
    opt.step()


for i in model.parameters():
    print(i)

for i in range(y_pred.shape[0]):
    y_pred[i, 0] = 1 if y_pred[i, 0] > 0.5 else 0

y_pred = y_pred.detach().numpy()

print("训练集准确性：", format(100 - np.mean(np.abs(y_pred - np.mat(Y_train).transpose())) * 100), "%")

总结

通过本次实验，用Logistic回归对处理过的Titanic数据进行训练预测，熟悉了Logistic的原理，并且用pytorch编写的时候通过构造网络，对神经网络有了一个基本的了解；熟悉了前向传播和反向传播的过程。在学习的过程中，观看了吴恩达老师的课程，也有了很多的启发。在编码的过程中，对于矩阵的计算，先搞明白矩阵的形状是最重要的。除了上述代码，我还调用了库函数，最后实验结果库函数的结果最优，准确率达到80%，使用pytorch版本达到75%，而基础版本的准确率只有50%多。