陪审团题解

状 态 表 示 : f [ i ] [ j ] [ k ] : 从 前 i 个 人 中 挑 选 了 j 个 人 , 且 对 应 的 辩 方 总 分 和 控 方 总 分 的 差 值 为 k , 的 最 大 总 分 状态表示:f[i][j][k]:从前i个人中挑选了j个人,且对应的辩方总分和控方总分的差值为k,的最大总分 状态表示:f[i][j][k]:从前i个人中挑选了j个人,且对应的辩方总分和控方总分的差值为k,的最大总分
状 态 转 移 方 程 : 状态转移方程: 状态转移方程:
f [ i , j , k ] = { f [ i − 1 ] [ j ] [ k ] ( 不 选 择 i ) f [ i − 1 , j − 1 , k − ( d [ i ] − p [ i ] ) ] ( 选 择 了 i ) f[i,j,k]=\left\{ \begin{matrix} f[i-1][j][k](不选择i) \\ f[i-1,j-1,k-(d[i]-p[i])](选择了i) \end{matrix} \right. f[i,j,k]={f[i−1][j][k](不选择i)f[i−1,j−1,k−(d[i]−p[i])](选择了i)
**容易错的点:**预处理的时候要把所有 j = = 1 j==1 j==1的情况处理出来,这种情况比较好处理。
**为什么需要单独处理?**比如下图
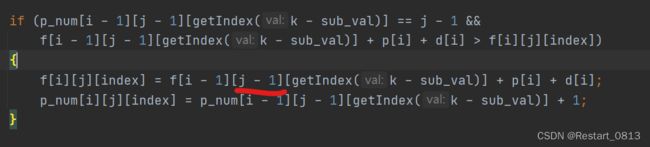
我 们 在 进 行 d p 的 时 候 , 要 访 问 到 我们在进行dp的时候,要访问到 我们在进行dp的时候,要访问到j-1 , 也 就 是 0 是 有 可 能 被 访 问 的 , 但 是 选 择 0 个 是 没 被 定 义 的 , 因 此 需 要 单 独 处 理 。 ,也就是0是有可能被访问的,但是选择0个是没被定义的,因此需要单独处理。 ,也就是0是有可能被访问的,但是选择0个是没被定义的,因此需要单独处理。
我 们 还 需 要 考 虑 是 否 能 够 进 行 f [ i , j , k ] = f [ i − 1 , j , k ] 什 么 时 候 不 能 进 行 这 步 呢 ? 当 根 本 无 法 从 前 i − 1 个 人 中 无 法 取 出 j 个 人 的 时 候 我们还需要考虑是否能够进行f[i,j,k]=f[i-1,j,k] 什么时候不能进行这步呢?\\ 当根本无法从前i-1个人中无法取出j个人的时候 我们还需要考虑是否能够进行f[i,j,k]=f[i−1,j,k]什么时候不能进行这步呢?当根本无法从前i−1个人中无法取出j个人的时候
因此我们需要增加一个p_num数组保存每一步的dp都取了多少个人
遍历公差的时候,还要判断是否这个人能够添加进去,也就是k-sub_val是否合法
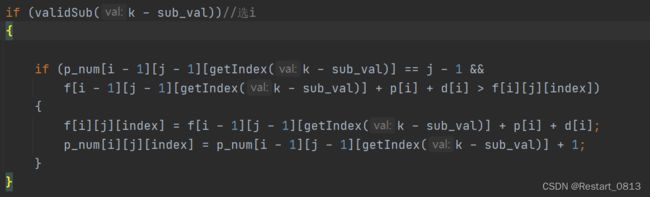
最 后 找 到 解 决 方 案 : 我 们 先 看 一 下 递 推 的 公 式 最后找到解决方案:我们先看一下递推的公式 最后找到解决方案:我们先看一下递推的公式
f [ i , j , k ] = { f [ i − 1 , j , k ] ( 选 择 了 i ) f [ i − 1 , j − 1 , k − ( d [ i ] − p [ i ] ) ] + p [ i ] + d [ i ] ( 没 有 选 择 i ) f[i,j,k]=\left\{\begin {matrix} f[i-1,j,k](选择了i) \\ f[i-1,j-1,k-(d[i]-p[i])]+p[i]+d[i](没有选择i) \end{matrix} \right. f[i,j,k]={f[i−1,j,k](选择了i)f[i−1,j−1,k−(d[i]−p[i])]+p[i]+d[i](没有选择i)
如 果 f [ n , m , f i n a l k ] ! = f [ n , m , f i n a l k ] , 说 明 了 取 到 了 第 n 个 如果f[n,m,final_k]!=f[n,m,final _ k],说明了取到了第n个 如果f[n,m,finalk]!=f[n,m,finalk],说明了取到了第n个
因 此 我 们 倒 过 来 遍 历 就 行 , 注 意 k 和 j 的 更 新 因此我们倒过来遍历就行,注意k和j的更新 因此我们倒过来遍历就行,注意k和j的更新
对 了 , 在 初 始 化 数 组 的 时 候 , 不 要 和 合 法 的 数 组 值 冲 突 , 否 则 很 难 辨 认 。 比 如 最 后 一 次 提 交 的 时 候 我 w a 了 一 发 , 因 为 我 把 其 中 两 个 数 组 初 始 化 为 0 , 在 输 入 的 值 为 全 0 的 时 候 就 会 错 误 , 改 成 m e m s e t − 1 就 好 了 对了,在初始化数组的时候,不要和合法的数组值冲突,否则很难辨认。\\比如最后一次提交的时候我wa了一发,因为我把其中两个数组初始化为0\\,在输入的值为全0的时候就会错误,改成memset -1 就好了 对了,在初始化数组的时候,不要和合法的数组值冲突,否则很难辨认。比如最后一次提交的时候我wa了一发,因为我把其中两个数组初始化为0,在输入的值为全0的时候就会错误,改成memset−1就好了
#include