【数据结构与算法】粽子树？二叉树_关于堆你不知道事情

前情提要

本章节是数据结构的堆的相关知识~

接下来我们即将进入一个全新的空间，对代码有一个全新的视角~

以下的内容一定会让你对数据结构有一个颠覆性的认识哦！！！

❗以下内容以C语言的方式实现，对于数据结构来说最重要的是思想哦❗

以下内容干货满满，跟上步伐吧~

---

作者介绍：

作者： 热爱编程不起眼的小人物
作者的Gitee：代码仓库
系列文章&专栏推荐： 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》

我和大家一样都是初次踏入这个美妙的“元”宇宙 希望在输出知识的同时，也能与大家共同进步、无限进步

---

---

本章重点

• 堆的概念

• 堆的结构&实现

• 向上调整&向下调整重要算法思想

---

一.堆的概念

Ⅰ.什么是堆

• 堆总是一颗完全二叉树【满二叉树为特殊的完全二叉树】

• 堆又称为二叉树的顺序结构

  • 因为普通的二叉树不适合用数组来存储，可能会造成大量的空间浪费

  • 而完全二叉树用顺序结构存储是完全嵌合的，不会存在空间浪费

❗综上：

• 堆的逻辑结构为完全二叉树

• 堆的物理结构为数组

Ⅱ.总结

✨综上：就是堆的概念啦~

➡️简单来说：堆为二叉树的顺序结构

【后续我们还会学习二叉树的链式结构哦~】

---

二.堆

Ⅰ.性质

在堆中： 某个节点的值总是不大于或不小于其父节点的值

• 大根堆：即当每个父亲结点的值总是≥孩子结点的值

• 小根堆：即当每个父亲结点的值总是≤孩子结点的值

❗特别注意：

• 小根堆的堆顶数据【即最上面的结点的值】：一定是整个完全二叉树中值最小的结点

• 大根堆的堆顶数据【即最上面的结点的值】：一定是整个完全二叉树中值最大的结点

• 若不满足上述条件，则表明不属于大根堆或小根堆中的任意一个，也就是说此完全二叉树不是堆

【虽然根结点的值一定是全部结点的值中最大或最小的，但大根堆、小根堆并不代表说数组元素是按照降序、升序排放的，这两者没有任何关系】

➡️重要规律：

通过数组的特性随机访问，如何用下标去找到父亲结点or孩子结点

• 假设某一个父亲结点下标为parent

• 所以此父亲结点的左孩子结点为：leftchild = parent*2 + 1

• 所以此父亲结点的右孩子结点为：leftchild = parent*2 + 2

• 所以：我们可以通过+1、+2的下标调整找到左孩子、右孩子

• 那此时我们就可以反推出：parent = （child - 1）/ 2

• 这是因为计算的是整型计算，即使是右孩子去用此算式虽然计算出来的下标是带有小数的，但下标的类型为整型，就会自动抹去小数，那此时的整数也就为右孩子的父亲结点的下标了

• 所以：我们就可以用一条算式去求得左、右孩子的父亲结点的下标了，无需用两条算式

✨综上：

• 我们便用顺序结构去实现堆

❗所以下面我们开始实现堆的接口

---

三.堆接口实现

对于数据结构的接口实现，一般围绕增、删、查、改的内容

如下的实现围绕此原码进行： 以下以建大根堆为例

typedef int HPDataYtpe;

typedef struct Heap
{
	HPDataYtpe *a;
	int size; //记录目前数组内有几个数据
	int capacity;
	
}HP;

Ⅰ.初始化堆（建堆）

简单来说：

• 拿一个数组的全部元素进行建堆，即对此数组的逻辑结构变为大堆

➡️实现：

• 1️⃣先将原先数组的内容全部拷贝至新创建的堆中

• 2️⃣将此堆里的元素排序进行调整，建为 大堆

重点： 如何调整为大堆 - 也就是建堆

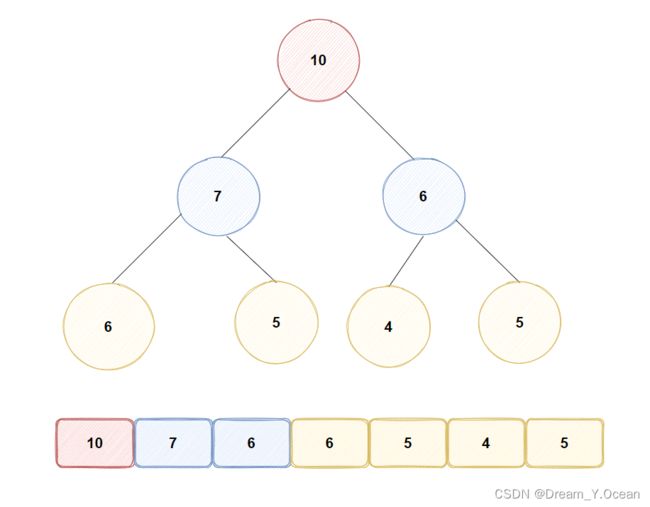
1.首先：我们假设要建堆的数组的元素除了根节点不满足大堆，左右子树都满足大堆的情况

---

2.思路：此时我们就需要将值为2的结点进行向下比较，最终放到适合的位置，从而使整个堆满足大堆的要求

向下调整算法： 当左右子树都为大堆或小堆的时候，便可通过此算法调整根结点的位置，使整棵树满足大堆或小堆【我们这里本质操控的是数组】

• 1️⃣先将值为2的结点（父亲结点）的左、右孩子比较值的大小，因为是要建大堆，所以选出左右孩子中的较大值

• 2️⃣比较父亲结点与左右孩子中的较大值哪个值更大，若孩子节点的值大于父亲节点，则交换调整，并将原来孩子的位置当成父亲（因为前面已经交换位置了），继续重复调整下去，直至父亲结点走到叶子结点，说明父亲结点已经走到树的最后一层，完成调整了

• 3️⃣若当孩子结点的值小于父亲结点，说明此时父亲结点处在的位置再往下已经满足大堆的要求，就可以停止调整了
  

---

❗特别注意：

• 比较孩子结点的时候，有可能只有左孩子结点，没有右孩子结点的时候（就如上述情况），不可访问右孩子结点，即需要防止数组越界【child + 1 < n】

✊综上：向下调整算法的代码实现【时间复杂度：$O(logN)$】

void ADjustDown(int * a, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child < n) 
	//当 孩子的下标 超出 数组的范围，则说明不存在
	{
		//1.选出左右孩子中，较小的一个
		//child -- 左孩子下标；child+1 -- 右孩子下标
		if (child + 1 < n && a[child + 1] > a[child])
		{
			//想象的时候：默认左孩子是比右孩子小
			//如果大的话，child就走到右孩子下标处
			child++;
		}

		//2.交换
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			//满足的情况
			break;
		}
	}
}

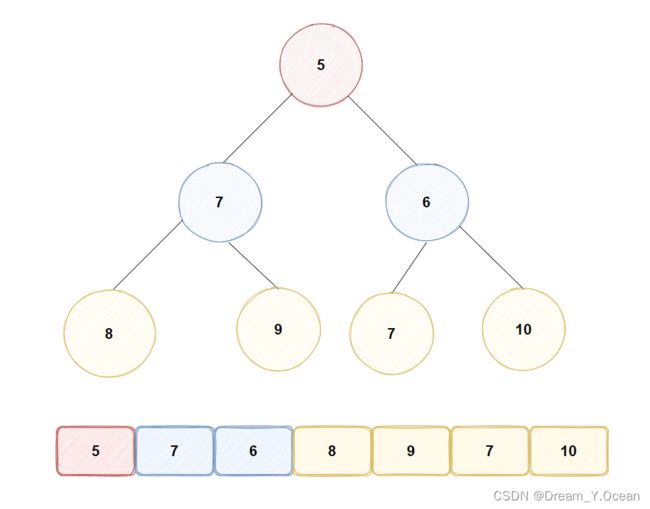
❓当左右子树都不是大堆时候，怎么办

• 上述仅用于左右子树都满足 大堆或小堆的情况，我们现在对于一个结点数值都是随机摆放的完全二叉树，是不能直接运用向下调整算法进行建堆的

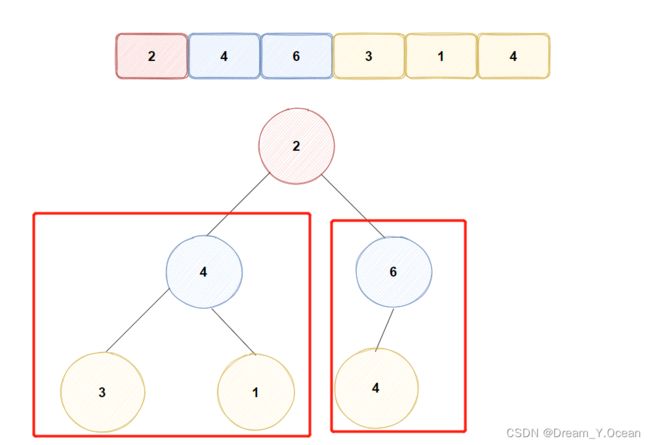
• 那此时我们便可以创造条件：从后往前建堆

➡️思路：

• 1️⃣找到完全二叉树中最后一个结点的父亲结点

• 2️⃣判断此父亲结点与其孩子结点构成的局部二叉树是否是我们想要的大堆，若不满足，则向下调整使这个局部的二叉树满足

• 3️⃣调整完后，父亲结点对应的下标--【即往前找上一个结点】，再重复步骤2️⃣，直至调整为我们上面举的例子，最终调整最后一次后，这个完全二叉树便为大堆
  
  
  
  这样，便正真建成了一个大堆

✊综上：建堆的代码实现【时间复杂度：$O(N)$】

for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
	AdjustDown(php->a, php->size, i);
}

❗特别注意：

• a表示需要建堆的数组的首元素地址

• n为数组的a的元素个数

1️⃣建堆的函数声明：

void HeapInit(HP* php,HPDataYtpe* a,int n);

2️⃣建堆函数的实现：

void HeapInit(HP* php, HPDataYtpe* a, int n)
{
	assert(php);

	php->a = (HPDataYtpe*)malloc(sizeof(HPDataYtpe)*n);
	if (php->a == NULL)
	{
		printf("malloc fail\n");

		exit(-1);
	}
	
	//1.拷贝
	memcpy(php->a, a, sizeof(HPDataYtpe)*n);
	php->size = n;
	php->capacity = n;

	//2.建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(php->a, php->size, i);
	}
}

Ⅱ.入堆操作

简单来说： 对堆插入一个数据

➡️实现： 即对数组尾插一个数据

❗特别注意：

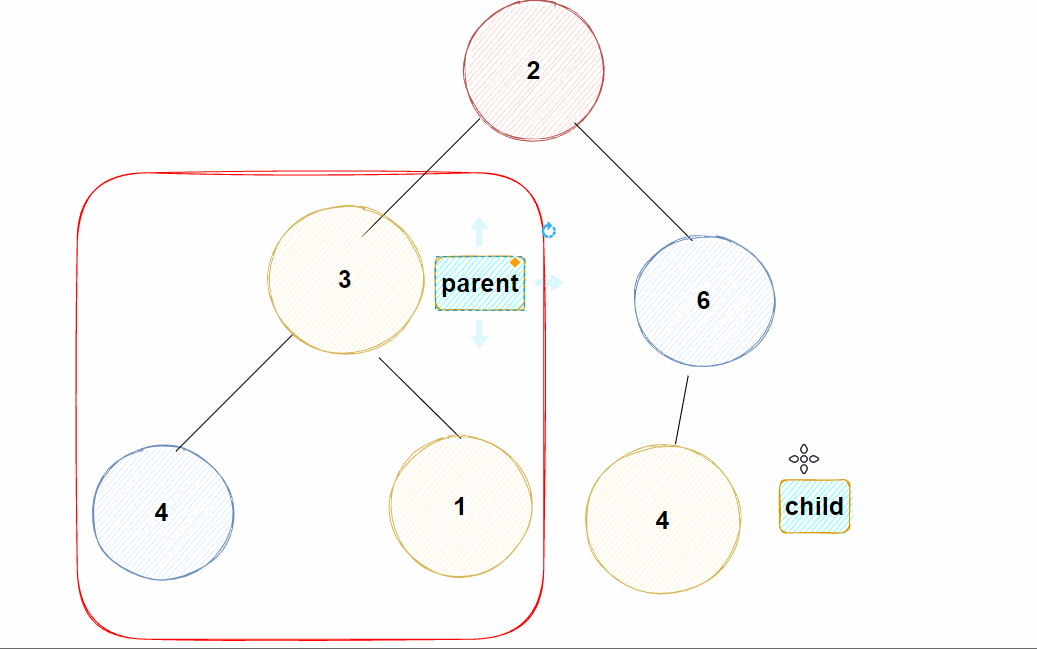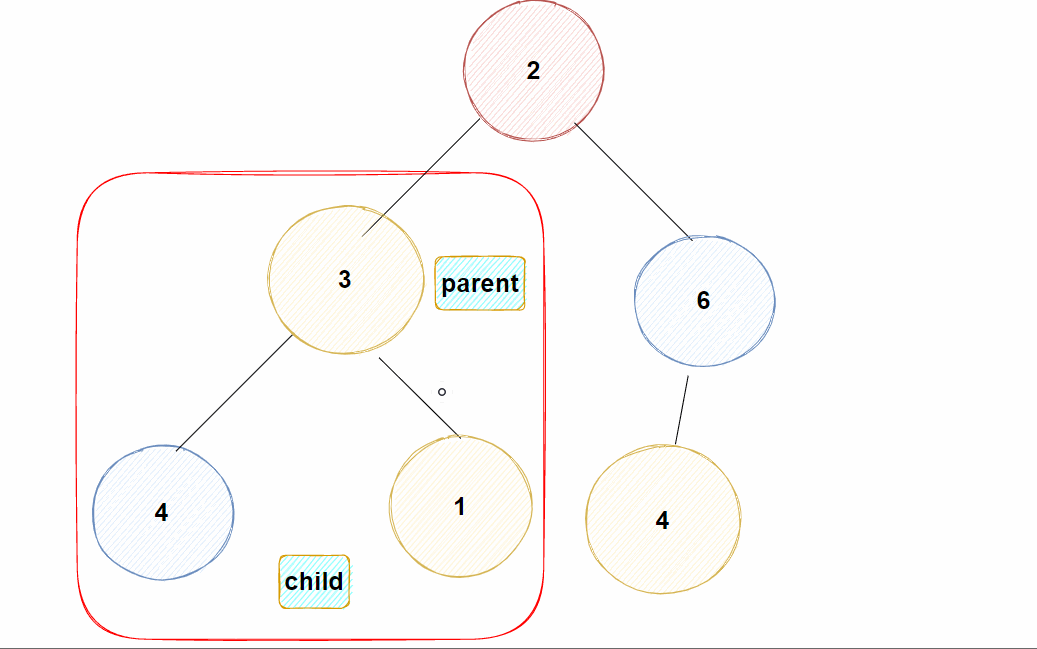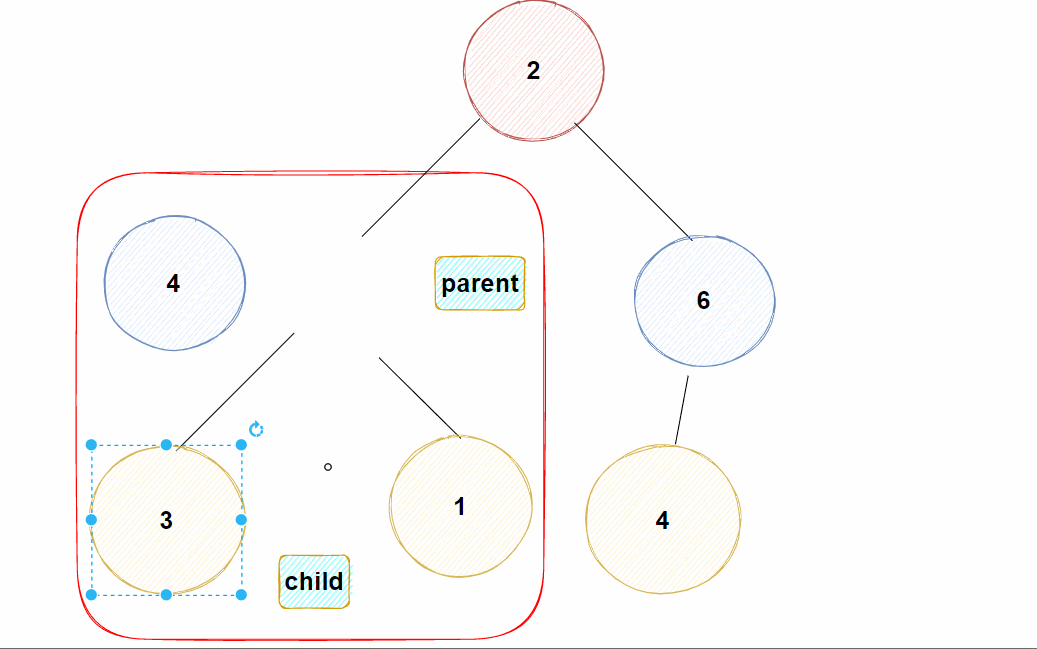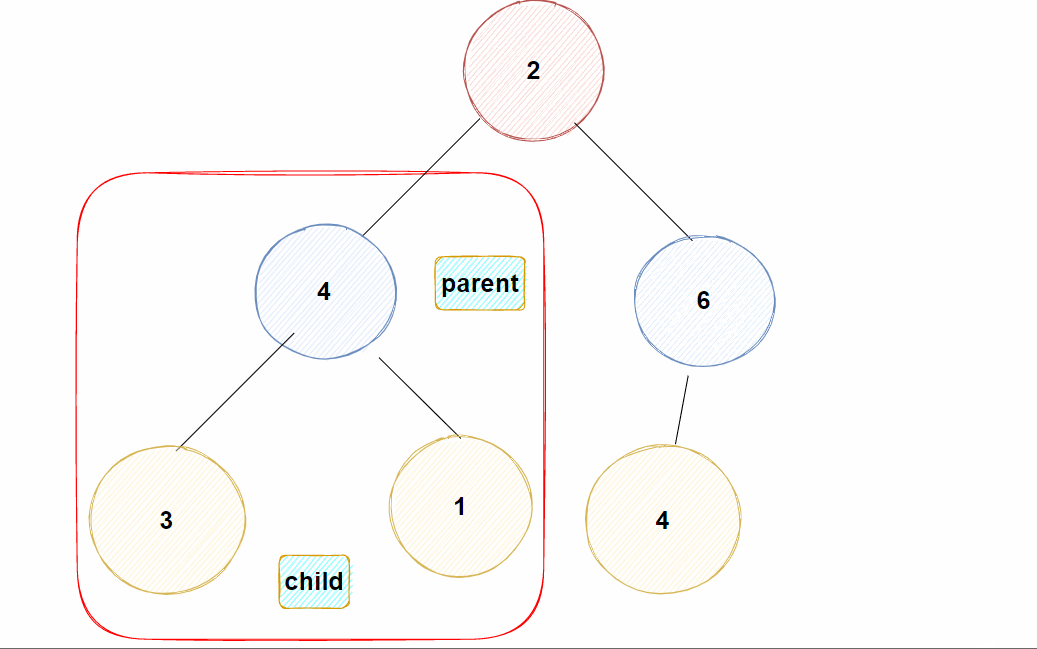
• 并不是插入堆就直接满足大堆，需要将刚插进来的数据经过比较放到能使整棵树满足大堆的位置，此时就涉及另外一个算法：向上调整算法

  • 对插入的数据进行向上调整，仅会对插入数据所在的路径产生影响，并不像向下调整算法会影响到整棵树

  • 因为我们插入进来的时候，完全二叉树已经满足大堆【即父亲结点的值≥孩子结点的值】，所以向上调整算法将插入的结点直接与父亲结点的值进行比较即可（无需与自己的兄弟结点比较）

    • 若大于父亲结点的值，则不满足大堆，需要将插入进来的结点与其父亲结点交换，并继续向上与新的父亲结点进行比较

    • 直至插入的结点已经到达根部【即数组下标为0处】 ，就结束调整，表示已到达合适的位置

    • 若小于父亲结点的值，则表明此时也已满足大堆，插入进来的结点已经到达合适的位置了

✊综上：向上调整代码实现

void Adjustup(int*a, int child)
{
	int parent = (child - 1) / 2;
	while (child = 0)  //等于0的时候就中止 
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

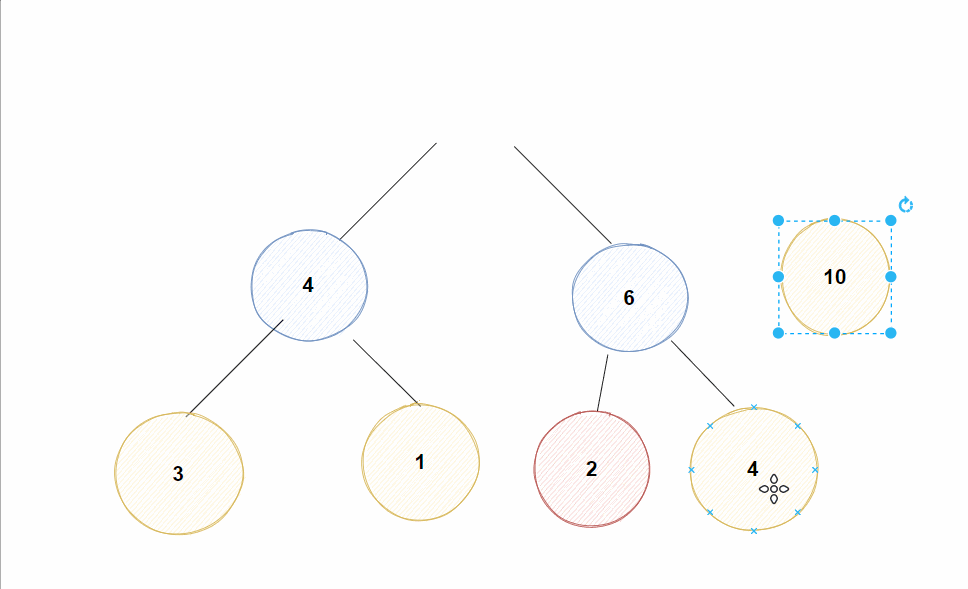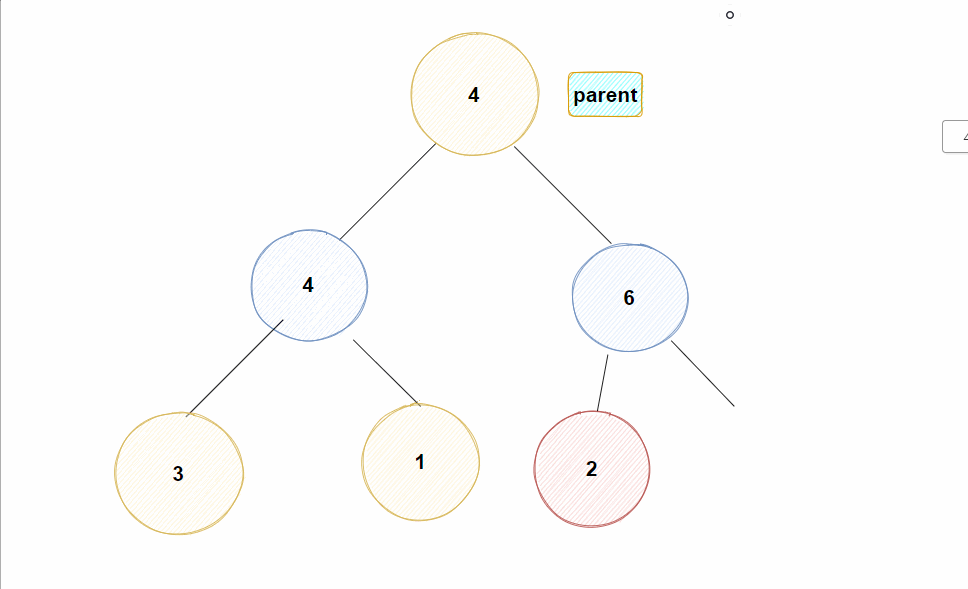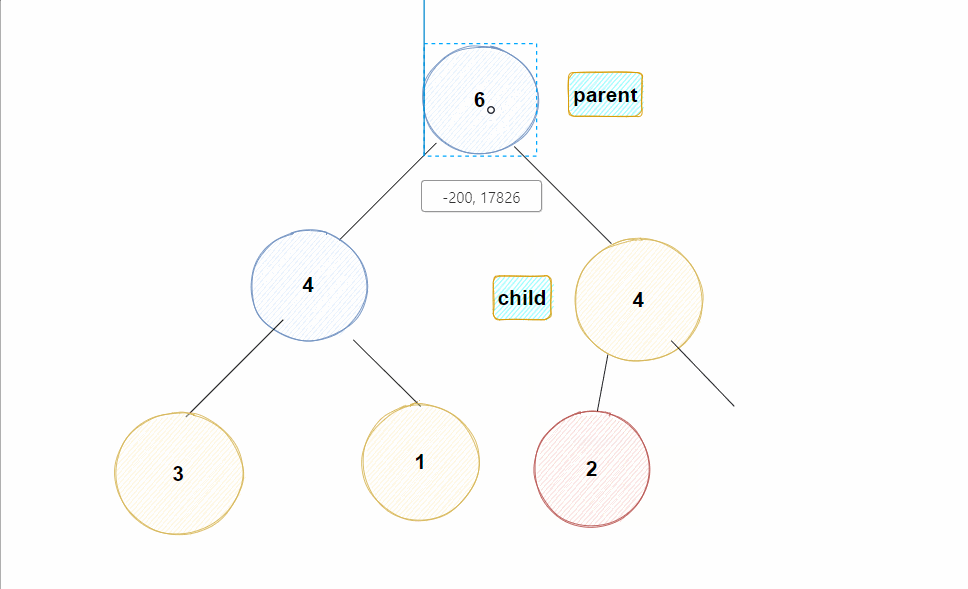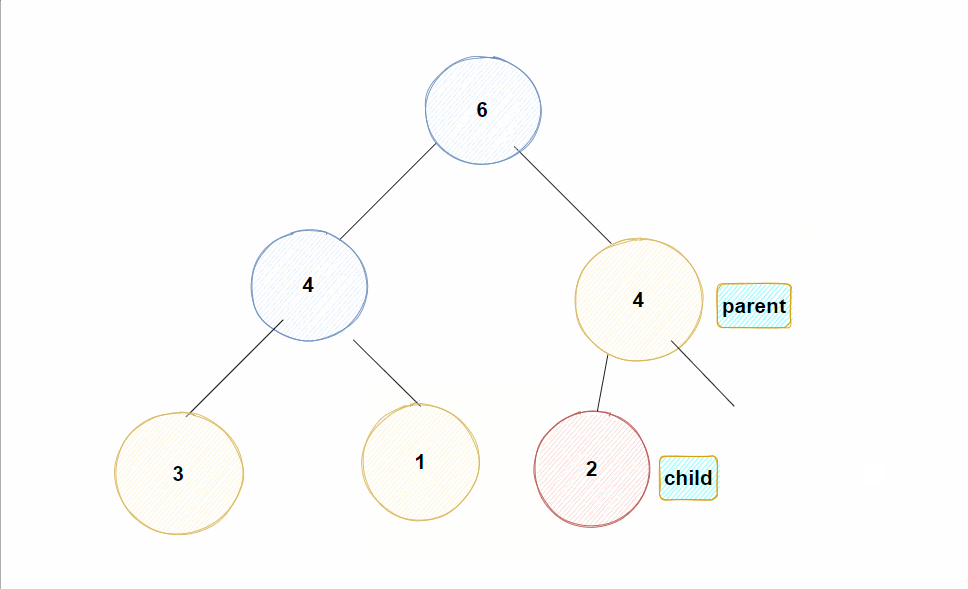
Eg： 假如现在对堆插入一个值为10的结点

✊动图示例：

1️⃣入堆的函数声明：

void HeapPush(HP* php, HPDataYtpe* x);

2️⃣入堆函数的实现：

void HeapPush(HP* php, HPDataYtpe* x)
{
	assert(php);
	//满了
	if (php->size == php->capacity)
	{
		//增容
		HPDataYtpe* tmp = realloc(php->a, php->capacity * 2 * sizeof(HPDataYtpe));
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity *= 2;
	}

	php->a[php->size] = x;
	php->size++;

	//向上调整算法
	Adjustup(php->a, php->size);
}

Ⅲ.删除堆顶数据

简单来说： 对堆顶删除一个元素

➡️实现： 即删除数组的第一个元素

❗特别注意：

• 如果直接删除堆顶的数据的，那就需要后面的整体数据往前挪动【$O(N)$】，并树的结构也发生改变，需要重新建堆【$O(N)$】，才能再次满足堆为大堆

• 那我们此时就可以先将堆顶和堆尾的值交换，并删除末尾的元素（因为已经交换了，所以到达删除堆顶元素的目的），最后再建堆一次即可【这样就比上面的方法少执行了$O(N)$次】

✊动图示例：

1️⃣出栈的函数声明：

void HeapPop(HP* php);

2️⃣出栈函数的实现：

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	Swap(php->a[php->size - 1], php->a[0]);
	// 交换到末尾后，删掉末尾数据【原堆顶】
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

Ⅳ.取堆顶数据

简单来说： 返回堆顶的数据

➡️实现： 即返回一个顺序表中第一个数据

❗特别注意：

• 需要判断顺序表此时是否为NULL（空表），如果是则不能返回了

1️⃣返回堆顶数据的函数声明：

HPDataYtpe HeapTop(HP* php);

2️⃣返回堆顶数据函数的实现：

HPDataYtpe HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

Ⅴ.判断堆是否为NULL

简单来说： 就是判断size是否为0

➡️实现： 因为size表示的是堆内的数据个数

• size为0，堆就为空

• 否则，堆为非空

1️⃣判断堆是否为NULL的函数声明：

bool HeapEmpty(HP* php);

2️⃣判断堆是否为NULL函数的实现：

bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

Ⅵ.获取堆内数据的个数

简单来说： 返回堆内数据个数

➡️实现： 返回size即可

1️⃣返回堆内数据个数的函数声明：

int HeapSize(HP* php);

2️⃣返回堆内数据个数函数的实现：

int HeapSize(HP* php)
{
	assert(php);

	return php->size;
}

Ⅶ.堆的销毁

简单来说： 对堆进行空间释放

➡️实现： 与顺序表的销毁操作一样

1️⃣堆的销毁的函数声明：

void  HeapDestroy(HP* php);

2️⃣堆的销毁函数的实现：

void  HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;

	php->capacity = php->size = 0;
}

Ⅷ.总结

✨综上：就是堆的接口实现的内容啦~

➡️相信大家对堆有不一样的看法了吧

---

总结

综上，我们基本了解了数据结构中的 “堆” 的知识啦~~

恭喜你的内功又双叒叕得到了提高！！！

感谢你们的阅读

后续还会继续更新，欢迎持续关注哟~

如果有错误❌，欢迎指正呀

✨如果觉得收获满满，可以点点赞支持一下哟~✨