Matching Net阅读笔记
Matching Net阅读笔记
Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. 2016: 3637-3645.
文章主要思想
本文主要解决的是FSL问题,但是本文的出现时间比MAML早,是Google DeepMind家的工作。本文主要受到2016年以前基于神经图灵机和Metrics Learning方法的影响,本文就从模型层面和训练过程做了一些工作,模型上,作者主要使用了基于attention和memory的网络结构,训练上作者接受传统机器学习的设定,将训练和测试阶段保持一致(在MAML那篇文章里我没有讲作者的为什么这么setup,个人认为有可能直接参照了这里的set)。
另一个作者contribution就是他们从ImageNet上提取出了更适合FSL问题的mini ImageNet数据集,不过这个感觉确实没什么技术含量哈哈哈哈。
Details
一些pre-knowledge
基于神经图灵机的方案主要是认为再FSL问题中,数据对于模型是insufficient的,所以NTM based方法希望通过强制神经网络去保存一些已知标注图像的特征信息(或者说是监督信息)来辅助后面的分类,所以神经图灵机的方法通常是使用了RNN族的结构加上一些extra memory slot,然后通过一些特定的策略去更新slot,这些策略包括但不限于为每个slot设定年龄,根据年龄更新slot,或者根据slot的使用情况、loss大小等等。但是这种方法严重依赖于人为提供的先验知识,如何设计规则也没有一个很好的方案。
Metrics Learning的方法就是老朋友了,主要思想是将图片或者文本从输入空间映射到另一个更以区分的高维空间,通过高维空间之间的距离度量来确定新样本的类别。这种方法主要的bottleneck有两个:一个是embedding learning的方法,大部分的工作是偏向于这个方向的,这篇matching net就是其中之一;另一个是度量方法,其实度量方法很多,比如直接计算cosine啊、L1、L2等等,但是这些传统的方法和深度学习的方法到底谁更强呢?所以有了Siamese。
方法细节
受NLP基于attention的seq2seq的启发,将原本的one shot learning task看成是一个set-to-set的框架,这句话怎么感觉有点耳熟,今年ECCV的DETR好像也有这句话哈哈哈,其实这里作者想的就是能够在不对网络结构做修改的情况下对未见过的类别生成测试标签,作者的做法是设定一个利用一个从Support Set输入空间 S = { ( x i , y i ) } i = 1 k S=\{(x_i, y_i)\}_{i=1}^k S={(xi,yi)}i=1k到输出空间 C S ( x ^ ) C_S(\hat{x}) CS(x^)的一个映射,这个参数映射实际上就是在给定预测样本和Support Set的情况下,该样本标签的分布 P ( y ^ ∣ x ^ , S ) P(\hat{y}|\hat{x}, S) P(y^∣x^,S),此处的P是一个神经网络结构。由此作者把前述思路表示成了下面的表达式:
y ^ = ∑ i = 1 k a ( x ^ , x i ) y i \hat{y}=\sum_{i=1}^{k}a(\hat{x}, x_i)y_i y^=i=1∑ka(x^,xi)yi
a是一种注意力机制,表达由 a ( ⋅ ) a(·) a(⋅)来度量预测样本和已知样本的注意力,直观上的理解就是给一个样本,我要去找到我本来的Support Set里见过的和这个样本最类似的,然后看这个最类似的label是啥,是不是有点metrics learning那味了。那现在剩下的问题就是采用什么注意力结构,这篇文章的思路是用了带有softmax的cosine相似度,感觉很简单,看看就能懂:
a ( x ^ , x i ) = e c ( f ( x ^ ) , g ( x i ) ) ∑ j = 1 k e c ( f ( x ^ ) , g ( x i ) ) a(\hat{x}, x_i)=\frac{e^{c(f(\hat{x}), g(x_i))}}{\sum_{j=1}^k {e^{c(f(\hat{x}), g(x_i))}}} a(x^,xi)=∑j=1kec(f(x^),g(xi))ec(f(x^),g(xi))
式子不解释了,很简单,不过注意到里面有两个函数 f ( ⋅ ) , g ( ⋅ ) f(·),\ g(·) f(⋅), g(⋅)这两个函数是用来将support set和预测样本进行embedding的方法作者把它叫做Fully Conditional Embedding,不知道怎么翻译,怎么理解这个Fully?作者认为每个元素的embedding应该由S中的所有元素来决定,同时对于给定的输入x的embedding,也应该和S有关,这个其实很直观,因为对于给定输入的样本,我们应该要考虑他的整体分布,他不是以单个个体的形式存在的。那么如何才能考虑到整个集合呢?
作者定义对于Support Set中的样本,采用双向的LSTM进行embedding,即 g ( x i , S ) = h ⃗ i + h ← i + g ′ ( x i ) g\left(x_{i}, S\right)=\vec{h}_{i}+\stackrel{\leftarrow}{h}_{i}+g^{\prime}\left(x_{i}\right) g(xi,S)=hi+h←i+g′(xi),其中 h i ← \stackrel{\leftarrow}{h_i} hi←和 h i → \stackrel{\rightarrow}{h_i} hi→都是隐层向量:
h ⃗ i , c ⃗ i = LSTM ( g ′ ( x i ) , h ⃗ i − 1 , c ⃗ i − 1 ) h ˉ i , c ← i = LSTM ( g ′ ( x i ) , h ˉ i + 1 , c ˉ i + 1 ) \begin{aligned} \vec{h}_{i}, \vec{c}_{i} &=\operatorname{LSTM}\left(g^{\prime}\left(x_{i}\right), \vec{h}_{i-1}, \vec{c}_{i-1}\right) \\ \bar{h}_{i}, \stackrel{\leftarrow}{c}_{i} &=\operatorname{LSTM}\left(g^{\prime}\left(x_{i}\right), \bar{h}_{i+1}, \bar{c}_{i+1}\right) \end{aligned} hi,cihˉi,c←i=LSTM(g′(xi),hi−1,ci−1)=LSTM(g′(xi),hˉi+1,cˉi+1)
其中 g ′ ( x ) g^{\prime}(x) g′(x)为初始的embedding或者特征向量,可以利用卷积网络来提取。通过这种方法我们就能够LSTM的记忆特性来保存整个S中存在的全局背景信息,那剩下的最后一个问题就是如何给Query Set的(说明一下,作者在文中把Query Set叫做Batch Set)预测样本加上S的背景信息了,它采用的方法是 f ( x ^ , S ) = attLSTM ( f ′ ( x ^ ) , g ( S ) , K ) f(\hat{x}, S)=\operatorname{attLSTM}\left(f^{\prime}(\hat{x}), g(S), K\right) f(x^,S)=attLSTM(f′(x^),g(S),K),其中K是处理的次数, f ′ ( x ) f^{\prime}(x) f′(x)同上面 g ′ ( x ) g^{\prime}(x) g′(x)的方法,这个AttensionLSTM的公式如下:
h ^ k , c k = LSTM ( f ′ ( x ^ ) , [ h k − 1 , r k − 1 ] , c k − 1 ) h k = h ^ k + f ′ ( x ^ ) r k − 1 = ∑ i = 1 ∣ S ∣ a ( h k − 1 , g ( x i ) ) g ( x i ) a ( h k − 1 , g ( x i ) ) = softmax ( h k − 1 T g ( x i ) ) \begin{aligned} \hat{h}_{k}, c_{k} &=\operatorname{LSTM}\left(f^{\prime}(\hat{x}),\left[h_{k-1}, r_{k-1}\right], c_{k-1}\right) \\ h_{k} &=\hat{h}_{k}+f^{\prime}(\hat{x}) \\ r_{k-1} &=\sum_{i=1}^{|S|} a\left(h_{k-1}, g\left(x_{i}\right)\right) g\left(x_{i}\right) \\ a\left(h_{k-1}, g\left(x_{i}\right)\right) &=\operatorname{softmax}\left(h_{k-1}^{T} g\left(x_{i}\right)\right) \end{aligned} h^k,ckhkrk−1a(hk−1,g(xi))=LSTM(f′(x^),[hk−1,rk−1],ck−1)=h^k+f′(x^)=i=1∑∣S∣a(hk−1,g(xi))g(xi)=softmax(hk−1Tg(xi))
带attention的LSTM为Support Set中不同的元素提供了不同的注意力。
实验
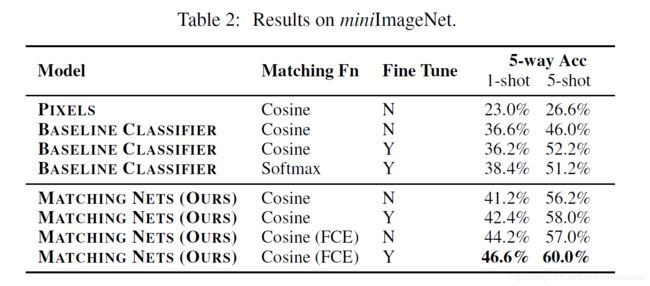
这是作者在Omniglot上的测试结果,其中,Pixel是指直接在raw Pixel上进行match(太顶了吧):
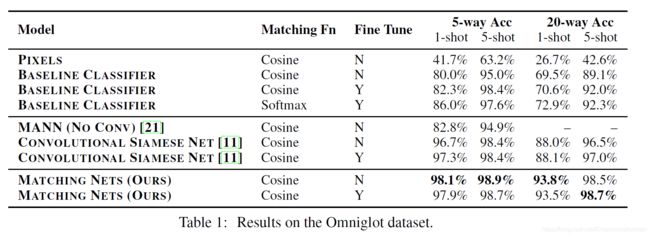
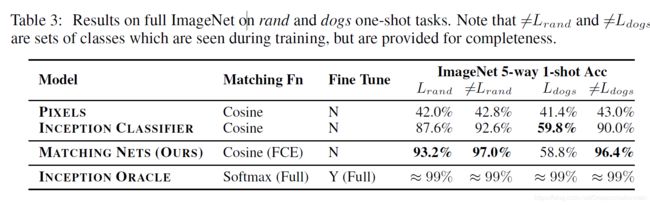
这是在整个ImageNet2012上对沙子和狗做one shot classification的结果:
My comment
回过头来再看看作者前面说的那个set to set问题,个人认为作者值得是embedding这里,每一个embedding是由整个上下文决定的,但是这种embedding应该也是经过pretrained的方式。从今天的角度看整个工作个人认为最大的亮点就在于在embedding的时候考虑了整个Support Set的影响,在实验结果上表现也较好,个人认为和LSTM的Pretrain有很大关系,同时作者进行度量的时候不是简简单单的采用一个cosine,而是一个带有softmax的cosine,不过有没有可能采用神经网络的方法来做metrics measure呢,可以的,马上就会写一篇2018年的工作,主要就是做这个的哈哈哈。
后记
这篇文章本来该昨天发的,但是昨天偷懒了哈哈哈,所以这篇写完了还要在整一篇relation net的哈哈哈哈哈,我太了,加油吧,打工人!另外,其实我这个是我自己的论文笔记,不是论文解读,所以可能有些地方有点晦涩,不过欢迎大佬一起交流或者指正。