TAML阅读笔记

TAML阅读笔记

Jamal M A, Qi G J. Task agnostic meta-learning for few-shot learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 11719-11727.

这篇TAML一看名字就知道是meta learning……他的这个名字太像MAML了哈哈哈，只不过MAML是Model Agnostic，这个TAML是Task Agnostic，这篇paper的作者华为云大佬齐国君也在知乎上写了文章讲这篇文章，大家可以去瞅瞅(题目是：任务无偏的元学习(Task-Agnostic Meta-Learning)：最小化任务性能之间的不平等)。这篇文章读的我是迷迷糊糊、懵懵噔噔，但是又感觉他的contribution很简单，去网上看了一些博客之后就差不多了，这里讲一讲我的一些理解。

一些pre-knowledge

照惯例，在讲这个之前我需要先将这篇文章中用到的一些先验知识讲清楚，这篇文章非常“有趣”的是他同时融入了信息论和经济学的知识……让我这个一直崇尚大道至简的人深感烦恼，心想我再也不会快乐了，快乐和我也没有什么关系。

熵

严格说来这都不算是需要讲的了，毕竟作为一个MLer，我想大家一定或多或少都有一些信息论的基础知识，知道熵是度量混乱程度的指标，也是度量不确定性的指标，我们这个世界总是自然的朝向熵增的方向发展……呸，走偏了，虽然大家可能都对熵有一些了解，不过这里我还是想对这一部分内容做一些简单的陈述。
首先说说自信息这个概念，自信息是用于单一事件发生时信息量的多少，简单来说自信息可以理解为事件对于观察者的判断的帮助大小，如果我对我同学说，你是一个人，拿这句话对他判断他今天中午吃什么没有任何帮助，我说的“你是一个人”这句话的信息量为0，因为她并没有改变任何我同学对于中午吃什么的不确定性。对于一个事件发生的概率越大，那么这个事情的不确定性就越小，他所携带的信息量就越少，即自信息越小。也就是说自信息和事件发生概率是成负相关关系，事件的不确定性和事件发生的概率成负相关关系。

那怎样去量化信息呢，按照现代科学的基本方法就是找参照物，我们找一个我们已知不确定性的事件作为参照，去衡量其他事件的不确定性，我们找的事件是抛硬币。抛一枚硬币可能的情况有两种，其不确定性我们定义为一个比特，抛两枚硬币可能的情况有四种，那就是两个比特，抛三枚硬币可能的情况有八种，那就是三个比特……所以如果我们要把抛硬币这个事件作为不确定性的度量的时候，它是以指数爆炸形式进行不确定性增加的，那对于一个事件相对于抛硬币的不确定性就应该是$2^n$比特，其中n是该事件相对于抛一个硬币的不确定性的大小，反过来n就等于$lo{g}_{2}m$，m是该事件的不确定性，这个不确定性m就是自信息；但是扔硬币的事件发生概率是均等，如果我们这个事件本身的概率值并不相等，比如张三李四王二麻子四个人打麻将，这几个人今天的手气肯定不一样了，假设他们四个赢的概率分别为0.1，0.2，0.3，0.4，那么最终这个麻将局的结果怎么计算，那就应该是他们四个的概率乘以他们本身的不确定性嘛，那也就是在求自信息的期望咯，这个期望我们就把它叫做信息熵。那问题来了，怎么样去测量这个自信息的大小，我们回过头来看看前面用的概率，概率0.1就是$\frac{1}{10}$，也就是在10个等概率事件中发生一次的概率，这个10就是发生的不确定性的数量，也就是这个m等于概率的倒数。至此我们有了自信息的表达式：$$I(x)=\log \frac{1}{P(x)}$$
根据分析，熵就是自信息的期望即：$$\begin{array}{rl}H[x]& =E_{x\sim p}[I(x)]=-E_{x\sim p}[\log p(x)]\\ & =-\sum _{x}p(x)\log p(x)\\ & =-\int p(x)\log p(x)dx\end{array}$$
熵越大，变量的取值越不确定，反之就越确定。

由定义，当信息被拥有它的实体传递给接收它的实体时，仅当接收实体不知道信息的先验知识时信息才得到传递。如果接收实体事先知道了消息的内容，这条消息所传递的信息量就是0。只有当接收实体对消息对先验知识少于100%时，消息才真正传递信息。

而对于两个随机变量之间的距离我们称为相对熵，更出名的名字叫KL散度，记为$D_{KL}(p\Vert q)$，其计算公式为：$$D(p\Vert q)=\sum _{x}p(x)\log \frac{p(x)}{q(x)}=E_{p(x)}\left(\log \frac{p(x)}{q(x)}\right)$$，虽然说KL散度是在衡量距离，但是KL散度不对称，也就是$D_{KL}(p\Vert q)\ne D_{KL}(q\Vert p)$，在信息论中，KL散度实际表示的是用分布 P 的最佳信息传递方式来传达分布 Q，比用分布 Q 自己的最佳信息传递方式来传达分布 Q平均多耗费的信息长度，衡量的是两个分布之间的差异。

而用分布P 的最佳信息传递方式来传达分布Q 中随机抽选的一个事件所需的平均信息长度为交叉熵，在神经网络(机器学习)中作为损失函数，而且通常是用作分类问题的损失函数，用来衡量两个随机变量之间的相似度。记作：
$$\mathrm{H}(\mathrm{p},\mathrm{q})=\sum _{i}p(i)\cdot \log \left(\frac{1}{q(i)}\right)$$

不平等性度量

这个不平等性度量是经济学里的，mmp我觉得我实在不想去看这个了，我干脆直接把这些指标拿出来：

1. 广义熵指数：是对收入不平等的一种度量。
2. 戴尔指数：戴尔指数主要是利用信息论中的资讯熵的概念导出的。戴尔指数等于资讯冗余，也就是资料最大可能资讯熵减去观测到的资讯熵，它是广义熵指数的特例，可以被视为冗余度、单样性、不平等、非随机性和可压缩性的度量。
3. Gini系数：总算听到一个比较熟悉的名词了。是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标，其中收入基尼系数具体含义是指，在全部居民收入中，用于进行不平均分配的那部分收入所占的比例。
4. 对数方差：直白的意思，就是值先求其对数再求方差用于衡量不平等。
5. 阿特金森指数是测度收入分配不公平指数中明显带有社会福利规范看法的一个指数。

如果上面的几个系数你看不懂我觉得也没关系，反正我也看不懂，但是只要知道它可以衡量不平等的程度就可以了。

文章主要思想

说了一大堆，回到本文中来，本文是在讨论一个什么事情呢？我们知道元学习的目的是通过元训练阶段获得一个meta learner能够给新的任务产生较好的初始参数，前面的文章我们分析过，参数初始化是会严重影响模型的训练的，不合理的参数初始化很可能导致模型陷入一个局部最优。在这一方面MAML的表现是非常优秀的了，但是其实meta learning本身就是在给定样本下训练的，他就有可能更偏向于与训练任务的相似的新task，最终直接影响模型的泛化能力，这就是作者的名字的由来，他希望搞一个模型是对所有任务的都没有偏差的，基于MAML的meta learning方法。这里引用作者在知乎的博客的原话：

具体来说，对训练一个元学习(meta-learner)模型而言，我们需要多个训练任务。尽管meta-learner会通过最小化更新后的模型在训练任务上的验证误差来训练meta-learner，但我们没有办法保证meta-learner训练出来的初始模型参数对所有任务都是没有偏差的。

一个很可能发生的情形是，初始模型对某些任务跟有效，而对另外一些任务就不是特别有效。这种情形，我们称meta-learner对不同任务是有偏的。一个有偏的meta-learner，在未来会遇到的新任务上，就有很可能不能给出一个很好的初始模型参数，而从使得从这个初始点开始，对模型进行有效的快速更新。

——齐国君

Details

这里作者给了两种思路，第一种是对一个分类任务，我们可以直接最大化初始模型在不同类别上的熵（Entropy Maximization）来实现对任务的无偏性。在讲之前我们先定义一下对于单个任务的熵：
$${\mathcal{H}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)=-{\mathbb{E}}_{x_i\sim P_{{\mathcal{T}}_i}(x)}\sum _{n=1}^N{\hat{y}}_{i,n}\log \left({\hat{y}}_{i,n}\right)$$

其中，$f(\theta )$表示初始模型，$y_i$表示输出，N是样本数量。我们希望meta learner对每一个任务都要unbias，熵越大则表明预测结果随机性越高，从上面对熵的定义来说，就是最大化不确定性，也就是最大化这个熵。注意这里是$f(\theta )$，是初始模型，$f({\theta }_i)$表示的是训练之后的模型，我们的目的又是要使得训练之后的模型的熵最小，这是机器学习的定义，那么我们的工作就是$min{\mathcal{H}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i}\right)$和$max{\mathcal{H}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)$，把他们俩整合一下都做成最小化的形式再将其与元训练目标结合起来得到以下目标函数就有了：
$$\underset{\theta }{\min }{\mathbb{E}}_{{\mathcal{T}}_i\sim P(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i}\right)+\lambda \left[-{\mathcal{H}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)+{\mathcal{H}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i}\right)\right]$$
然后将MAML的优化函数改成这就行。但是我们注意到i我们这里用的交叉熵，但是交叉熵适用的对象是分类任务啊，对于其他任务咋办？请看思路二。

---

另一个思路就是枪打出头鸟，我用一个不平等的度量来刻画meta-learner 在不同任务的bias。这里就用到上面提到的几个经济学里的指标，在原论文中有作者的公式，大家可以看看，我这里就简单的用${\mathcal{I}}_{\mathcal{E}}\left(\left\{{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)\right\}\right)$来表示，那么我们就直接在强化学习或者回归任务的目标函数上加上这个正则项，来惩罚那些收入比较高的。“婷婷”，啥是这些任务的收入？对于每个任务的损失函数来说，负损失就相当于每个任务的收入，所以最终的目标函数就变成了：

$${\mathbb{E}}_{{\mathcal{T}}_i\sim p(\mathcal{T})}\left[{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i}\right)\right]+\lambda {\mathcal{I}}_{\mathcal{E}}\left(\left\{{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)\right\}\right)$$

其算法的流程如图，其主要的改变就是在我框起来那部分的参数更新上：

My comment

觉得还是有必要再把MAML的算法自己写一下，感觉刚开始读这篇论文的时候很多地方都不懂，不得不再把MAML翻出来又反复的看了看。这篇文章其实为了达到这个任务无偏主要思想就是通过加正则项来促进目标函数对与任务偏好的惩罚，文章的思路感觉还是很清晰，但这种跨领域交叉太强了，不愧是华为的大佬哈哈哈。但是这篇文章同样没有解决MAML的model structure必须相同的问题。同时作者在论文中也对强化学习进行了实验，实验效果也很不错。

结果

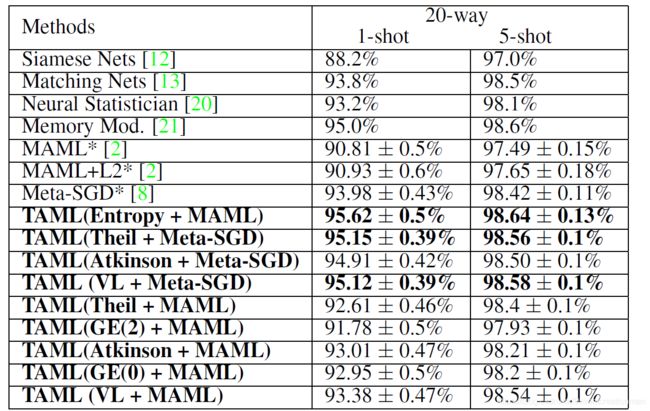
贴一贴实验结果，这是在Omniglot上20way的结果：

Future Work

想法

哈哈哈，这是前天的论文哈哈哈，昨天的论文还没看懂，明早起来再看看……

如果你觉得我的文章写的不错的话，麻烦帮忙向大家推广关注我的公众号啊（名称：洋可喵）！！！