模拟退火算法求解TSP问题(python)
TSP旅行商问题
旅行商问题大家都应该非常熟悉了,解法也很多,比如贪婪算法、Dijkstra算法等等,本文参考《MATLAB智能算法30个案例分析(第2版)》中第19章的内容,利用模拟退火算法求解TSP问题并给出了python实现版本
TSP问题描述如下:

TSP模拟退火算法
关于模拟退火算法的原理,书籍和文章均比较多,这里就不再赘述,大家可以参考其他博文,或阅读《MATLAB智能算法30个案例分析(第2版)》这本书。
程序及运行结果(笔者python环境为3.7)
import copy
import math
import random
import matplotlib.pyplot as plt
# 初始温度
T0 = 1000
# 终止温度
Tend = 1e-3
# 个温度下的迭代次数(链长)
L = 200
# 降温速率
q = 0.9
# 各个城市的坐标
X = [(16.4700, 96.1000),
(16.4700, 94.4400),
(20.0900, 92.5400),
(22.3900, 93.3700),
(25.2300, 97.2400),
(22.0000, 96.0500),
(20.4700, 97.0200),
(17.2000, 96.2900),
(16.3000, 97.3800),
(14.0500, 98.1200),
(16.5300, 97.3800),
(21.5200, 95.5900),
(19.4100, 97.1300),
(20.0900, 92.5500)]
# 构建距离矩阵
def build_distance():
# 初始化城市距离矩阵
distance = [[0 for _ in range(len(X))] for _ in range(len(X))]
# 计算各个城市之间的距离
for i in range(len(X)):
pos1 = X[i]
for j in range(i+1, len(X)):
pos2 = X[j]
distance[i][j] = pow((pow(pos1[0] - pos2[0], 2) + pow(pos1[1] - pos2[1], 2)), 0.5)
distance[j][i] = distance[i][j]
return distance
# 产生新的路径解
def gen_new_path(path):
new_path = copy.copy(path)
# 随机产生两个索引
idx1 = random.randint(0, len(path) - 1)
idx2 = random.randint(0, len(path) - 1)
# 交换路径中的两个城市
temp = new_path[idx1]
new_path[idx1] = new_path[idx2]
new_path[idx2] = temp
return new_path
# 计算路径总距离
def path_distance(path, distance):
total_distance = 0.0
# 循环路径上所有城市进行计算,到最后一个城市返回出发城市
for i in range(len(path)):
if i == len(path) - 1:
total_distance += distance[path[i]][path[0]]
else:
total_distance += distance[path[i]][path[i + 1]]
return total_distance
# Metropolis准则函数
def metropolis(old_path, new_path, distance, t):
# 路径的能量即路径上各城市距离之和
# 新路径的能量函数和旧路径的能量函数之差
delta = path_distance(new_path, distance) - path_distance(old_path, distance)
# 若新路径能量低于旧路径,则接受新路径解
if delta < 0:
return copy.copy(new_path), path_distance(new_path, distance)
# 若新路径能量高于旧路径,则按exp(-delta/t)概率接受新路径解
if math.exp(-delta/t) >= random.uniform(0, 1):
return copy.copy(new_path), path_distance(new_path, distance)
# 不接受新路径解
return copy.copy(old_path), path_distance(old_path, distance)
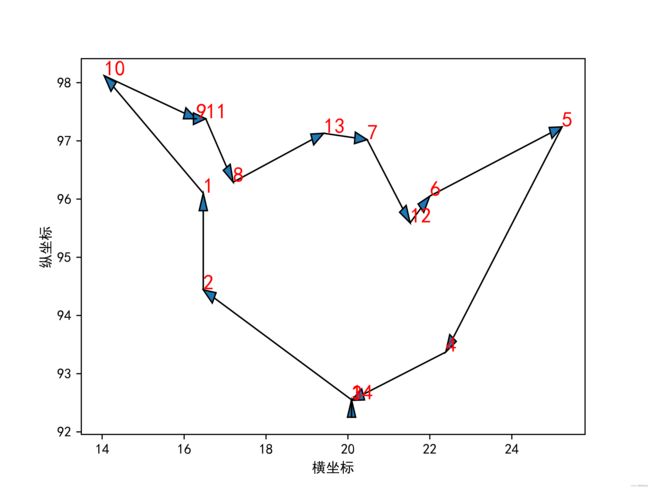
# 绘制结果
def draw_result(best, file_name="tsp_sa"):
# 各个城市的横纵坐标
x = [pos[0] for pos in X]
y = [pos[1] for pos in X]
# 绘图中文设置
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False
# 清空画布
plt.clf()
# 绘制箭头
for i in range(len(X)):
# 箭头开始坐标
start = X[best[i]]
# 箭头结束坐标
end = X[best[i + 1]] if i < len(best) - 1 else X[best[0]]
plt.arrow(start[0], start[1], end[0] - start[0], end[1] - start[1], head_width=0.2, lw=1, length_includes_head=True)
# 绘制城市编号
for i in range(len(X)):
plt.text(x[best[i]], y[best[i]], "{}".format((best[i] + 1)), size=15, color="r")
plt.xlabel(u"横坐标")
plt.ylabel(u"纵坐标")
plt.savefig(file_name + ".png", dpi=800)
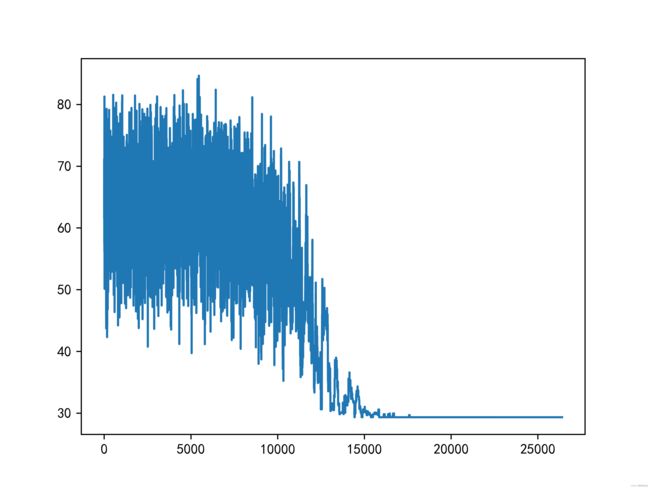
# 绘制进化过程
def draw_evolution(evolution):
x = [i for i in range(len(evolution))]
# 清空画布
plt.clf()
plt.plot(x, evolution)
plt.savefig('tsp_sa_evolution.png', dpi=800)
# 模拟退火算法
def simulated_annealing():
# 城市距离矩阵
distance = build_distance()
# 城市个数
city_cnt = len(distance)
# 初始化城市路径,这里可以随机生成,也可以跟书中的初始路径保持一致
# path = random.sample(range(0, city_cnt), city_cnt)
path = [10, 13, 2, 8, 5, 3, 12, 6, 7, 0, 11, 4, 1, 9]
# 绘制初始路径
draw_result(path, "init_path")
# 初始路线长度
total_distance = path_distance(path, distance)
print("初始路线:", [p + 1 for p in path])
print("初始总距离:", total_distance)
# 温度
t = T0
# 进化过程,每一次迭代的路径总距离
evolution = []
# 循环直到冷却后停止
while t > Tend:
for _ in range(L):
# 产生新路径
new_path = gen_new_path(path)
# 更新最佳路径及对应的距离
path, total_distance = metropolis(path, new_path, distance, t)
# 更新进化过程
evolution.append(total_distance)
# 降温
t = t * q
# 打印退火后信息
print("结束温度为:", t)
print("最佳路线:", [p + 1 for p in path])
print("最佳距离:", total_distance)
# 绘制最佳路径
draw_result(path, "tsp_sa_best")
# 绘制进化过程
draw_evolution(evolution)
if __name__ == "__main__":
simulated_annealing()
程序打印信息如下:
初始路线: [11, 14, 3, 9, 6, 4, 13, 7, 8, 1, 12, 5, 2, 10]
初始总距离: 56.0122140089359
结束温度为: 0.0009120344560464498
最佳路线: [14, 2, 1, 10, 9, 11, 8, 13, 7, 12, 6, 5, 4, 3]
最佳距离: 29.340520066994227
笔者水平有限,若有不对的地方欢迎评论指正