模拟退火求解TSP附python源码

1 模拟退火算法

1.1 算法流程

Step1 初始化：设定初始温度$T_0$，每个温度下的迭代次数L，给定初始解M，终止条件(温度下限)；

Step2: 产生新解$M_c$;

Step3: 计算增量$\Delta T=C(M_c)-C(M)$;(其中$C(M)$为评价函数，TSP问题评价函数为路径里程)

Step4:若$\Delta T<0$则接受$M_c$成为新解，否则以$exp(-\Delta T/T)$的概率接受$M_c$作为新的当前解;

Step5:当算法满足要求或者达到终止条件，程序结束。

1.2 生成新解

产生新解的方式和禁忌搜索算法中生成邻域候选路径的方式一样，如下：

对当前回路R随机选取两个点，倒置两点之间所有点的顺序，形成候选回路cand_route

例：当前路径R =【1、5、6、4、2、3、7、1】，随机选取的两个点如【3,5】

则新的路径NR为：

• 代码实现

def random_swap_2_city(route):
    '''
    随机选取两个城市并将这两个城市之间的数据点倒置,生成新的回路
    '''
    new_route = route[:]
    index = sorted(random.sample(indexs,2))
    L = index[1] - index[0] + 1
    for j in range(L):
        new_route[index[0]+j] = route[index[1]-j]
    return new_route

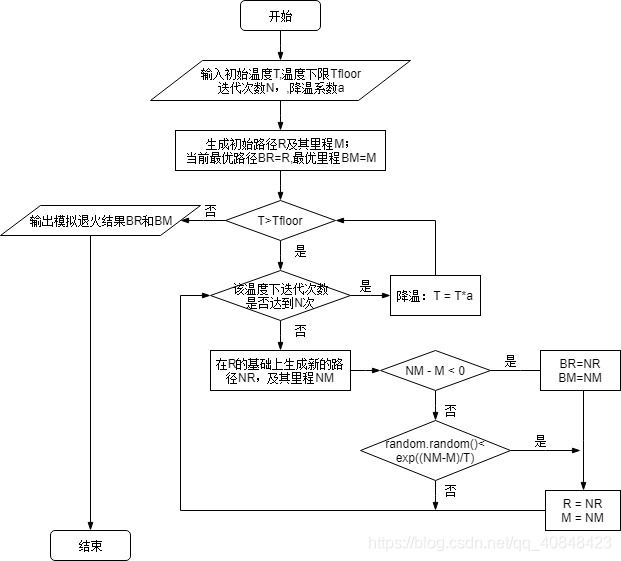
1.3 主函数

• 流程图

• 代码实现

def main():
    T=3000 #初始温度
    Tfloor=1 #温度下限
    alpha=0.995 #降温系数
    iter_count=100 #每一温度下的迭代次数
    route = city_num[:]
    random.shuffle(route) #随机生成初始解
    mile = route_mile_cost(route)
    # route,mile = greedy_initial_route(remain_cities) #贪婪算法形成初始解
    best_route,best_value = route[:],mile
    record = [best_value] #记录温度下降对应的当前解
    while T > Tfloor:
        for i in range(iter_count):
            cand_route = random_swap_2_city(route)#生成新的路径
            cand_mile = route_mile_cost(cand_route) #计算新路径的里程
            if cand_mile <= mile: #如果候选解比当前最优解更优则更新当前最优解
                route = cand_route[:]
                mile = cand_mile
                best_value = mile 
                best_route = route
                # T -= mile - cand_mile
            else: #如果候选解比当前最优解差，则按概率接受候选解
                p = math.exp((mile - cand_mile)/T)
                if random.random() < p:
                    route = cand_route[:]
                    mile = cand_mile
        T *= alpha #降温
        record.append(best_value)
    best_route = [origin] + best_route + [origin]
    return best_route,best_value,record

• 绘图函数

def fig():
    time_start = time.time()
    satisfactory_solution,mile_cost,record = main()
    time_end = time.time()
    time_cost = time_end - time_start
    print('time cost:',time_cost)
    print("优化里程成本:%d" %(int(mile_cost)))
    print("优化路径:\n",satisfactory_solution)
    #绘制路线图
    X = []
    Y = []
    for i in satisfactory_solution:
        x = city_location[i-1][0]
        y = city_location[i-1][1]
        X.append(x)
        Y.append(y)
    plt.scatter(x,y)
    plt.plot(X,Y,'-o')
    plt.title("satisfactory solution of TS:%d"%(int(mile_cost)))
    plt.show()
    #绘制迭代过程图
    plt.xlabel('温度变化',fontproperties="SimSun")
    plt.ylabel('路径里程',fontproperties="SimSun")
    plt.title("solution of SA changed with temperature")
    plt.plot(record,'-')
    plt.show()

2 算例分析（以berlin52为例）

2.1 探究初始解对SA求解结果的影响

在其他条件相同的情况下，调整初始解的生成方式，重复实验10次，SA结果如下图所示

结果分析:初始解的好坏对本实验所用SA并无太大影响，贪婪算法求得初始解后再进行模拟退火运算的结果反而比随机生成初始解模拟退火的结果要差，前者更加容易陷入局部最优。对berlin52算例而言，初始解随机下退火10次结果达到参考解7544的有6次，可见SA算法还是比较可观的。

2.2 探究初始温度对算法结果的影响（以下分析初始解均是随机生成）

通常情况下初始温度越高的话，SA求得的解应当更好。但在本次实验中，得出了相反的结果。初始温度1000反而比2000和3000下SA求得的结果更好，这可能是因为实验次数较少。从实验结果看3种温度下都能够在较短时间内跑出最优解，并且在每组10次实验中得出的最优解次数还不少，可见SA算法对于求解小规模的TSP问题效果还是相当可观的。

2.3 探究降温系数对算法结果的影响

从以上三组不同降温下得出的平均gap可以看出，随着降温系数的降低（这意味着降温得越快），SA结果越偏离最优值，当降温系数为0.9时（如果当前温度为10度，那么一次降温后的温度降温9度，可见降温速度之快），在改组10次实验中没有求得最优值，而0.99和0.995两组均有求得最优值，且0.9这组数据下的均值显著高于0.995和0.99下的均值。虽然降温越快使得程序运行时间越快，但是求得的结果变差了。因此在采用SA算法时应适当注意降温系数的调整，降温不宜太快。

2.4 总结

SA求得的berlin52的最优路径

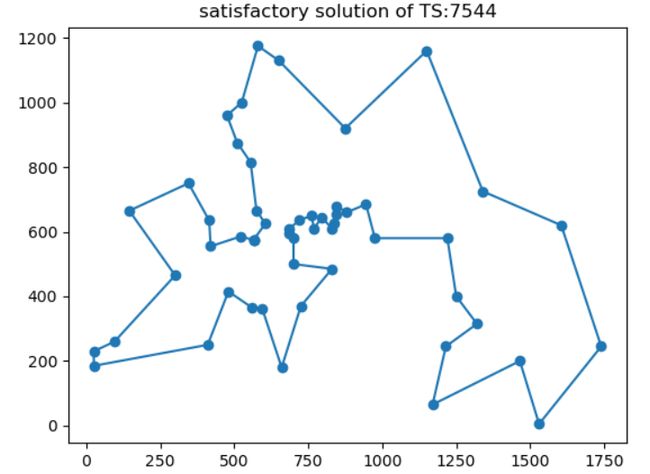
当前解随温度的变化过程，最终收敛到最优解7544。

如何在求解时间(程序运行时间）和求解效果(程序运行结果) 两者之间做好权衡是SA的一个重要问题。

此外，生成新解的方式对SA的表现至关重要。

3 附python源码(完整版)

import math,random,time
import matplotlib.pyplot as plt
#读取坐标文件
filename = '算例\\berlin52.txt' 
city_num = [] #城市编号
city_location = [] #城市坐标
with open(filename, 'r') as f:
    datas = f.readlines()[6:-1]
for data in datas:
    data = data.split()
    city_num.append(int(data[0]))
    x = float(data[1])
    y = float(data[2])
    city_location.append((x,y))#城市坐标

city_count = len(city_num) #总的城市数
origin = 1 #设置起点城市和终点城市
city_num.remove(origin)
remain_cities = city_num[:]  #迭代过程中变动的城市
remain_count = city_count - 1 #迭代过程中变动的城市数
#计算邻接矩阵
dis =[[0]*city_count for i in range(city_count)] #初始化
for i in range(city_count):
    for j in range(city_count):
        if i != j:
            dis[i][j] = math.sqrt((city_location[i][0]-city_location[j][0])**2 + (city_location[i][1]-city_location[j][1])**2)
        else:
            dis[i][j] = 0


def route_mile_cost(route):
    '''
    计算路径的里程成本
    '''
    mile_cost = 0.0
    mile_cost += dis[origin-1][route[0]-1]#从起始点开始
    for i in range(remain_count-1):#路径的长度
        mile_cost += dis[route[i]-1][route[i+1]-1]
    mile_cost += dis[route[-1]-1][origin-1] #到终点结束
    return mile_cost

#获取当前邻居城市中距离最短的1个
def nearest_city(current_city,remain_cities):
    temp_min = float('inf')
    next_city = None
    for i in range(len(remain_cities)):
        distance = dis[current_city-1][remain_cities[i]-1]
        if distance < temp_min:
            temp_min = distance
            next_city = remain_cities[i]
    return next_city,temp_min

def greedy_initial_route(remain_cities):
    '''
    采用贪婪算法生成初始解：从第一个城市出发找寻与其距离最短的城市并标记，
    然后继续找寻与第二个城市距离最短的城市并标记，直到所有城市被标记完。
    最后回到第一个城市(起点城市)
    '''
    cand_cities = remain_cities[:]
    current_city = origin
    initial_route = []
    mile_cost = 0
    while len(cand_cities) > 0:
        next_city,distance = nearest_city(current_city,cand_cities) #找寻最近的城市及其距离
        mile_cost += distance
        initial_route.append(next_city) #将下一个城市添加到路径列表中
        current_city = next_city #更新当前城市
        cand_cities.remove(next_city) #更新未定序的城市
    mile_cost += dis[initial_route[-1]-1][origin-1] #回到起点
    return initial_route,mile_cost

indexs = list(k for k in range(remain_count))
def random_swap_2_city(route):
    '''
    随机选取两个城市并将这两个城市之间的数据点倒置,生成新的回路
    '''
    new_route = route[:]
    index = sorted(random.sample(indexs,2))
    L = index[1] - index[0] + 1
    for j in range(L):
        new_route[index[0]+j] = route[index[1]-j]
    return new_route


def main():
    T=3000;Tfloor=1;alpha=0.995;iter_count=100
    route = city_num[:]
    random.shuffle(route)
    mile = route_mile_cost(route)
    # route,mile = greedy_initial_route(remain_cities)
    best_route,best_value = route[:],mile
    record = [best_value] #记录温度下降对应的当前解
    while T > Tfloor:
        for i in range(iter_count):
            cand_route = random_swap_2_city(route)
            cand_mile = route_mile_cost(cand_route)
            if cand_mile <= mile: #如果候选解比当前最优解更优则更新当前最优解
                route = cand_route[:]
                mile = cand_mile
                best_value = mile 
                best_route = route
                # T -= mile - cand_mile
            else: #如果候选解比当前最优解差，则按概率接受候选解
                p = math.exp((mile - cand_mile)/T)
                if random.random() < p:
                    route = cand_route[:]
                    mile = cand_mile
        T *= alpha #降温
        record.append(best_value)
    best_route = [origin] + best_route + [origin]
    return best_route,best_value,record
def fig():
    time_start = time.time()
    satisfactory_solution,mile_cost,record = main()
    time_end = time.time()
    time_cost = time_end - time_start
    print('time cost:',time_cost)
    print("优化里程成本:%d" %(int(mile_cost)))
    print("优化路径:\n",satisfactory_solution)
    #绘制路线图
    X = []
    Y = []
    for i in satisfactory_solution:
        x = city_location[i-1][0]
        y = city_location[i-1][1]
        X.append(x)
        Y.append(y)
    plt.scatter(x,y)
    plt.plot(X,Y,'-o')
    plt.title("satisfactory solution of TS:%d"%(int(mile_cost)))
    plt.show()
    #绘制迭代过程图
    plt.xlabel('温度变化',fontproperties="SimSun")
    plt.ylabel('路径里程',fontproperties="SimSun")
    plt.title("solution of SA changed with temperature")
    plt.plot(record,'-')
    plt.show()
    return mile_cost,time_cost
fig()
# R = 10
# Mcosts = [0]*R
# Tcosts = [0]*R
# for j in range(R):
#     Mcosts[j],Tcosts[j] = fig()
# AM = sum(Mcosts)/R #平均里程
# AT = sum(Tcosts)/R #平均时间
# print("最小里程:",min(Mcosts))
# print("平均里程:",AM)
# print('里程:\n',Mcosts)
# print("平均时间:",AT)