图像处理笔记——边缘检测算子

题目：下列图象边缘检测算子中抗噪性能最好的是︰（ ）
A. 梯度算子
B. Prewitt 算子
C. Roberts 算子
D. Laplacian 算子

边缘检测

直观来说，边缘是一区域内灰度值不连续或突变的地方。因此，边缘检测就是检测灰度值明显变化的区域，通常采用一阶导数（梯度计算）或二阶导数（拉普拉斯算子）的方法检测得到边缘。
如下图所示，分别给出了斜坡数字模型和基于它的灰度刨面图和一阶二阶导数刨面图。


在进入和离开斜面的变化点，一阶导数为正，在灰度级不变的区域，一阶导数为0；在边缘与黑色一边相关的跃变点二阶导数为正，在边缘与亮色一边相关的跃变点二阶导数为负，沿斜坡和灰度为常数的区域为0。
PS：另外，在讨论一阶和二阶微分过程中可以看到，沿着整个斜坡，一阶微分值都不为零，二阶微分值只有斜坡的初始点和终止点不为零，因此一阶微分产生较粗的边缘，二阶微分产生较细的边缘，且对细节有较强的响应（细节增强时，二阶微分效果往往更好）。同理，对于噪声，二阶微分比一阶微分的响应要强很多。此外，一阶微分处理一般对灰度阶梯有较强的响应，二阶微分处理对灰度阶梯变化产生双响应（正负值），在灰度值变化相似时，对线的响应要比对阶梯强，且点比线响应强。

回归正题，由上面两张图片可以得出结论，一阶导数可以用于检测图像中的一个点是否是边缘的点，二阶导数的符号可以用来判断一个像素点是在边缘亮的一边还是暗的一边。此外，二阶导数还有两条附加性质：1.对图像中每条边缘二阶导数生成两个值，一正一负（虽然并不希望有这个特点）；2.可以画出一条连接二阶导数正负极值的直线，在边缘中心附近穿过零点（前面说到，二阶微分会产生较粗的边缘线，一般将二阶导数过零点的点确定为边缘）。

确定边缘：一阶导数中，一个点的一阶导数大于阈值，就定义该点为边缘点；

二阶导数中，二阶导数的零交叉点即为边缘点。

梯度算子（一阶导数）

一幅数字图像的一阶导数是基于各种二维梯度的近似值，图像的梯度要基于在每个像素位置得到的偏导数。梯度算子一般分为水平方向和竖直方向。

Roberts
Roberts算子是最简单的一阶算子，又称为交叉梯度算子，通过局部差分计算检测边缘线条。

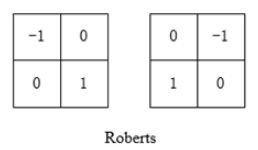
Roberts算子更注重于对角线方向，而忽视了水平和竖直方向的梯度变化，因此更容易检测出正负45度方向的边缘；此外，2x2大小的模板没有清楚的中心点，而且(x,y)点本身参加了梯度计算，不能有效的抑制噪声的干扰。适用于边缘明显或对角线方向且噪声较少的图像。

Prewitt
Prewitt提出来3x3大小的模板，模板区域内，第一行和第三行间的差近似于x方向上的导数，第三列和第一列的差近似于y方向上的导数。

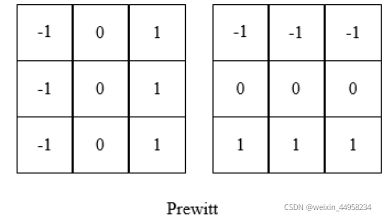
Prewitt算子类似于局部平均计算，(x,y)点本身不参加了梯度计算，对噪声有平滑作用，而且3x3的模板使其在水平和垂直方向的检测更加明显。适用于检测噪声较多，灰度渐变的图像。

Sobel
Sobel算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。

Sobel算子在Prewitt算子的基础上增加了权重的概念，认为相邻点的距离远近对当前像素点的影响是不同的，距离越近的像素点对应当前像素的影响越大，从而实现图像锐化并突出边缘轮廓（可以理解为增加中心点的重要性以实现某种程度的平滑效果）。Sobel算子的边缘定位更准确，当对精度要求不是很高时，可以提供较为精准的边缘方向信息。适用于检测噪声较多，灰度渐变的图像。

总结：以上所有模板中的系数总和为0，表示正如导数算子预示的，在灰度级不变的区域，模板响应为0。

此外，为了用于检测对角线方向，可以对Prewitt和Sobel算子进行调整，如下图所示。


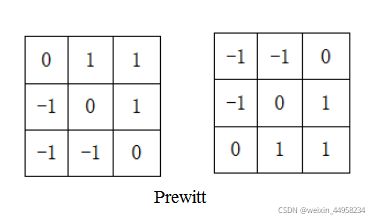
此外，虽然Sobel算子相对于Roberts和Prewitt算子来说，极大提高了抗噪能力，但依然没有彻底解决噪声污染的问题，同时检测出的边缘线依然比较宽。

二阶导数

二阶导数在分割中的作用主要包括：1. 利用零交叉性质进行边缘定位；2. 确定一个像素在一条边缘暗的一边还是亮的一边。
Laplacian 算子

拉普拉斯(Laplacian) 算子是维欧几里德空间中的一个二阶微分算子，常用于图像增强领域和边缘提取。它通过灰度差分计算邻域内的像素。拉普拉斯是一种微分算子，它强调图像中的灰度突变及灰度缓慢降低甚至消减的部分。

对于二维函数的拉普拉斯算子定义如下：

拉普拉斯数字实现用有两种实现：


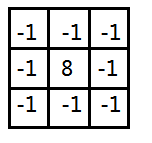
可以注意到，这两种模板分别对于90度和45度为增量的旋转变换是各向同性的，对于非水平和竖直方向的边缘也有较好的体现。另外，两模板之和均为0，也体现了在灰度级不变的区域，模板响应为0。

但上面已经提到过，二阶导数对噪声异常敏感，并且拉普拉斯算子的幅值会产生双边缘，且不能检测边缘的方向，因此一般不使用它的原始形式，而是考虑到拉普拉斯与平滑过程一起，先利用高斯型函数对图像进行平滑处理，减少图像本身的噪声影响和抵消二阶导数引起的噪声（主要作用），再利用拉普拉斯算子提供零交叉确定的边缘位置。由于二阶导数是线性运算，因此可以直接将高斯滤波与拉普拉斯算子结合高斯型的拉普拉斯算子的近似模板本质为：一个正的中心项，周围被一个相邻的负值区域围绕，并被一个零值的外部区域所包围。下图表示一个高斯型的拉普拉斯算子的近似模板。

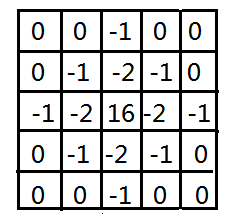
但它还是存在一些缺点，比如平滑掉了比较尖锐的边缘，造成无法检测到尖锐边缘的问题。

Canny算子

目前最常听到及最常用到的边缘检测算子应该是Canny算子，一种多级边缘检测算法。Canny算子检测效果比前面所讲的都要好一些，但实现起来麻烦一些。它的计算步骤如下：

step1：用高斯滤波器平滑图像；
step2： 计算图像中每个像素点的梯度强度和方向（用一阶偏导的有限差分来计算梯度的幅值和方向），类似于Sobel算子计算过程；
step3：对梯度幅值进行非极大值抑制（NMS），过滤掉非边缘像素，将模糊的边界变得清晰；
step4：用双阈值算法(Double-Threshold)检测来确定真实和潜在的边缘，通过抑制孤立的弱边缘最终完成边缘检测。

其中双阈值算法是Canny主要是因为非极大抑制后图像中仍然有很多噪声点。首先设定一个阈值上界和阈值下界，图像中的像素点如果大于阈值上界则认为必然是边界，称为强边界；小于阈值下界则认为必然不是边界，两者之间的则认为是候选项，称为弱边界。以强边界上的像素点为基础，不断在弱边界上搜索其8领域，当存在像素点时将其纳入，直至所有边界形成回路或访问结束。

Canny算子不容易受噪声干扰，得到的边缘精细且准确，缺点就是运算代价较高，运行于实时图像处理较困难，适用于高精度要求的应用。

总结

回归到一开始的题目，边缘检测中抗噪性能应该为：
Canny算子 > 一阶算子（梯度算子） > 二阶算子
其中一阶算子中： Sobel > Prewitt > Roberts

题目：下列图象边缘检测算子中抗噪性能最好的是︰（ ）
A. 梯度算子
B. Prewitt 算子
C. Roberts 算子
D. Laplacian 算子

所以答案为B。Laplacian 算子为二阶算子，效果最差；梯度算子包括所有一阶算子，包含B,C选项；Roberts 算子是梯度算子中抗噪性能最差的算子。

参考资料

数字图像处理:边缘检测(Edge detection)
数字图像处理(19): 边缘检测算子
数字图像处理（第二版）